基于匹配场处理的天波雷达高度估计算法

游 伟 何子述 胡进峰

(电子科技大学电子工程学院 成都 611731)

1 引言

天波高频超视距(Over-The-Horizon, OTH)雷达是一种具有超远距离目标探测和信息获取的雷达系统，其探测的目标通常是未知的和非协作的。天波 OTH雷达利用电离层对电磁波的反射、下视传播，实现对目标的检测和参数测量[1]。由于天波OTH雷达具有远程的探测能力，可以实现800-3500 km的海面特性、目标及海面上空目标进行探测，因此在国内外得到了广泛的研究和应用[2-10]。

天波雷达通常工作于高频段(3-30 MHz)，并采用距离-多普勒处理实现远距离目标的探测。距离多普勒处理可以估计得到目标的斜距和多普勒信息，而对于目标的高度信息则不能得到。高度信息作为目标的一个重要参数，对于目标的分类而言是非常关键的。比如在缉毒、走私、机场监测等应用中，就需要用到目标的高度信息。目前，基于天波雷达的目标高度估计算法研究公开的文献较少。

文献[11]提出一种超分辨算法来进行高度估计，其估计精度较低，只能区别高、中、低等3种等级，不能准确地获得目标的高度数据。而文献[12]则提出一种基于匹配场处理的算法。匹配场处理最早是在水声信号处理领域提出的。其物理意义是：利用已知或测量得到海洋环境参数和声信号在海洋环境中的传播信道特性，模拟得到相应的声场数据。将模拟得到的声场数据与实际观测的声场数据进行匹配处理，从而得到目标声源所在的真实距离和深度[13]。文献[12]将匹配场处理的概念引入到天波雷达的高度估计中，利用空中目标的微多径信号模型，将观测到的数据与根据微多径模型仿真出的数据进行匹配处理，并建立一阶马尔科夫概率模型。当观测数据的对数似然函数取得最大值时对应的目标高度即作为目标高度的最大似然估计。该算法假设模型中的复反射系数具有很好的预测性，因而稳健性较差。文献[14]则在文献[12]的基础上做了改进，对模型中的复反射系数所使用的一阶马尔科夫模型做了修正，得出了一种较为稳健的算法。

文献[12]和文献[14]都是利用多个驻留周期数据进行高度估计，其算法的思想都是建立观测数据的概率模型。而对算法的仿真研究表明，这样的处理算法稳健性较差，容易出现测高模糊。本文提出一种利用单个驻留周期数据进行目标高度估计的算法。该算法的思想仍然是基于匹配场的处理，首先分别对观测回波和模拟的回波数据协方差矩阵进行子空间分解，得到二者的信号子空间和噪声子空间。然后将仿真回波的信号矢量向回波的噪声子空间进行投影。当仿真的目标高度与实际目标高度匹配时，二者将实现正交。这样就可以得到目标的高度估计。

本文第2节给出了空中目标的微多径信号传输模型；第3节给出了目标高度估计算法；第4节给出仿真结果验证所提算法的有效性；第5节为全文总结。

2 信号模型

天波雷达要对目标进行探测，首先是向电离层发射高频信号，高频信号经过电离层反射后照射到海面的目标。目标的后向散射信号再投射到电离层并反射到雷达接收机。天波雷达采用双基的工作模式，双基雷达的俯视图由图1给出。如图1所示，设目标到发射机和接收机的地面距离分别是Dt和Dr，接收机与发射机间距为d，而目标相对于接收机的方位角为γ，根据上面的几何关系，发射机与目标距离的关系为

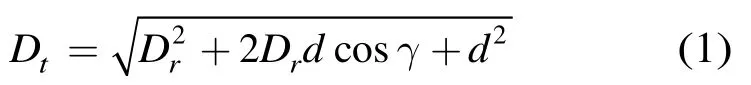
在目标到接收机的地面距离已知的条件下，可以根据式(1)得到目标到发射机的地面距离。

天波雷达发射波束在俯仰维有一定的宽度，因此，雷达发射的波束可以同时照射到一定距离范围内的目标。对于一个地面或海面目标，在单一电离层传播模式的情况下，仅有一条射线可以照射到该目标。同样，对于地面或海面的目标后向散射到接收机的射线，在单一电离层传播模式的情况下，也只有一条射线可以被接收机接收。而对于一个空中目标，由于目标存在一定的高度，雷达高频射线在被电离层反射后可能被海面或地面反射。这就使得空中目标与地面目标的回波具有不同的特点。

图1 双基雷达结构

为了说明问题，图2给出了空中目标局部的微多径示意图，其中实线代表发射射线(即从发射机发射，经过电离层反射后照射到目标)，而虚线代表接收射线(即是从目标后向散射，并被电离层反射后被接收机接收)。在考虑单一电离层传播模式及考虑地面或海面是镜面反射的条件下，雷达发射射线在经过电离层反射后有一条射线直接照射到该目标，同时也有一条射线经过地面或海面反射后照射到该目标。同样，对于目标的后向散射回波信号，接收射线可以直接回到电离层并被电离层反射到接收机，还有一条射线被地面或海面反射后进入电离层并被电离层反射，再被接收机接收。

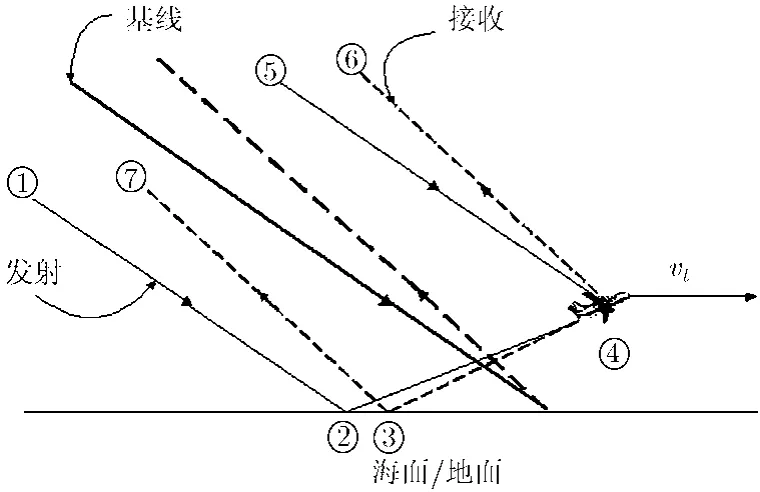
图2 天波雷达空中目标微多径模型

因此，信号从发射机照射到目标，再从目标后向散射到接收机一共有4条路径组合。如图2所示，这4条路径分别是：从电离层直接照射到目标，再从目标直接返回到电离层，即5-4-6路径(DD路径)；从电离层直接照射到目标，再从目标经过海面/地面反射回到电离层，即5-4-3-7路径(DD路径)；从电离层经过海面/地面反射照射到目标，再从目标直接返回电离层，即1-2-4-6路径(RD路径)；从电离层经过海面/地面反射照射到目标，再从目标经过海面/地面反射回电离层，即1-2-4-3-7路径(RR路径)。因此，当天波雷达照射到该空中目标后，目标的回波将是4条微多径信号的线性组合。确定4条微多径的斜距、多普勒频率、每条路径的反射系数，即可以确定该目标的回波。

天波雷达的信号传输需要经过电离层的反射，因此其传播的射线斜距、仰角与地面距离的关系与电离层模型有关。根据电离层多层抛物线(Multi-Quasi Parabolic, MQP)模型，射线的地面距离D及时延τ(对应于射线的斜距)与仰角的关系可以表达为[15,16]

利用目标的接收射线与发射射线的地面距离，结合电离层模型，就可以得到4条多径的射线仰角，其具体计算步骤为：(1)根据地面距离与射线仰角的关系，计算得到4条射线的仰角，设得到的4条射线的仰角分别为βt,d(发射的直接射线的仰角)，βt,r(发射的地面反射射线的仰角)，βr,d(接收的直接射线的仰角)，βr,r(接收的地面反射射线的仰角)。(2)得到4条射线的仰角后，利用射线延时与仰角的关系，计算得到射线的延时。记4条路径的延时分别为τt,d,τt,r,τr,d,τr,r。由于式(2)和式(3)都是复杂函数，不能得到显式的逆函数，因此，以上关系的求解都可以通过查表的方式进行。设目标径向速度为v，则目标在 4条射线方向的速度投影分别为vt,d=vcosβt,d,vr,d=vcosβr,d,vt,r=vcosβt,r及vr,r=vcosβr,r。可以根据以上关系得到4条射线的斜距和多普勒频率，如DR路径的斜距和多普勒频率可以写为

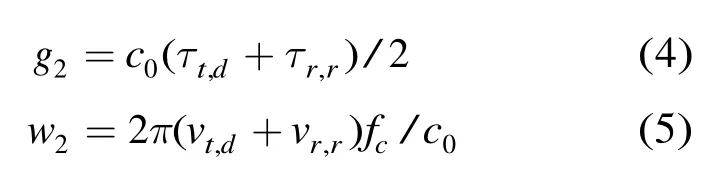
得到了目标的4条多径的距离和多普勒频率后就可以得到该目标的回波数据模型。对空中目标而言，其第k个扫描周期的回波数据可以写成矩阵形式。

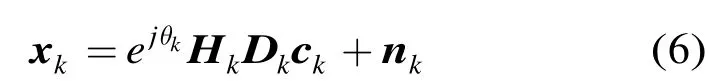
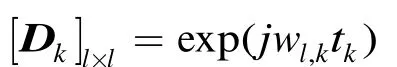
3 高度估计算法

文献[12]提出的高度估计算法将复反射系数建模为一阶 Markov模型，并利用多个驻留周期的数据进行联合处理，建立了关于高度的概率模型，最后对所得到的数据求解对数似然函数，似然函数最大处对应的高度便作为目标的高度估计。其算法可以表达为

其中xk为第k个驻留周期的观测数据，z为假设的目标高度，Δθk=θk-θk-1。对该算法的仿真研究表明，该算法稳健性较差。

本文提出一种更加稳健的算法，利用一个驻留周期的数据就可以估计出目标的高度。首先，对于第k个驻留周期的回波数据，其协方差矩阵可以写为

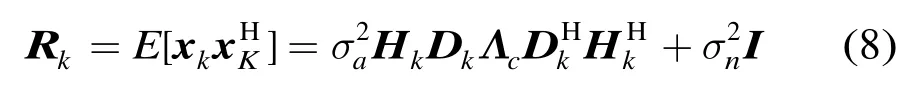
在实际使用中，由于4条路径的复反射系数是未知的，可以通过利用观测数据与仿真数据进行估计，其中，复反射系数及信号强度可以估计为

其中tr表示求矩阵的迹。

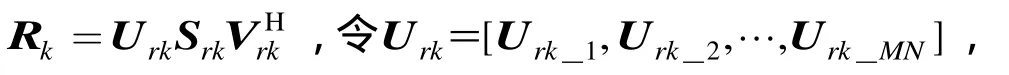
对于仿真数据，也利用式(8)对其协方差矩阵Rz进行估计，并对其做奇异值分析有Rz=UzSzVzH。设其最大奇异值对应的奇异矢量为Uz_1，则目标高度可以估计为

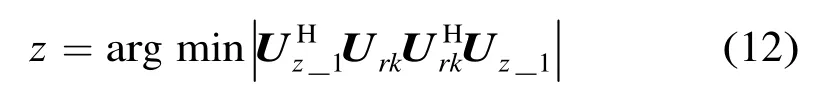
该算法主要利用观测数据与仿真数据协方差矩阵的子空间相似的特点，对观测数据与仿真数据分别进行子空间分解。当设定仿真的目标高度与实际目标高度匹配时，其子空间应该是最相似的，此时观测数据的噪声子空间应与仿真数据的信号子空间正交。在对观测数据求取协方差时，可以利用多个驻留周期的观测数据进行平均。

4 仿真结果

本节给出目标高度估计算法的仿真结果。仿真场景是飞机目标在雷达视线内以一定的高度飞行，经过天波雷达探测后，获得了该目标的地面距离和径向速度，现在要经过对该目标的连续观测获得该目标的高度信息。采用线性调频连续波(LFMCW)信号，主要的仿真参数如表1所示。另外，电离层采用3层电离层结构，分别为E,F1和F2层。采用文献[15]所给电离层参数，3层对地表的高度分别为120 km, 210 km, 320 km，厚度分别为20 km, 87 km,100 km，临界频率分别为3.0 MHz, 4.2 MHz, 6.0 MHz，并且假设电离层从F2层返回照射到目标。进行距离解调时，在距离维和多普勒维分别采用80 dB和70 dB的Chebyshev窗。在进行匹配场处理时，距离维取7点数据，而多普勒维取3点数据。这样的选取使得目标的微多径信息能够都包含在内。

表1 主要仿真参数

所得仿真结果分别由图3-图6给出。其中，图3给出了基于电离层模型所得到的空中目标4条多径的延时随其高度变化的曲线。图4给出目标4条多径的多普勒频率随其高度变化的曲线。从以上两图可以看出，目标4条多径的延时与多普勒频率的差别随着高度的增加而逐渐增加。然而其差别仍然很小使得目前天波雷达的分辨率还不能够将4条多径区分开。

图5和图6给出了算法估计得到的目标高度。其中图5给出了当目标高度为8000 m时的估计结果。可以看出，文献[12]所提算法的稳健性较差，其结果容易出现模糊，即该算法的对数似然函数容易在其它的高度上产生极大值。而本文算法的估计误差基本在2000 m左右。图6给出了当目标高度为12000 m时的高度估计结果。经过比较可以看出，本文算法比文献所提算法估计结果要好，而且本文算法稳健性更好。

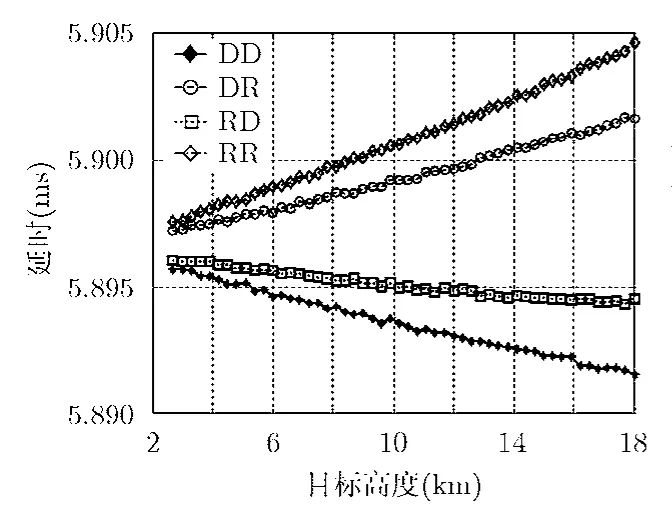
图3 4条路径延时随高度变化曲线

图4 4条路径多普勒频率随高度变化曲线

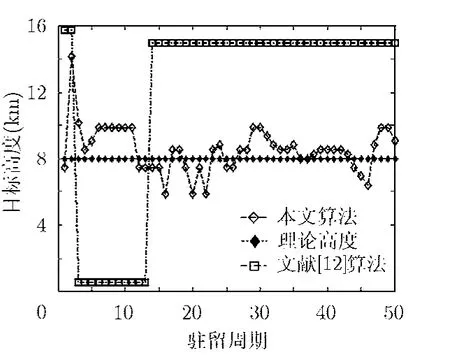
图5 目标高度为8000 m的估计结果

图6 目标高度为12000 m的估计结果

5 结束语

基于匹配场处理的理论，本文建立了空中目标微多径信号模型。利用空中目标观测回波数据协方差矩阵与仿真数据协方差矩阵子空间的相似性，提出一种比较稳健的目标高度估计算法。该算法只需要对协方差矩阵进行奇异值分解并进行子空间相关处理即可获得目标的高度参数。给出了仿真结果，仿真结果表明在给定的仿真场景下，所提算法估计误差在2000 m左右，比文献所提算法具有更好的稳健性。

[1]周文瑜, 焦培南. 超视距雷达技术[M]. 北京: 电子工业出版社, 2008: 1-38.

[2]周忠根, 水鹏朗. 基于复数据经验模式分解的天波超视距雷达瞬态干扰抑制[J]. 电子与信息学报, 2011, 33(12):2831-2836.

Zhou Zhong-gen and Shui Peng-lang. Transient interference suppression based on complex empirical mode decomposition in over-the-horizon radar[J].Journal of Electronics&Information Technology, 2011, 33(12): 2831-2836.

[3]姜维, 邓维波, 杨强. 高频超视距混合天地波雷达海杂波特点分析[J]. 电子与信息学报, 2011, 33(8): 1786-1791.

Jiang Wei, Deng Wei-bo, and Yang Qiang. Analyse of sea clutter for HF over the horizon hybrid sky-surface wave radar[J].Journal of Electronics&Information Technology, 2011,33(8): 1786-1791.

[4]全英汇, 张磊, 邢孟道, 等. 天波超视距雷达缺损信号的频谱重构[J]. 系统工程与电子技术, 2011, 33(8): 1732-1737.

Quan Ying-hui, Zhang Lei, Xing Meng-dao,et al.. Optimal reconstruction of spectrum with partial samples in OTHR[J].Systems Engineering and Electronics, 2011, 33(8): 1732-1737.

[5]周忠根, 水鹏朗. 基于小波影响锥的天波雷达瞬态干扰抑制方法[J]. 电波科学学报, 2011, 26(4): 688-692.

Zhou Zhong-gen and Shui Peng-lang. Transient interference excision based on wavelet influence cone in over-the-horizon radar[J].Chinese Journal of Radio Science, 2011, 26(4):688-692.

[6]周晨, 赵正予, 邓峰. 电离层行进式扰动对天波超视距雷达坐标配准的影响[J]. 系统工程与电子技术, 2011, 33(10):2222-2225.

Zhou Chen, Zhao Zheng-yu, and Deng Feng. Effects of the travelling ionospheric disturbance on skywave over-thehorizon radar coordinate registration[J].Systems Engineering and Electronics, 2011, 33(10): 2222-2225.

[7]刘慧霞, 梁彦, 陈绪元, 等. 一种自适应天波超视距雷达航迹融合算法[J]. 电子学报, 2009, 37(6): 1348-1352.

Liu Hui-xia, Liang Yan, Chen Xu-yuan,et al.. An adaptive OTHR multipath track fusion algorithm[J].Acta Electronica Sinica, 2009, 37(6): 1348-1352.

[8]金术玲, 梁彦, 潘泉, 等. 一种天波超视距雷达分级Hough变换航迹起始方法[J]. 电子与信息学报, 2008, 30(8): 1968-1972.

Jin Shu-ling, Liang Yan, Pan Quan,et al.. A two-hierarchy Hough transform based track initiation method for sky-wave over-the-horizon radar[J].Journal of Electronics&Information Technology, 2008, 30(8): 1968-1972.

[9]康蓬, 韩蕴洁, 卢琨, 等. 波束倾斜修正在天波超视距雷达中的应用[J]. 电波科学学报, 2009, 24(6): 1150-1153.

Kang Peng, Han Yun-jie, Lu Kun,et al.. Application of beam tilting correction in skywave over-the-horizon radar [J].Chinese Journal of Radio Science, 2009, 24(6): 1150-1153.

[10]Zhang Y, Frazer G J, and Amin M G. Concurrent operation of two over-the-horizon radars[J].IEEE Journal of Selected Topics in Signal Processing, 2007, 1(2): 114-123.

[11]Anderson C W, Green S D, and Kingsley S P. HF skywave radar: estimating aircraft heights using super-resolution in range[J].IEE Proceedings-Radar, Sonar and Navigation, 1996,143(4): 281-285.

[12]Papazoglou M and Krolik J L. Matched-field estimation of aircraft altitude from multiple over-the-horizon radar revisits[J].IEEE Transactions on Signal Processing, 1999, 47(4):966-976.

[13]杨坤德. 水声阵列信号的匹配场处理[M]. 西安: 西北工业大学出版社, 2008: 1-9.

[14]Anderson R H, Kraut S, and Krolik J L. Robust altitude estimation for over-the-horizon radar using a state-space multipath fading model[J].IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(1): 192-201.

[15]Papazoglou M. Matched-field altitude estimation for overthe-horizon radar[D]. Duke University, 1998.

[16]Dyson P L and Bennett J A. A model of the vertical distribution of the electron concentration in the ionosphere and its application to oblique propagation studies[J].Journal of Atmospheric and Terrestrial Physics, 1988, 50(3): 251-262.