一种快速精确设计滤波器型输出回路的新方法

曹 静 丁耀根 刘濮鲲

(中国科学院电子学研究所 中国科学院高功率微波源与技术重点实验室 北京 100190)

1 引言

速调管输出回路的输出间隙阻抗频率特性对速调管的效率、带宽等指标有重要影响。因此，关于加载滤波器的宽带输出回路的设计，主要是在要求的频带范围内获得满足一定波动要求的间隙阻抗频率特性[1,2]，同时获得该输出回路的3维几何结构尺寸。

许多文献报道了加载滤波器的宽带输出回路的设计、模拟方法以及冷测实验[1-6]，但上述传统的理论设计方法需通过查表[7]获得几何结构尺寸，存在一定的误差；文献[4-6]开展的计算模拟研究工作虽能在理论设计的基础上给出较精确的3维几何结构尺寸，但仍然无法避免面对电脑的人工调试的冗长过程。

本文提出的快速精确设计滤波器型输出回路的新方法仍然以文献[1-3]中的滤波器加载宽带输出电路的理论设计方法为基础和指导，充分利用3维软件中可设置“离散端口”以及可“自动优化”的功能，把繁琐，冗长的调试过程完全交给计算机完成，减少了人力物力，在很大程度上加快了速调管的研制进度，同时能获得精确的3维几何结构尺寸。

为了能更好的阐述新方法的设计过程以及比较传统设计方法和新方法的异同，分别列出它们的设计流程图。

从图1可知，无论冷测试验调试还是3维模拟调试，都存在“不合格”时的循环反复设计过程，同时这一过程需人工手动完成。而利用本文提出的新方法，如图2所示的流程可知，只需正确设置优化目标和优化参数，即可由计算机自动完成优化设计，获得精确的计算结果。

下面本文将详细阐述新方法的理论基础及如何完成设计流程中的各项步骤。

2 利用“驻波比方法”模拟设计滤波器型输出回路的理论及方法

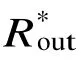
图1 传统方法设计滤波器型输出回路的流程

图2 新方法设计滤波器型输出回路的流程

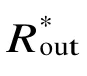
对于速调管，1 dB带宽是指输出功率电平大于最大输出功率电平的80%的频带宽度，根据输出功率电平与间隙阻抗实部R成正比的关系以及相对功率电平W与驻波比ρ的关系(W=4ρ/(ρ+1)2)，可有

式中Rmin表示带宽范围内阻抗实部最小值，Rmax表示带宽范围内阻抗实部最大值。阻抗波动1 dB时，

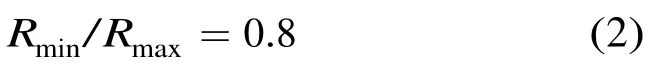
再根据驻波比ρ与反射系数T的关系：

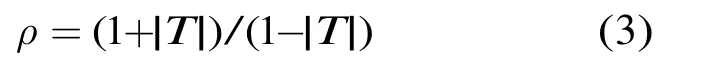
由式(3)可知，当反射系数T为绝对值相等的正负两个值时，可获得相同的驻波比。再由反射系数T与归一化阻抗z(z=R/zc,zc是特性阻抗)的关系：

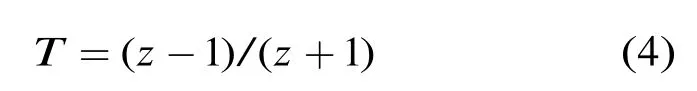
由式(3)和式(4)可知，会有两个归一化阻抗满足驻波比的要求，若设这两个阻抗为R1和R2，则可推导出R1和R2的关系为

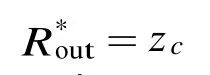
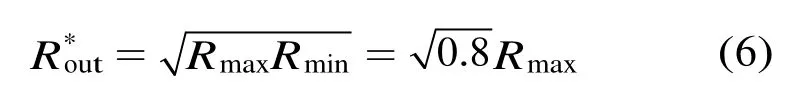
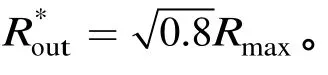
当然，若要设计间隙阻抗波动更大(例如3 dB)或更小(例如 0.5 dB)的滤波器型输出回路，仍可以根据本文上面的理论，求出间隙处接入的电阻及驻波比ρ的取值范围。

虽然计算机会自动存储一种参数组合，但在计算机获得所有计算结果中，在要求的带宽范围内，满足ρ的取值范围的参数组合不止一种，设计者也可根据需要从中选取。

3 利用“驻波比方法”模拟不加载滤波器的输出回路

为了验证上述理论的正确性及实用性，首先对一个单间隙腔与波导孔耦合形成的不加载滤波器的输出回路进行模拟，图3给出了利用CST微波工作室通过对单端口问题计算获得外观品质因数Qext与频率的关系曲线[8]，从而获得中心频率为2.5 GHz，外观品质数Qext=101。计算出该输出腔的特性阻抗R/Q=41，根据式(7)和式(8)[2]可获得该输出回路的1 dB带宽为 12.5 MHz以及最大间隙阻抗Rmax=4141 Ω。

图3 外观品质因数与频率关系曲线

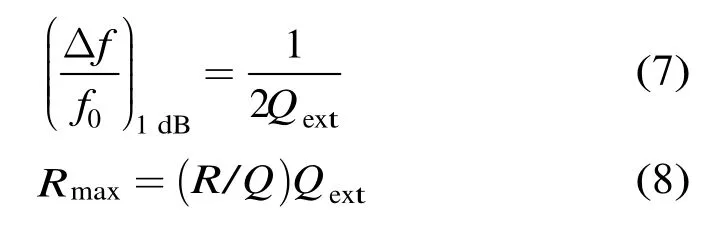
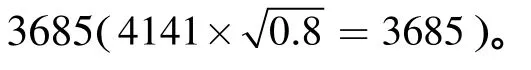
图4给出了从输出波导口向间隙看去的驻波比与频率的关系曲线，可以得到驻波比ρ≤1.99的频带宽度为13.5 MHz，与前面的计算结果12.5 MHz基本一致，这就证明了本文第1节的理论推导是正确的。下面就可利用该方法进行滤波器型输出回路的设计计算了。

4 一个S波段单间隙腔加载滤波器输出回路的自动优化设计

图4 驻波比与频率关系曲线

滤波器型输出回路的设计参数要求：输出波导尺寸为72.14 mm×34.04 mm，在频率2.17 GHz至2.32 GHz的150 MHz的范围内实现间隙阻抗大于等于700 Ω，带内阻抗波动小于1 dB。

根据波导滤波器的设计理论或直接利用1维设计软件FIL5和FILTER即可获得1 dB带宽范围内的阻抗实部最大值Rmax=8 90Ω；输出腔的外观品质因数Qext=90；间隙特性阻抗R/Q=34，以及输出回路上的归一化电纳的电气参数值等，最终通过查表[7]可获得电感钉的个数、位置及直径等几何参数。另外，在利用1维设计软件FIL5和FILTER时，默认设置是1 dB带宽，所以，如果要求的带内阻抗波动不是1 dB(例如3 dB或0.5 dB)，注意更改软件中1维设计软件FIL5和FILTER的参数设置，从而获得相应dB带宽范围内阻抗实部最大值，再完成后续的相应计算。

由前文的论述可知，上述过程确定的几何结构参数往往需要冷测试验调节才能获得准确的值。然而，我们可把上述过程获得的输出回路的各项几何参数值做为初始值，在包含初始值在内的较宽取值范围内，采用本文的“驻波比方法”通过计算机自动优化获得精确的结果。

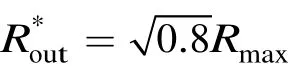
图5给出了单间隙腔加载两节滤波器的输出回路结构示意图，图中标号为1和4的位置放置电容钉，标号为2, 3, 5, 6的位置放置电感钉，L1,L2,L3,L4是电容钉或电感钉与输出腔中心的距离，C1是腔体的直径，C2是漂移头的直径，C3是输出腔间隙距离，H1和H4分别是两个直径为10的电容钉与波导底的距离，B3是标号为2和3的电感直径，B6是标号为5和6的电感直径，D1,D2是两个电感钉之间的距离。表1给出了需要优化的几何参数的初始值。

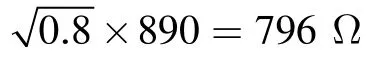
表1 优化参数初始值

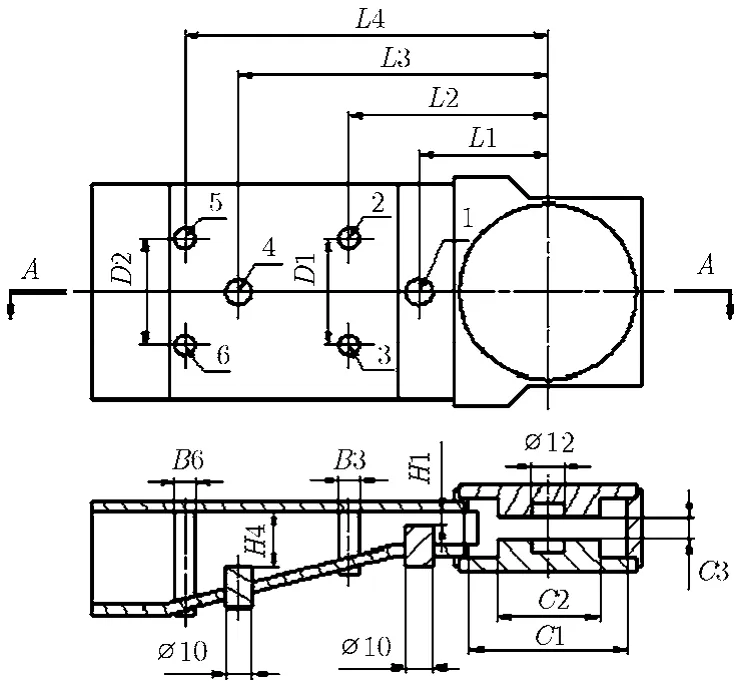
图5 加载滤波器的输出回路的结构示意图

图6给出了计算机完成所有参数组合的计算后自动存储的一条波导端口的驻波比-频率曲线，从图中看出，在频率2.17～2.32 GHz的范围内，波导端口的驻波比ρ≤1.99，表 2是计算机自动存储的一组各项优化参数的数值。由前面的论述可知，满足驻波比ρ≤1.99的曲线不止一种，也即满足要求的参数组合不止一种，此时也可以自己选取其中一种参数组合，通过观察间隙阻抗频率特性来最终确定。

表2 优化得到的电感电容钉的参数值

需要说明的一点：如果既没有滤波器的调试经验，也无法通过1维软件确定滤波器输出回路的电参数以及无法查表获得几何参数的初始值，通过本文的方法仍然可完成滤波器型输出回路的精确设计。具体方法和步骤如下：

(1)根据中心频率及速调管总体设计要求的输出间隙距离，确定输出腔的结构和尺寸。

(2)根据带宽要求确定滤波器的节数，按滤波器的节数设置电感钉，第1个电感钉与耦合孔之间设置第1个电容钉，两个电感钉之间再设置电容钉，按照上述位置关系就可以大概给定电感钉和电容钉的位置参数的初始值。

(3)根据速调管总体设计要求的间隙阻抗，取间隙阻抗的实部作为带宽内的电阻最小值，利用本文前面的理论计算，再根据频带内阻抗波动的要求可得出间隙处应加入的电阻值。

(4)把电感钉的位置、直径、电容钉插入波导的深度及耦合孔的尺寸作为优化参数，再根据带宽范围内阻抗波动的要求确定驻波比ρ的取值范围，并将ρ的取值范围作为优化目标，通过计算机自动优化计算，可获得满足总体设计要求的滤波器输出回路的几何参数组合。

(5)如果电感，电容钉的位置和尺寸及耦合孔的尺寸等参数的初始值不合适，或取值范围过大，可通过多次优化逐渐缩小各项参数的取值范围获得最佳参数组合结果。

总之，利用本文的方法，只需根据速调管总体设计要求的各项指标，将滤波器输出回路中与指标要求有关的各项参数做为优化参数，在输出间隙处加入最佳电阻，设定驻波比ρ的取值范围作为优化目标，完全利用计算机自动优化计算即可获得滤波器型输出回路的优化结果，完成了滤波器的快速设计。

下面对该优化结果的正确性进行验证。

5 优化设计结果的模拟验证和冷测实验验证

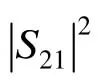
按照上述模拟结果获得的参数值加工冷测模型，并按模拟获得的电感电容的尺寸放置在输出波导上，图8给出了利用“相位法”冷测获得的阻抗频率特性曲线。

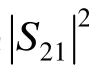
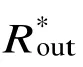
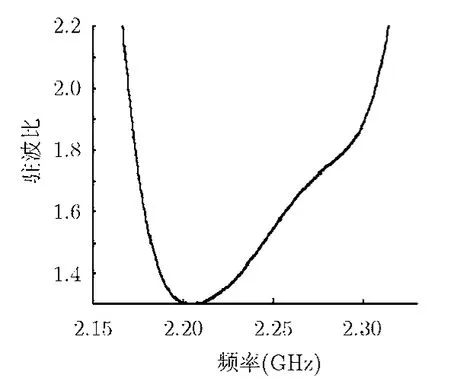
图6 驻波比与频率的关系曲线

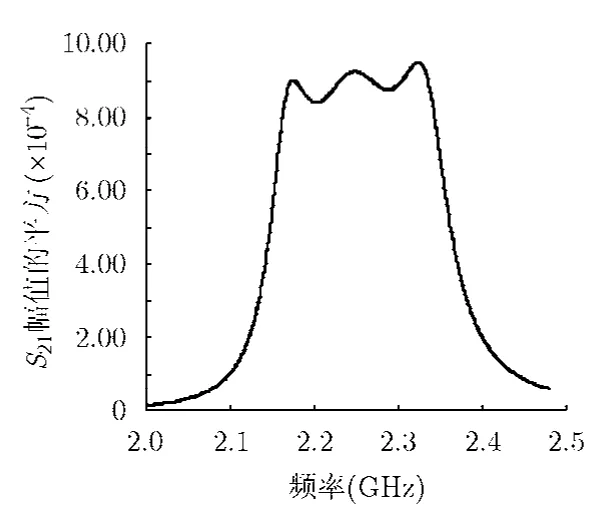
图7 S21幅值的平方频率特性曲线

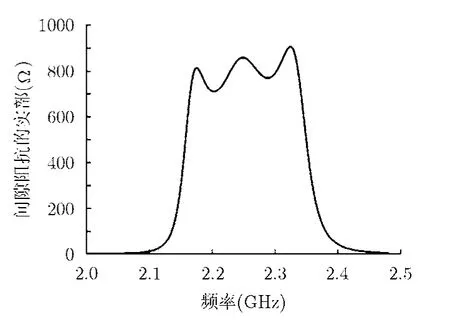
图8 间隙阻抗的实部频率特性曲线

6 结束语

本文以滤波器型输出回路可与波导滤波器进行等效的理论为基础，利用3维微波软件CST可设置“离散端口”的功能，获得了一种通过计算机自动优化设计滤波器输出回路的新方法，减轻了设计人员的模拟或冷测调试滤波器型输出回路的繁杂冗长的工作。同时，在设计滤波器型输出回路时，也可以将本文的提出的新方法与以往文献中的“等效电路法”、“传输法”，“相位法”等方法及冷测试验相结合，快速精确的设计输出回路，进而加快速调管的研制进度。

[1]丁耀根. 大功率速调管的设计制造和应用[M]. 北京: 国防工业出版社, 2011: 200-246.

Ding Y G. Design, Manufacture and Application of High Power Klystron[M]. Beijing: National Defense Industry Press,2011: 200-246.

[2]丁耀根. 大功率速调管的理论与计算模拟[M]. 北京: 国防工业出版社, 2008, 12: 283-358.

Ding Y G. Theory and Computer Simulation of High Power Klystron[M]. Beijing: National Defense Industry Press, 2008:283-358.

[3]电子管设计手册编辑委员会. 大功率速调管设计手册[M]. 北京: 国防工业出版社, 1979: 133-163.

Electronic Tube Design Handbook Editorial Committee,Design Handbook of High Power Klystrons[M]. Beijing:National Defense Industry Press, 1979: 133-163.

[4]林福民, 丁耀根, 张志强, 等. 速调管双间隙腔的间隙阻抗矩阵频率特性的模拟计算方法[J]. 电子与信息学报, 2004, 26(9):1480-1486.

Lin F M, Ding Y G, Zhang Z Q,et al..Simulation computation method for calculation the impedance matrix of double gap cavity of klystron[J].Journal of Electionics&Information Technology, 2004, 26(9): 1480-1486.

[5]王进华, 丁耀根. 场分析法与阻抗叠加方法在速调管输出腔间隙阻抗计算中的应用[J]. 强激光与粒子束, 2006, 18(2):245-248.

Wang J H and Ding Y G. Application of field analysis method and impedance superposition method in gap-impedance calculation of klystron output circuit[J].High Power Laser&Particle Beams, 2006, 18(2): 245-248.

[6]曹静, 丁耀根, 沈斌, 等. 传输法模拟滤波器型输出回路的间隙阻抗频率特性[J]. 真空科学与技术学报, 2012, 32(5):399-403.

Cao J, Ding Y G, Shen B,et al..gap-impedance simulation of output circuit with filter in transmission method[J].Chinese Journal of Vacuum Science and Technology, 2012, 32(5):399-403.

[7]Marcuvitz N. Waveguide Handbook[M]. McGraw-Hill Book Company, Inc, 1951.

[8]张丁, 曹静, 缪亦珍, 等. 群时延时间求解速调管输出腔的外观品质因数Qext[J]. 真空科学与技术学报, 2007, 27(5):391-394.

Zhang D, Cao J, Niu Y Z,et al..Calculation of external-quality factor out-put cavity of klystron with group delay time method[J].Chinese Journal of Vacuum Science and Technology, 2007, 27(5): 391-394.

[9]张敏. CST微波工作室——基础入门[M]. 北京: 电子工业出版社, 2006: 81-83.

Zhang M. CST Microwave Studio— Basics[M]. Beijing:Publishing House of Electronics Industry, 2006: 81-83.