多目标约束下的光突发交换网络组装参数分析

牛大伟 于卫波 米志超 王 海 董 超 赵文栋

(解放军理工大学通信工程学院 南京 210007)

1 引言

光突发交换(Optical Burst Switching, OBS)是一种在光层直接进行报文级交换的技术，具备密集波分复用系统中波长资源的统计复用能力。在向全光交换演进的过程中，OBS网络被认为是一种较为中肯的、可实现性较强的方案[1]。OBS中的入口边缘节点对接入网络的数据进行排队组装，并在一定触发条件下将队列中的数据集中组装成一个突发，进行突发发送。网络中的核心节点对接收到的突发在光域进行无光电转换的透明转发并在出口边缘节点进行光电转换、解组装和报文分发等操作。为实现核心节点的光域透明转发，入口边缘节点一般在发送数据突发之前利用专用控制波长提前发送控制报文。控制报文在核心节点进行光电转换，并执行选路、资源预留和交换矩阵配置等操作。如果核心节点的控制平面成功预留了输出链路的资源，则延迟到达的数据突发可在光域实现透明转发，反之将被核心节点丢弃。

OBS网络边缘节点的组装算法是影响网络性能的一个重要因素。目前提出的组装算法主要分为两类即固定门限组装算法[2,3]和动态门限组装算法[4,5]。固定门限算法不适合在未来光交换网络中实用。动态门限算法可以依据接入网输入速率或者核心网络负载状态的变化动态调整组装触发门限值，以达到自适应网络状态的变化。文献[5]提出的动态组装算法以边缘节点统计的接入网络速率为输入参数，当接入流量较大时使用较大的门限以平滑输出突发流量(以Bursts/s衡量)，反之则使用较小的门限以降低组装时延代价。这一类算法仅考虑组装算法对接入流量的整形作用而未考虑网络背景流量和核心节点处理能力对组装算法的约束。文献[4]提出的动态算法以核心节点控制平面所能承受流量上限为约束，根据核心节点网络流量的状态动态地调整边缘节点的组装门限以适应核心节点承受能力。上述动态算法仅从对接入流量整形和限制突发输出速率以适应核心节点控制平面处理能力的角度对组装门限进行优化。事实上，边缘节点组装算法参数对OBS网络中的多种性能都有较大的影响。例如：组装算法输出的平均突发长度决定了 OBS网络数据平面的碰撞概率；平均突发持续时间与光交换矩阵配置时间的比值决定了平均链路资源利用率；组装算法的突发输出速率决定了核心节点控制平面的排队时延。另外，不同的网络配置对边缘节点组装算法门限的动态调整需求也不尽相同。例如：具备波长转换能力的核心节点相对于无波长转换能力的节点对组装算法的输出速率更为敏感[6]。组装算法与上述网络性能和网络配置参数的相关性对动态算法提出了更高的要求，即动态算法应该能够在满足上述不同网络性能的约束下，根据不同的网络配置情况动态地决定组装门限的取值范围。本文研究了如何在多种网络性能目标约束条件下确定组装算法有效的队列门限和时间门限。文章第2节分析了边缘节点组装算法门限值与多种网络性能之间的约束关系；第3节分析了波长转换器的配置对有效组装门限的值的影响；第4节通过数值仿真讨论了多种网络性能目标约束条件下的有效组装参数选取问题，为OBS网络配置和参数选取提供依据；第5节是结束语。

2 组装算法门限与网络性能约束

OBS网络中的边缘节点组装算法的参数是指触发突发发送的时间门限Tth和队列门限Lth，如图 1所示。图中O点为组装队列创建起始点(即首个接入报文的到达时刻)，横轴为从起始点计时的时间坐标轴，纵轴为队列长度。图中的斜线OB和OC分别表示在不同接入速率(bit/s)下，组装队列状态的变化轨迹，用斜率λ1和λ2表示。当接入速率λ不断增大时，固定门限的组装算法会导致核心节点控制平面的负载增大并引起较大的排队时延和早到丢弃率[7]。一些动态组装算法[4]虽然部分解决了组装门限动态匹配接入速率的问题，但是没有分析组装门限的调整与网络性能指标之间的相互影响。事实上，在一定的节点处理能力、网络参数以及网络流量的条件下，组装算法的组装门限存在一个有效取值区间。如图2所示，[Tmax,Tmin]为组装算法时间门限的有效区间，[Lmax,Lmin]为组装算法队列门限的有效区间。动态组装算法依据网络状态调整的组装门限值不应该超出图中门限的有效区域(即阴影所示范围)，否则将无法满足OBS网络的目标性能约束。本节将重点讨论如何确定组装算法门限的上下界，从而满足控制平面和数据平面的性能需求。

2.1 组装算法的时间门限取值

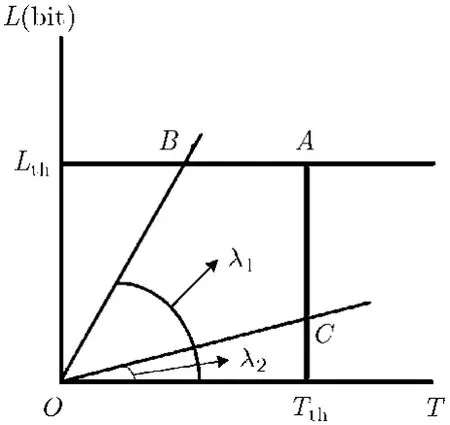
图1 固定门限组装算法

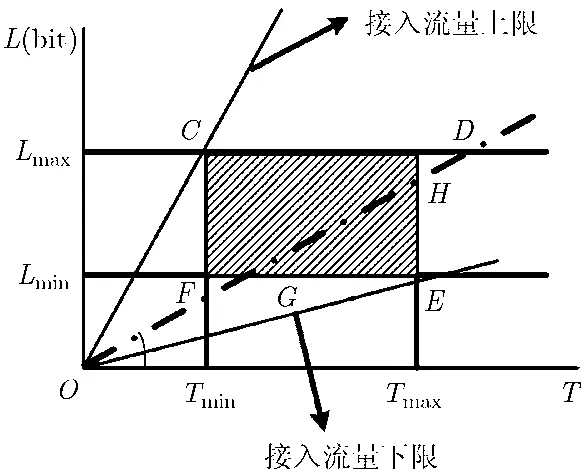
图2 动态门限组装算法

OBS网络边缘节点的组装时间门限直接决定了边缘节点输出突发的速率并引入了组装时延。假设边缘节点组装算法的平均组装时间为Tth，则该节点输出的突发速率为λB=1/Tth。假设网络中流经每个核心节点的平均数据流数为K(以数据的入口边缘节点和出口边缘节点地址对标识流)，则通过核心节点的平均背景流量为λc=λB1+…+λBK，其单位为突发/s(Bursts/s)。由于OBS网络中控制平面对资源的正确预留是成功转发数据突发的前提，所以必须保证输入核心节点的总背景流量λc低于核心节点控制平面的处理速率上限。假设核心节点处理 1个突发控制报文的时间为1 μs，通过核心节点的K个数据流具有相互独立同分布的输入流量且要求核心节点输入的背景流量归一化负载上限为κ(0＜κ＜ 1)。则每个边缘节点的突发输出速率上限应为λB=1/Tth≤κ·μ/K，则每个边缘节点的组装算法时间门限下限如式(1)所示。

式(1)表明，组装算法时间门限下限的取值受核心节点控制平面处理能力约束。当组装算法的时间门限值低于式(1)中的Tth时，输入核心节点控制平面的总背景流量将超过其归一化负载上限κ，从而导致突发控制报文队列的溢出和丢弃。

另外由于核心节点控制平面对突发的处理采用存储转发模式，则突发控制报文在核心节点控制平面的逗留时间可利用M/G/1或M/D/1模型计算得出[6]。假设突发逗留平均时间为W(λc)(其中λc为核心节点控制平面的背景流量)，则边缘节点组装算法输出突发的平均间隔应该大于W(λc)，即Tth≥W(λc)，否则核心节点的队列长度将趋于无穷大。综合式(1)可得出最小组装时间门限的取值标准如式(2)。式(2)的工程含义为：边缘节点组装算法的时间门限的下限受核心节点控制平面处理能力及其背景流量约束，其中的背景流量可以采用OBS网络测量的方法实时获取[7]。

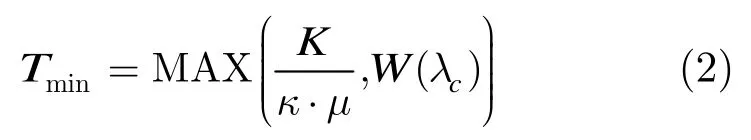
组装算法时间门限的上限Tmax主要受端到端可接受时延的限制，例如对于一般的IP业务而言，干线网络的可接受时延约为10 ms左右。因此，一般Tmax选择固定值Tmax=TE，其中TE为数据业务端到端可接受时延的上限。

2.2 组装算法的队列门限取值

OBS网络边缘节点的队列门限决定了边缘节点输出数据突发的长度。假设边缘节点组装算法的队列门限为Lth且传输链路速率为Cbit/s，则边缘节点输出的数据突发的持续时间为TB=Lth/C。在OBS网络中，控制平面成功预留波长资源后将在数据突发到达时刻前完成光交换矩阵(也可称为光交叉连接器 OXC)的配置，使输入链路的波长信道与输出链路的波长信道实现联通。OXC断开原有连接并建立新的连接需要一定的时间，在这段时间内链路无法传输数据，这个时间称之为OXC配置时间Toxc。目前的：OXC主要为基于MEMS器件和基于声光器件两类[8,9]，其配置时间从10 μs到10 ms不等。由于存在OXC配置时间，则输出链路信道的相邻占用状态之间的空闲状态的持续时间应至少大于OXC配置时间，否则信道的占用状态为无效占用，即无法完成控制平面预期的数据转发功能。假设网络中目标信道负载率下限为η(0＜η＜1)，则(TB/(TB+Toxc))≥η，假设信道速率为C，则可得到边缘节点组装算法队列门限的取值下限Lmin如式(3)所示。

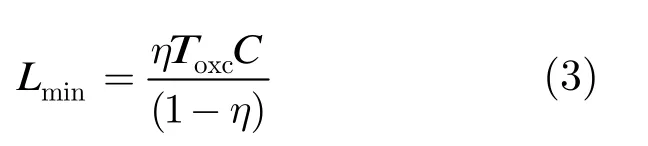
式(3)的工程含义为：边缘节点组装算法的队列门限的下限受核心节点光交换矩阵配置器件的约束。在一定的期望波长资源利用率约束条件下，OXC设备配置时间越长，则组装算法的最小队列门限值越大，反之则最小队列门限值越小。

OBS网络的数据平面是无缓存的全光交换，当输出链路存在争用时(资源竞争)，无缓存系统将产生突发丢失现象。因此，网络规划必须设定一个最低期望突发丢失率Pb以满足用户业务的服务质量需求。假设输出波长资源的数目w为服务员的个数，输入数据突发的背景流量为λc(Bursts/s)且满足泊松分布，由上述分析可知，数据突发的平均持续时长TB=Lth/C即为服务员的平均服务时间。由排队理论分析，此时的突发丢失率可由爱尔兰B公式[10]计算。为满足期望的丢失率Pb的需求，则组装算法的队列组装门限的上限Lmax如式(4)所示。其中的Erlb(·)为一定的突发丢失率、背景流量以及波长数目的约束条件下调用爱尔兰B公式计算的最大突发持续时间。式(4)的工程意义在于，边缘节点组装算法队列门限的上限受 OBS网络数据平面突发丢失率性能和背景流量状态的约束，期望丢失率越低，背景流量越大则队列门限取值的上限约束值越小即有效取值区域越小，反之上限约束值越大即有效取值区域越大。

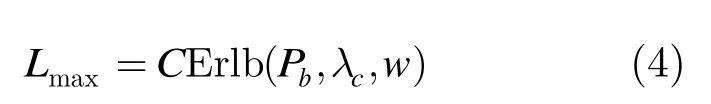
综上所述，OBS网络边缘节点动态组装算法的触发门限的有效取值区域受网络控制平面处理能力、数据平面的期望丢弃概率、链路资源的利用效率以及网络核心节点背景流量等多种网络性能和网络状态的约束。动态算法必须根据网络状态和约束目标的变化实时调整门限参数上限和下限并且在有效区域内动态调整门限值。本节的组装门限区域可归纳为式(5)。

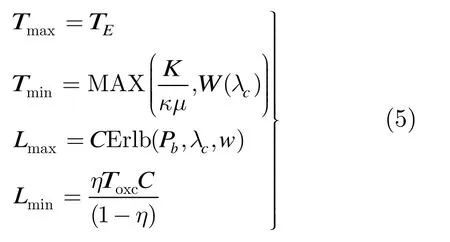
3 波长转换器对组装算法的门限取值的影响

分析式(5)可知时间门限的下限Tmin所涉及的突发控制报文排队时延W(λc)与核心节点控制平面的处理能力密切相关。根据文献[6,11]，核心节点波长转换器的配置对控制平面的处理能力会产生较大影响，配置波长转换器的核心节点将执行更复杂的查表和资源预留操作，在相同背景流量条件下会带来更大的排队时延。另外，在数据平面出现资源冲突时，未配置波长转换器的节点无法利用转换波长来避免突发的碰撞和丢失，所以其碰撞概率较大且直接影响式(5)中的Lmax。本节重点讨论核心节点波长转换器的配置对组装算法门限的影响，并分两种情况重新计算式(5)。

3.1 核心节点无波长转换器

当核心节点未配置波长转换器时，其控制平面对突发仅做一次比较运算，即判断该突发是否能在入口节点指定的波长上转发。这个操作较为简单，硬件实现的运算时间几乎为确定的。此时可将核心节点建模为M/D/1排队系统。假设核心节点队列的背景流量为λc(Bursts/s)；节点的处理时间为τs(此处的τ为资源预留算法的一次比较时间)；突发控制报文在队列中的逗留时间的概率密度函数为w(t)，则由文献[6]可知，突发控制报文在核心节点的平均逗留时间概率密度函数w(t)如式(6)所示，其中的系数a(λ)由式(7)给出，μ=1/τ为控制平面的平均处理速率。

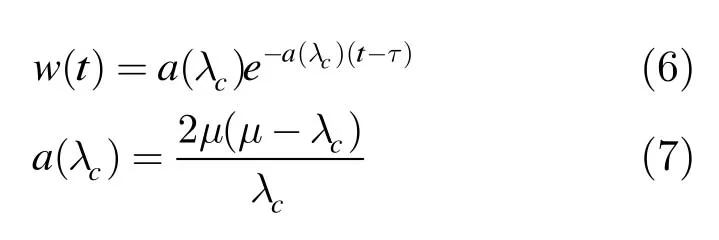
对式(6)中的t求均值可得到无波长转换器条件下，突发控制报文在核心节点平均逗留时间如式(8)所示。

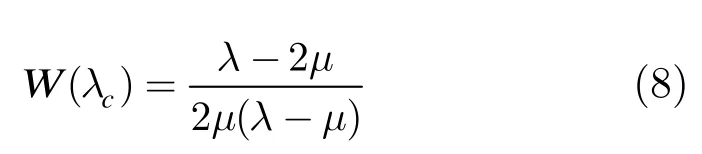
当数据突发穿越无波长转换器的核心节点时，仅能由输出链路的确定波长进行转发而无法在资源冲突时选择其他空闲波长传输即仅存在唯一服务员(式(4)中w=1)，此时式(4)可以写为Lmax=CE rlb(P0,λc,1)。则在核心节点未配置波长转换器时，边缘节点组装算法门限的有效取值范围如式(9)所示。

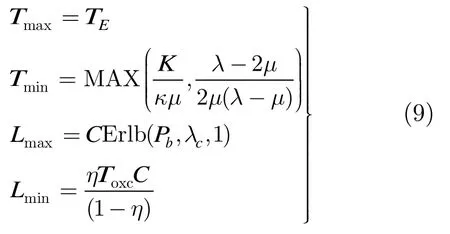
3.2 配置波长转换器的核心节点模型

当核心节点配置了波长转换器时，资源预留算法需要在多个可用波长信道中选择一个最优转发信道。此时突发控制报文在控制平面的逗留时间取决于资源预留算法的时间复杂度，不同的资源预留算法，其处理时间的概率分布不同。核心节点控制平面对突发控制报文的处理时间的分布概率如式(10)所示[11]。其前提条件为偏置时间为区间[0,D]内均匀分布的随机变量，其均值为D/2。

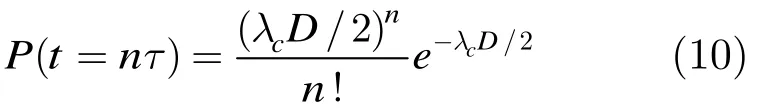
在输入背景流量为泊松分布时，可以使用M/G/1模型分析控制平面的排队行为。则突发控制报文在核心节点的平均逗留时间如式(11)所示[6]。其中N=D/τ即最大偏置时间相对于控制平面一次查表比对时间的倍数。

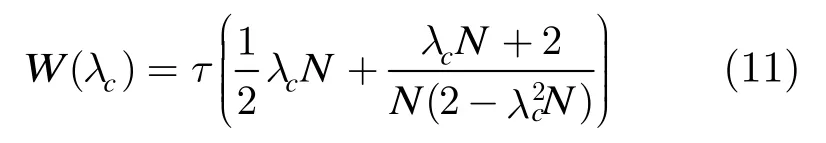
分析式(11)可以看到，当公式右侧第 2项分母趋向于 0时平均逗留时间W(λc)为无穷大，此即控制平面所能承受的背景流量极值，如式(12)所示。

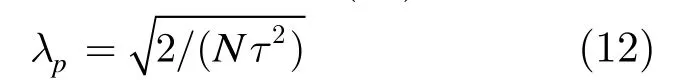
可以认为当输入背景流量如式(12)所示时，控制平面的归一化负载达到 1。若核心节点允许输入的目标归一化负载为κ，则将式(11)和式(12)代入式(2)可得到组装算法时间门限下界如式(13)所示。

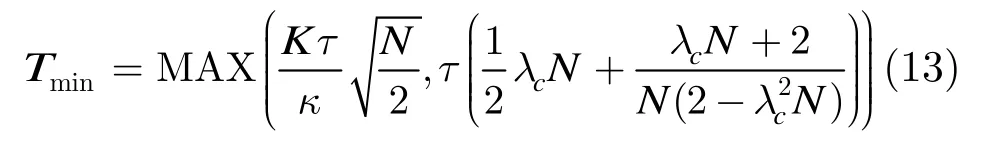
假设核心节点配置了w个波长转换器，则存在w个服务员为输入链路到达的数据突服务，此时的数据平面可采用M/M/w/w排队模型建模。将式(13)代入式(5)且当 OBS网络中的核心节点配置的波长转换器数目为w时，其边缘节点组装算法的组装门限取值区域如式(14)所示。

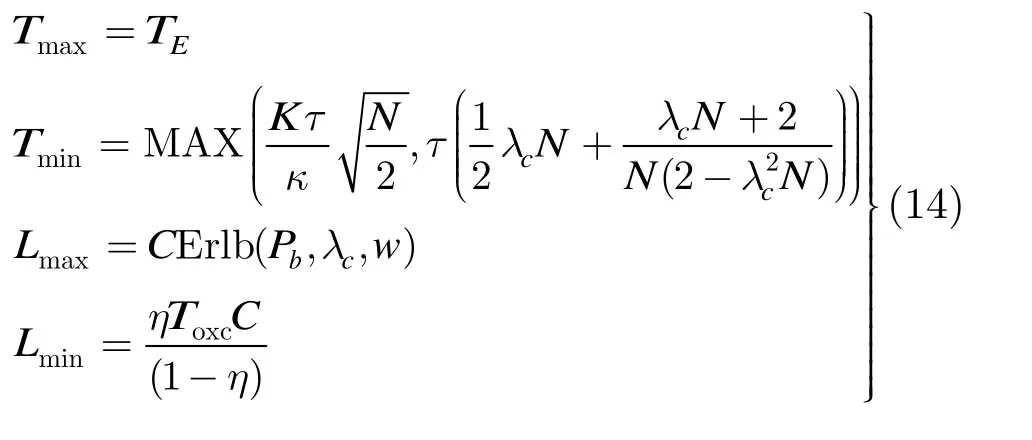
4 仿真分析

本节利用数值仿真定量分析了不同目标约束条件和节点配置条件下网络边缘节点组装算法的组装门限取值范围以及可行的组装参数对网络配置的需求。

4.1 无波长转换器条件下的仿真分析

图3为无波长转换器条件下组装算法门限取值范围的数值仿真分析。图中的曲线为最大突发持续时间(依据组装算法队列门限的上限Lmax换算，二者物理含义一致)与核心节点背景流量关系图。横轴为核心节点控制平面的背景流量(单位为 Bursts/s)，纵轴为最大突发持续时间(单位为s)。约束条件为：η=90%;Toxc=1 ns, 100 ns, 1 ms ;Pb分别为 10-1到 10-5。Bmax和Bmin分别代表由最大队列门限和最小队列门限计算获取的最大和最小突发持续时间。可以看到，若要求存在有效的队列门限(即Bmax＞Bmin)，则必须选用配置时间极快(小于1 ns)的OXC设备，否则就要降低网络性能的目标需求。而目前的较成熟的光开关技术的配置时间一般在 1 ms以上[8]。所以在现有的光开关技术条件下，核心节点无波长转换器时，几乎无法满足网络的性能需求。其原因在于数据平面的服务员数仅为 1，碰撞概率较大。

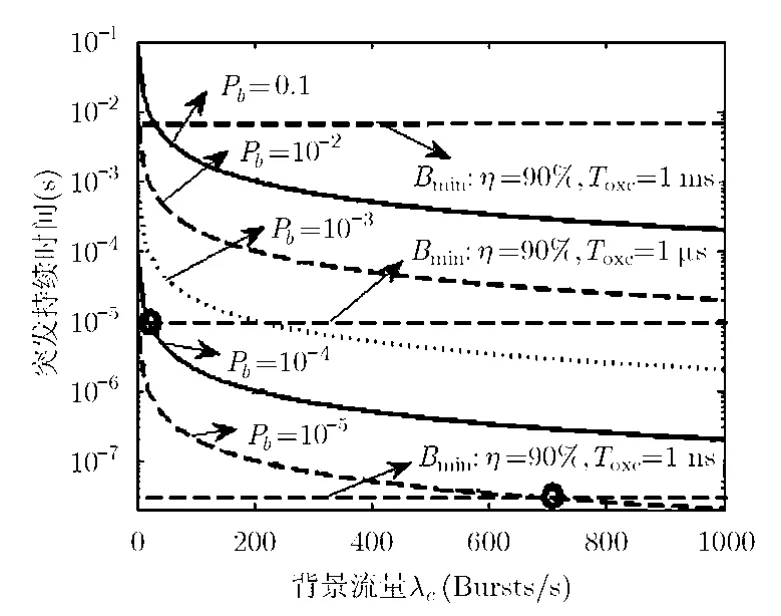
图3 无波长转换器的突发持续时间约束

4.2 配置波长转换器条件下的仿真分析

图4为配置波长转换器条件下，数据平面约束下的最小和最大突发持续时间的示意图。其横轴和纵轴与图3相同，Pb为 10-5。可见，要保证存在有效突发持续区间(即Bmin＜Bmax)，则至少需配置30个波长转换器。同时比较图4和图3可以看到，在核心节点配置波长转换器后，对OXC配置时间的约束也大大放宽，如图中所示，在Toxc=1 ms时，只要波长转换器的数目大于30，则均可找到有效的队列门限。

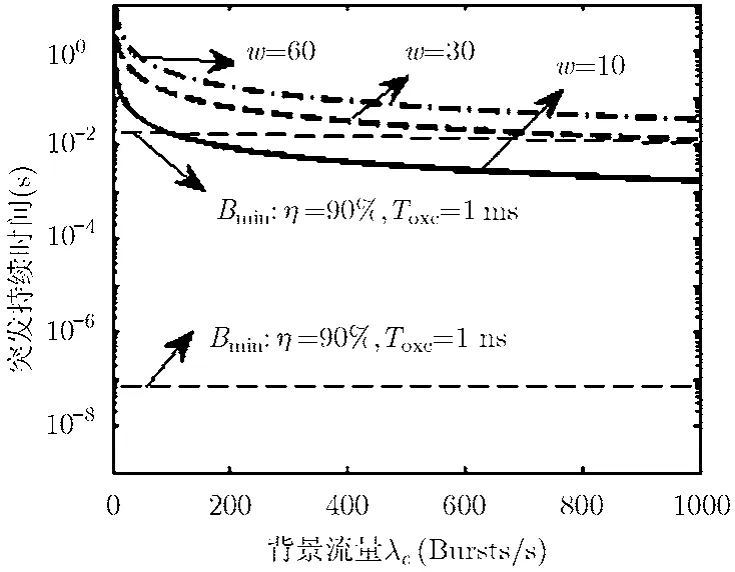
图4 配置波长转换器的突发持续时间约束

图5为突发持续时间与网络参数之间的约束关系曲线图。图中曲线是在归一化背景流量为λc=0.9，偏置时间N=100条件下的数值曲线。图5(a)给出了最小突发持续时间与 OXC设备配置时间的关系曲线。可以看到，当OXC配置时间为1 ms时，突发持续时间下限为Bmin=10 ms 左右(η=90%)。此时若要求队列门限有效取值区间存在，要求突发持续时间上限Bmax＞10 ms。由图 5(b)可知，满足条件的前提为w＞20(目标突发丢弃率Pb=0.1)，一般而言，若要为用户保证一定的服务质量，则目标突发丢弃率应小于 10-4，则此时所需要波长转换器数目至少大于30，这一因素也决定了在现有光器件的条件下，建设工程上可行的OBS网络，需要较大的成本。

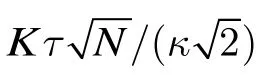
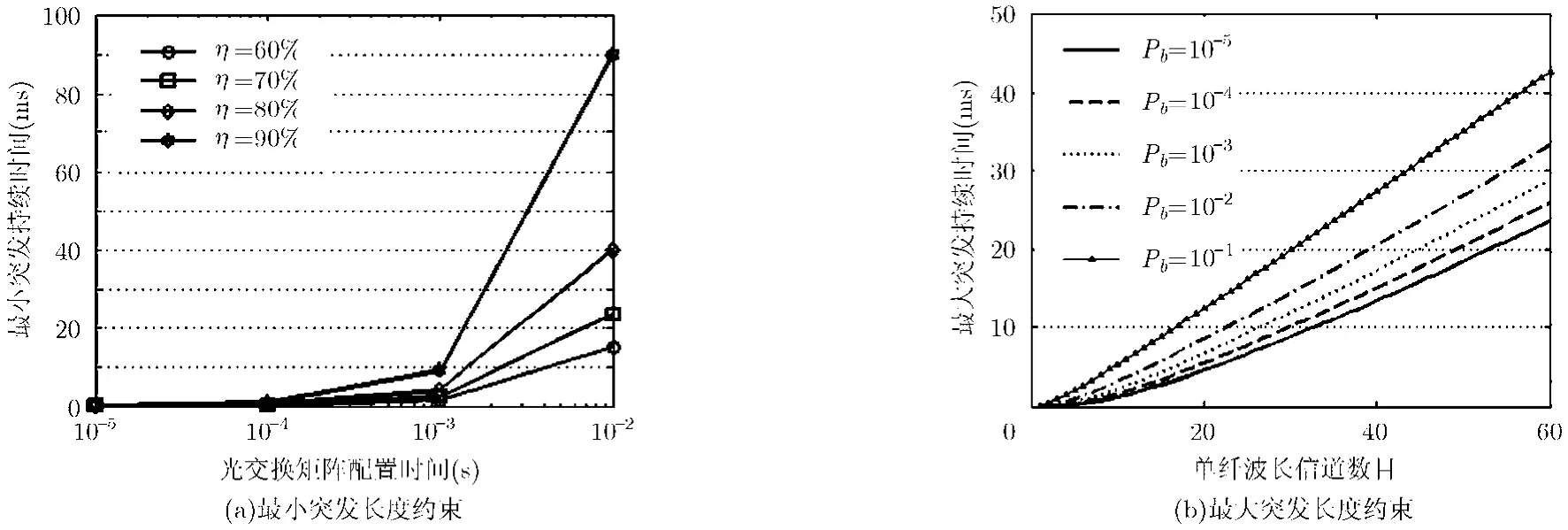
图5 突发持续时间与节点参数的关系

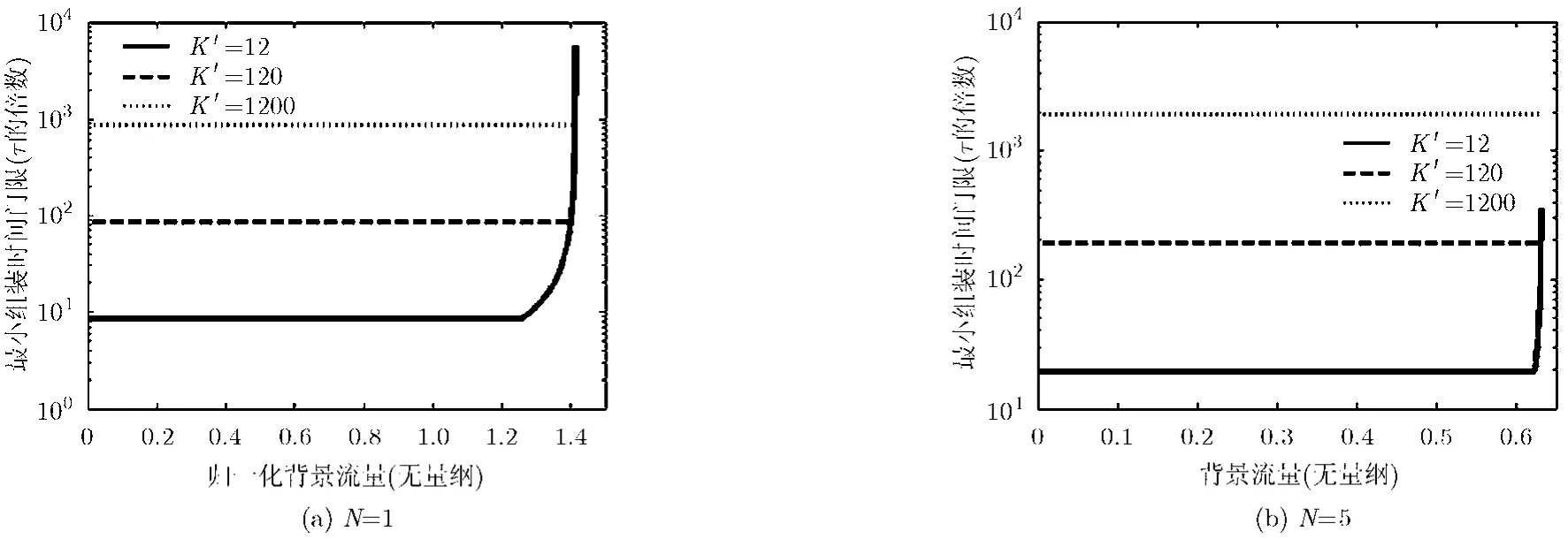
图6 配置波长转换器条件下的最小时间组装门限

5 结论

本文研究了在多种网络性能指标约束下的OBS网络边缘节点组装算法门限值的取值区间问题。通过分析认为，利用无波长转换器核心节点构建的OBS网络几乎无法找到有效的队列门限值，因此无法达到可行的网络性能指标。在现有光器件的条件和较合理的网络期望性能约束下，核心节点至少需要配置约30个波长转换器，否则将无法满足数据平面的性能需求。

[1]管爱红, 王波云, 张元, 等. 光突发交换网络中基于优先级与突发包分割的光缓存方法[J]. 激光与光电子学进展, 2011,48(6): 060601-1-060601-6.

Guan Ai-hong, Wang Bo-yun, Zhang Yuan,et al.. Optical buffer mechanism based on priority and burst segmentation in optical burst switching networks[J].Laser&Optoelectronics Progress, 2011, 48(6): 060601-1-060601-6.

[2]Ge A, Callegati F, and Tamil L. On optical burst switching and self-similar traffic[J].IEEE Communicatoin Letters, 2000,4(3): 98-100.

[3]Vokkarane V M, Haridoss K, Jue J P. Threshold-based burst assembly policies for QoS support in optical burst-switched networks[C]. SPIE Optical Communication, Boston Mass USA, 2002: 125-136.

[4]Toksoz M A and Akar N. Dynamic threshold-based assembly algorithms for optical burst switching networks subject to burst rate constraints[J].Photonic Network Communication,2010, 20(2): 120-130.

[5]C Yuan, Zhang R Z, Li Z B,et al.. A unified study of burst assembly in optical burst switching networks[J].Photonic Network Communication, 2011, 21(3): 228-237.

[6]牛大伟, 王海, 于卫波, 等. 一种适用于光突发交换网络的背景流量估计模型[J]. 光学学报, 2012, 32(11): 1106002-1-1106002-5.

Niu Da-wei, Wang Hai, Yu Wei-bo,et al.. A cross traffic estimate model for optical burst switching networks[J].Acta Optical Sinica, 2012, 32(11): 1106002-1-1106002-5.

[7]牛大伟, 彭来献, 于卫波, 等. 一种基于控制平面测量的光突发交换网络动态偏置时间算法[J]. 电子与信息学报, 2012,34(4): 776-781.

Niu Da-wei, Peng Lai-xian, Yu Wei-bo,et al.. Control plane measurement based dynamic offset time algorithm in optical burst switching networks[J].Journal of Electronics&Information Technology,2012, 34(4): 776-781.

[8]乐孜纯, 陈君, 付明磊, 等. 一种新型结构光交叉连接节点及其联网性能分析[J]. 光学学报, 2011, 31(3): 0306005-1-0306005-7.

Le Zi-chun, Chen Jun, Fu Ming-lei,et al.. Optical cross connection: novel architecture and performance analysis[J].Acta Optical Sinica, 2011, 31(3): 0306005-1-0306005-7.

[9]胡卫生, 孙卫强, 何浩, 等. 光交换的时间及空间结构分析[J].激光与光电子学进展, 2012, 49(1): 010001-1-010001-6.

Hu Wei-sheng, Sun Wei-qiang, He Hao,et al.. Time structure and space architecture of optical switching[J].Laser&Optoelectronics Progress, 2012, 49(1): 010001-1-010001-6.

[10]Kleinrock L and Gail R. Queuing Systems: Problems and Solutions[M]. New York: Wiley-Interscience Publicatoin,1996, 119-179.

[11]Pedro L de, Aracil J, Hernandez J A,et al.. Analysis of the processing and sojourn times of burst control packets in optical burst switches[C]. Proceedings of International Conference on Optical Networks Design and Modeling,Catalonia Spain, 2008: 1-3.