贝特朗悖论与随机模拟方法

☉湖北省鄂州市吴都中学 吴 超

☉鄂州市新民街小学 阮宏兰

在中学概率统计部分的学习中，几何概型问题看似简单，却又不好把握.解决几何概型问题的关键在于问题的转化：准确地构造出可度量的有限几何区域（样本空间）.特别要注意的是无限性、等可能性、有限性在解决问题中的体现.在本文中我们用随机模拟方法来讨论几何概型问题.

随机模拟方法是利用计算机或者计算器模拟试验从而计算事件发生概率的一种方法.在模拟试验过程中我们会重复产生随机数模拟事件是否发生.利用事件发生的频率作为事件发生概率的近似估计.这里的随机数是在一定范围内产生的数，并且得到这个范围中的任一个数的机会是均等的.因此对几何概型中事件发生的概率计算可以用随机模拟方法实现.下面我们用历史上著名的贝特朗悖论来说明这个问题.

1899年，法国学者贝特朗提出了所谓“贝特朗悖论”：从一圆内所有的弦中任意取一条弦，求该弦的长度大于圆内接正三角形边长的概率.

一、问题分析

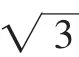
二、问题转化

考虑用计算机或者计算器模拟这个试验：从单位圆中任意取一条弦，则如何确定弦的位置？

情形1 弦由它在圆周上的两个端点确定

此时认为弦的两个端点可以分别在单位圆周上等可能地选取.而单位圆周的周长为2π，在圆周上任取一点为0点，沿顺时针方向定义任一点的位置为该点到0点的距离.不妨设两个端点在单位圆周上的位置为x和y，如图1，则事件A等价于：

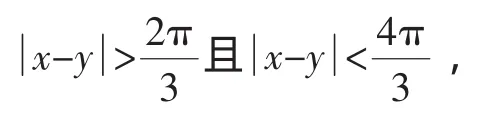
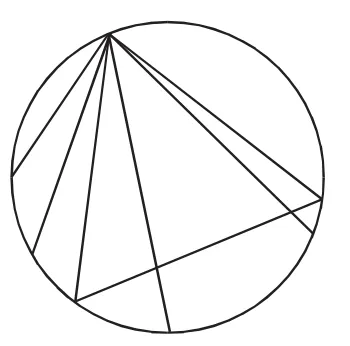
图1

图2

计算器或计算机模拟步骤如下：

（1）产生两组0～1区间的均匀随机数（共有N对）：x1=RAND，y1=RAND；

（2）经伸缩变换：x=x1×2π,y=y1×2π；

试验次数为10000时模拟事件发生的概率近似值为0.3373.

情形2 弦由它的中点确定

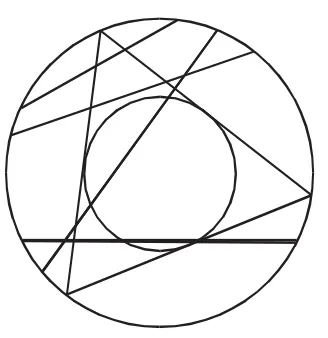
图3

计算器或计算机模拟步骤如下：

（1）产生两组0～1区间的均匀随机数，x1=RAND，y1=RAND；

（2） 经平移和伸缩变换得到，x=（x1-0.5）×2，y=（y1-0.5）×2；

试验次数为10000时模拟事件发生的概率近似值为0.2563.

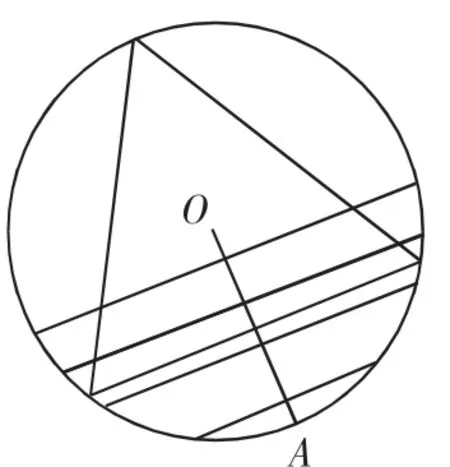
图4

计算器或计算机模拟步骤如下：

（1）产生一组0～1区间的均匀随机数（共有N个），x=RAND；

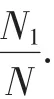
试验次数为10000时模拟事件发生的概率近似值为0.4984.

结果分析：

同一问题由于对等可能性的不同解读导致有三种不同答案，相应的样本空间也不相同.具体如下：情形1中假定弦的两个端点在圆周上等可能地选取，圆周上任意选取的两个点组成样本空间Ω1；情形2.1中假定弦的中点在大圆内等可能地选取，大圆内任意选取的点组成样本空间Ω2；情形2.2中假定弦的中点在半径上均匀分布，半径上任意选取的点组成样本空间Ω3.

由此可以看出：在解决几何概型问题时如何选取合适的样本空间将导致问题的结果迥然不同.不过由于贝特朗悖论本身是一个病态问题，因此这三种答案都不能认为是错误的.其中最接近物理学原理的答案应是情形2.1中的答案.