探求解题思路的几种有效策略

☉江苏省大丰高级中学 姜兴荣

解题者探求解题思路的过程，实质上就是解题者依托自己的知识结构、思想方法、解题经验和思维能力，通过对题目条件、结论及它们之间的关系进行积极主动的思维分析，受其中某些信息的启示和诱发，萌生解题念头、探索解题方法的过程.如何进行“积极主动的思维分析”是探求解题思路的关键所在，对此，本文结合一些实例谈谈几种有效的思维策略，以期抛砖引玉.

一、通法起步、多角度思考

从题目涉及的数学知识出发，直接运用相关数学概念、公式、定理进行解题，是寻求解题思路的首选策略，但未必是最佳解法.多角度地探求问题的解法，往往能获得很多优美、简捷的解法，更重要的是锻炼了思维，发展了能力.

解析一：“分离变量法”是处理不等式恒成立问题的优先之策.

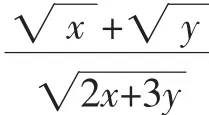
解析二：不等式两边平方是化去根号的常用之法.

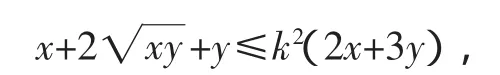
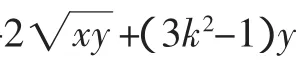
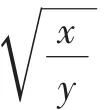
解析三：由根号想到向量的模是一个新的思考角度.

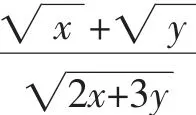
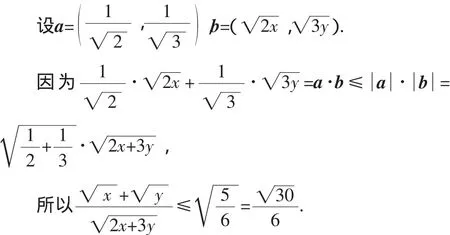
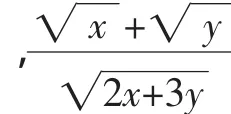
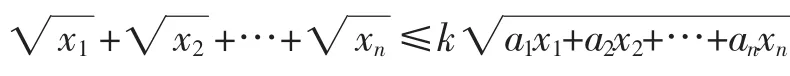
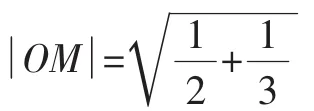
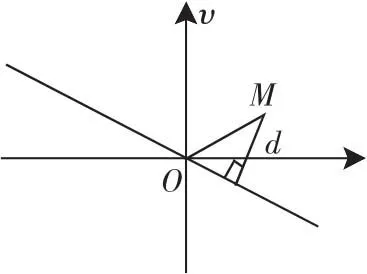
图1

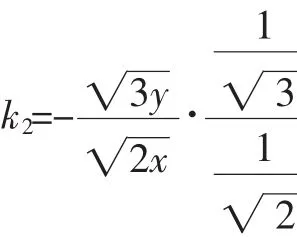
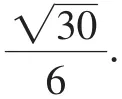
二、观察特征，巧思善构

解题者在长期的数学学习和解题实践过程中，由于经验的作用、思维的积淀，会在自己的认知结构中形成一定思维模块，如具有特定意义的某些符号表达式及相应的处理范式、某些基于基础知识的引伸性结论及常见运用技巧等.解题时，解题者要善于捕捉蕴含于题意中的某种思维模块特征，展开联想，巧妙构造.

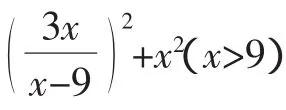
解析一：经观察易知：该函数表达式呈平方和的特征，联想到距离的知识，可尝试构造图形求解.

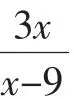
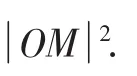
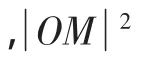
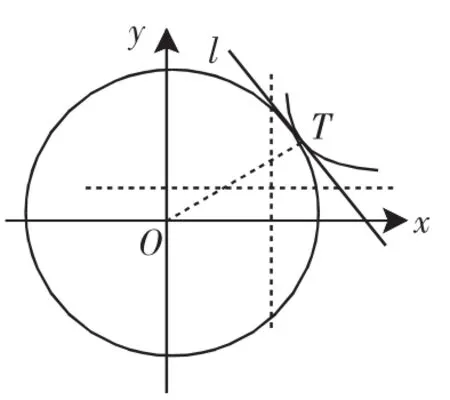
图2

过点T作圆与双曲线的公切线l，设T（x0，y0），

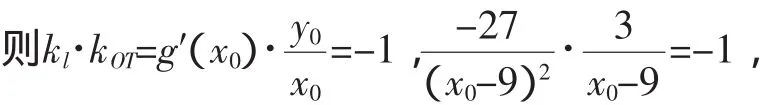
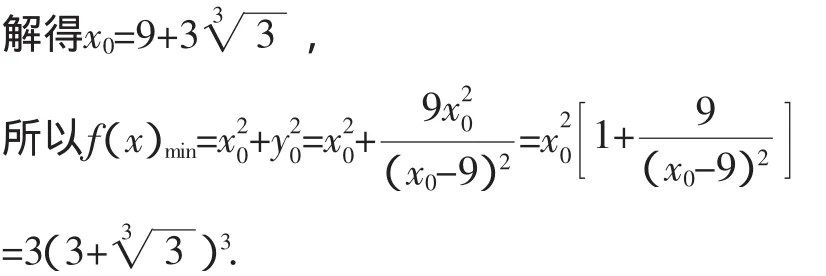
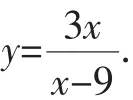
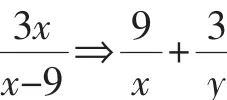
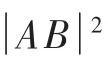
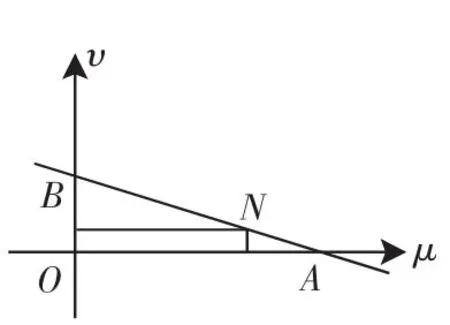
图3

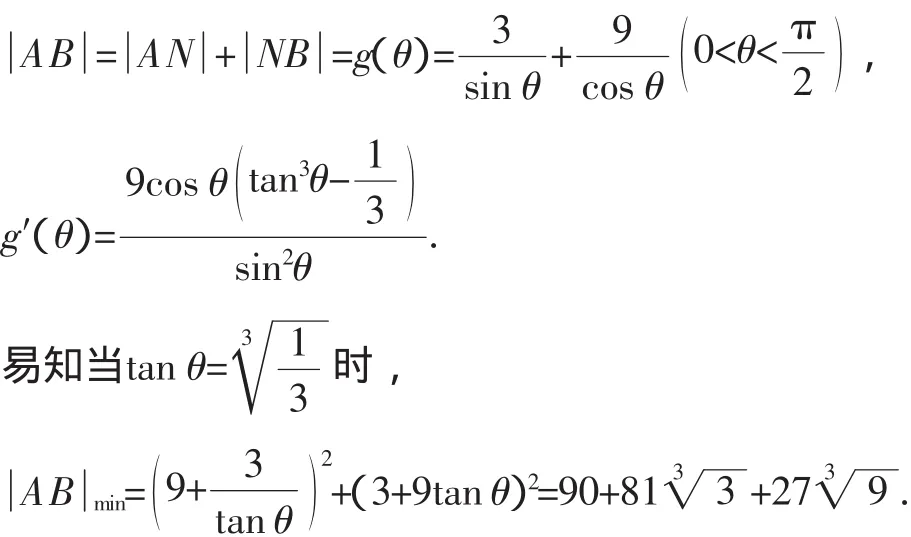
注：本题也可用导数法直接求解.

三、渐趋缩小，逼近目标

含有多元变量、字母参数的问题是一类比较复杂的数学题型，常常要讨论其中一个或几个变量或参数的取值情况，如满足条件的某个或某些字母的取值存在性问题，某个变量的取值范围问题等.

抓住题意中变量、字母间的相互制约关系，利用其中一些变量的取值要求，缩小其他变量或字母的取值范围，使得问题的讨论渐渐趋近求解目标.

解析一：由题意知：字母m，n满足等量关系，利用n的正整数取值要求，来研究m的取值范围，进而，从所推范围中易知m的取整情况.

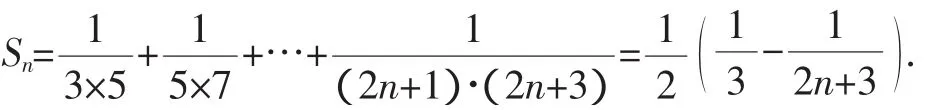
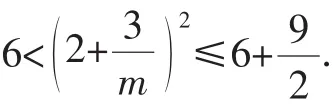
所以m的可能取值为2，3，4，5，6.

当m=3时，代入②式，解得n=3.

当m≥4时，n被m整除，设n=km（k∈N*），代入②化简得：

同理，k=sm（s∈N*），代入③式得：2sm2+9=3s（3+4m），

所以s可能取值为1，3，9，代回④式检验易得：m=6，再代入②式得n=36.

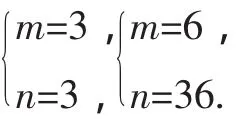
注：解析二的策略是：将两个量m，n之间的整除性关系，逐步缩小为较小的整数9是正整数s的倍数关系而获解的.

四、重新表征、模式转换

数学题是用文字、符号、图形三种语言成分呈现的，揭示了一定的数学本质、数学规律，是相应数学内容的语言表征形式.同一个数学问题可以有不同的语言表征形式，故对所给数学题重新进行另一种语言形式的表征，可实施不同数学模式之间的等价转换，进而为问题求解提供了多种通道.

例4 如图4，在△OAB中，OP∶PA=1∶2，OQ∶QB=3∶2，连接AQ、BP交于点R，过R作RH∥OA交AB于点H，若OA=1，OB=3，∠AOB=60°，求OH的长.

解析一：向量兼有几何与代数的双重特征，本题是用平面几何语言表述的，可用向量语言对之进行重新表述后，考虑求解方案.

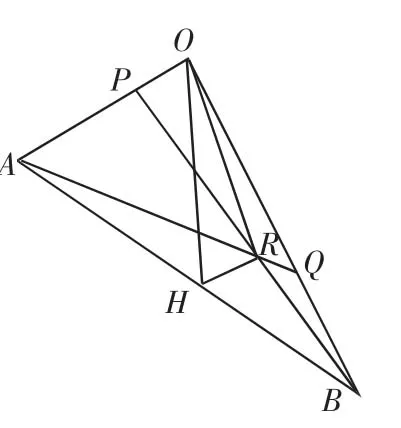
图4

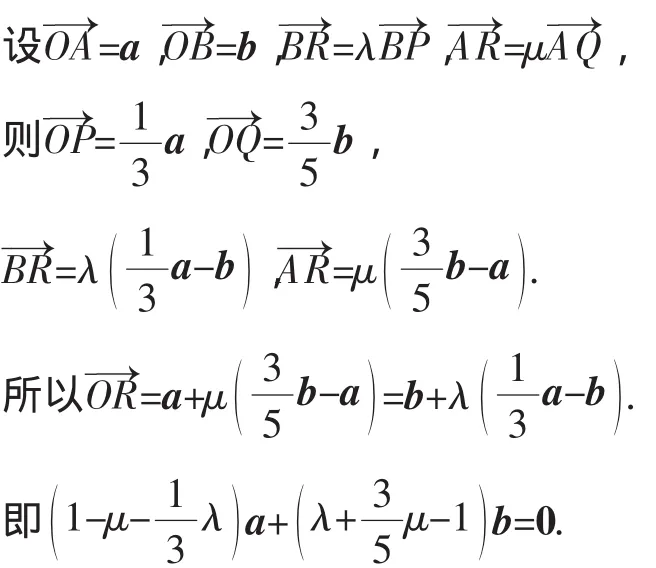
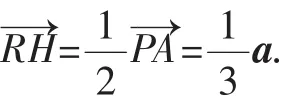
解析二：解析法也是处理平面几何问题的重要方法之一，用解析几何语言重新表述，将问题转化为解析几何问题求解，应该值得一试.

以O为坐标原点，直线OA为x轴建立直角坐标系，如图5.

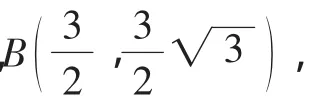
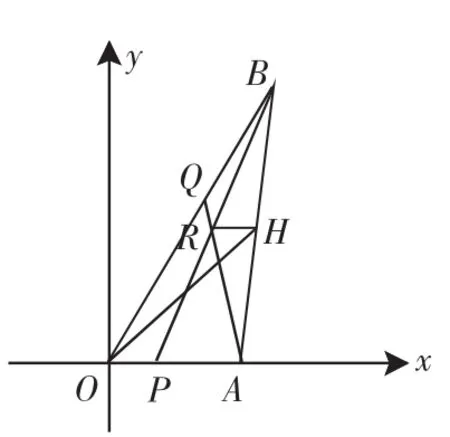
图5

注：本题也可用解三角形语言来表征，但需添加辅助线，请读者一试.

从上述四个“策略”成功运用的历程中，我们看到：自觉、主动地运用科学的思维策略，有助于快速确立解题思维的着力点，有利于找到解题的最近“攻击”方向，增强解题的目的性、可行性、创造性，避免解题过程中的盲目性、无效性、被动性.因此，在解题实践中，重视和加强思维策略的总结、积累与运用，是解题者学会怎样解题、提高分析问题和解决问题能力的必由之路.

1.（美）乔治·波利亚著.刘景麟、曹之江、邹清莲译.数学的发现：对解题的理解、研究和讲授［M］.北京：科学出版社，2006.

2.罗增儒.中学数学解题的理论与实践［M］.2008（9）.