探究一道竞赛题
2013-07-25 09:25江苏省常熟市中学查正开
中学数学杂志 2013年13期
☉江苏省常熟市中学 查正开

这是2011年西部奥林匹克数学竞赛第1题,参加这次竞赛的同学普遍感到此题较难上手.实际上,本题是一个贴近高考、背景公平、对称优美的竞赛题,学生解题困难是没有把握问题的本质,事实上,这道赛题源自人教版选修4-5教材中的一道不等式题.
习题:已知a,b,c∈R+,且a+b+c=1.
求证:(1-a)(1-b)(1-c)≥8abc.
分析:这道题目的证明,是运用二元均值不等式的一个典型范例.
证明:由a,b,c∈R+,a+b+c=1,结合均值不等式得:
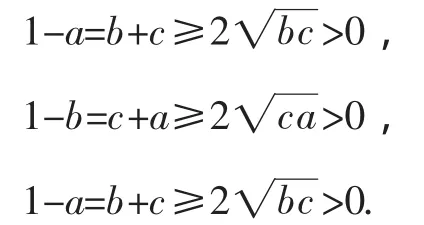
以上三式相乘即得(1-a)(1-b)(1-c)≥8abc.

在赛题中,令1-x-y=z,x+y=1-z,问题即为:

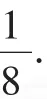
对这一赛题做进一步类比加强,利用换元结合两角和正切公式(高考重点内容),笔者编拟了一个类似问题,供同学们探究.
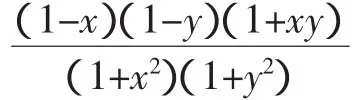

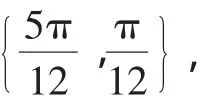
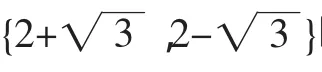
上式取等号,
由此可知,竞赛题和高考题均源自课本(或高于课本),我们只要透过表面现象,把握问题的本质,分析题目的结构特征,运用所学数学知识和方法,可以使很多看似复杂的问题得以顺利解决.
猜你喜欢
中等数学(2022年7期)2022-10-24
中等数学(2022年4期)2022-08-29
中等数学(2022年5期)2022-08-29
中等数学(2022年1期)2022-06-05
中等数学(2022年2期)2022-06-05
中等数学(2020年7期)2020-11-26
中等数学(2020年4期)2020-08-24
中等数学(2019年5期)2019-08-30
智富时代(2019年4期)2019-06-01
智富时代(2019年4期)2019-06-01

