小公式，大作用——从一道课本例题说起

☉江苏省扬州中学 陈黎黎

一、问题呈现

苏教版高中数学教材必修4第2.2.3节有这样一道例题：

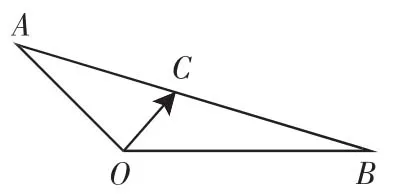
图1

原书证明过程如下：

此结论告诉我们什么？它在结构上有何特点？在向量的知识体系中占据什么样的地位？有着什么样的作用？笔者对它产生了兴趣，今作此文与读者探讨交流.

二、结论解读

定比分点的向量式与平面向量基本定理是特殊与一般的关系.平面向量基本定理中的基向量前的系数没有制约，而定比分点向量式的基向量前的系数和却等于1.由证明的过程不难发现这正是由A、C、B三点共线导致的.反之，该结论的逆命题也是成立的.（逆推结论的证明过程即得）

重新改写如下：

三、结论应用

1.系数和问题

此类问题中的若干向量以平面向量共线定理或平面向量基本定理的背景呈现（可能有三点共线的情境亦或没有），探寻向量表示的系数和的特征.

（1）三点共线情形：

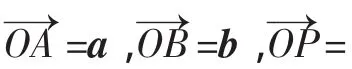
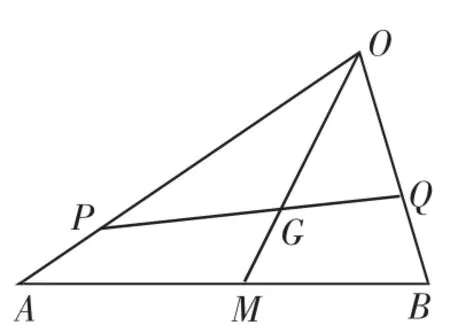
图2

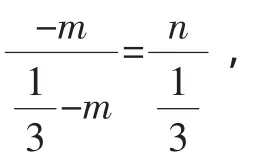
解后反思：问题中的m、n与点P、Q的位置有关，其值在变，但其倒数和为何为定值？

找到引发这一定值的本质原因才是真正理解并解决它的关键.P、Q在动，但这是在P、Q、G三点共线约束下的运动.动中有静—与定点G共线正是产生定值的本质原因！定值为3正是点G位置的体现！既然与三点共线问题有关，不妨考虑运用文中结论重解此题.

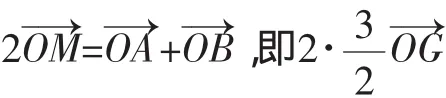
（2）无三点共线情形

这是近年高考向量命题的一个热点，通常需要解题者构作辅助线，转化为三点共线后再用此结论.

原解：设∠AOC=α，

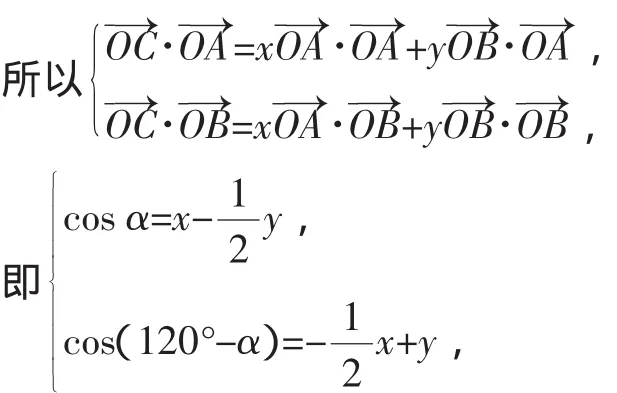
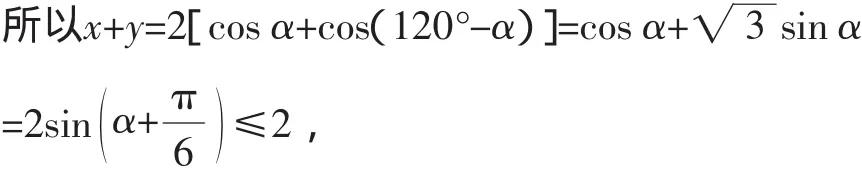
即（x+y）max=2.答案为2.

图3

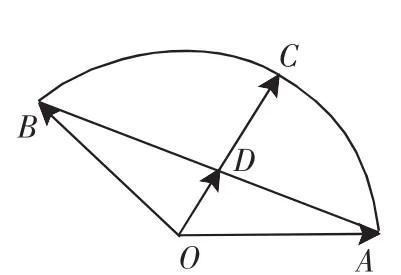
图4

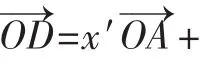
2.比值问题

此类问题一般会有一组或多组“X”形出现，这正是出现三点共线情形的一个表现.利用系数和的特点巧设向量可以找到突破口，从而迅速求出比值.

例3 如图5，设M为正方形ABCD的边AD的中点，以A为圆心，AB为半径的圆与以CD为直径的圆交于点P.N为BP与CD的交点，Q为AN与BM的交点，求证：

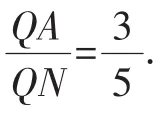
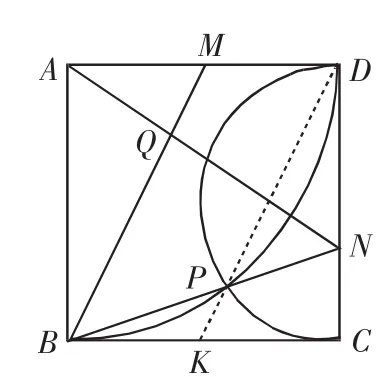
图5

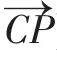
证明：如图5，连接DP并延长交BC于K，则

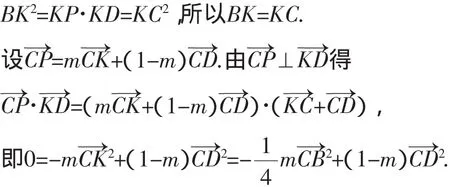
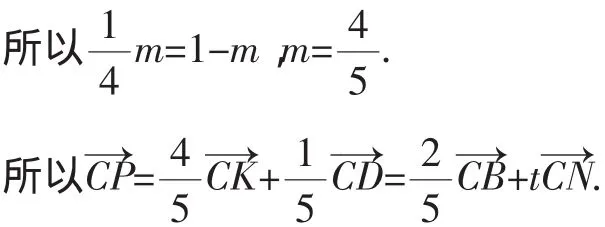
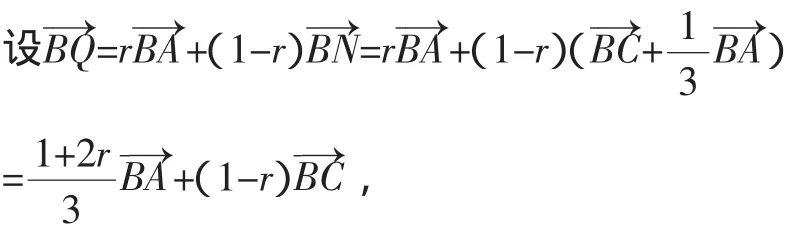
3.数量积问题

某些数量积问题若直接由定义运算，十分困难.此时不妨将数量积表达式中的向量用一组基底来表示（对于出现三点共线的情形，则可考虑运用定比分点公式的向量形式），之后再进行运算，可能会收到意想不到的效果.

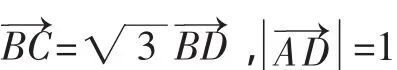
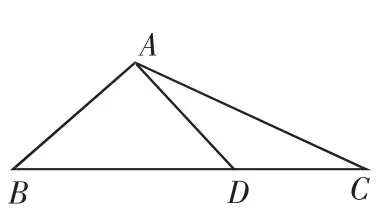
图6

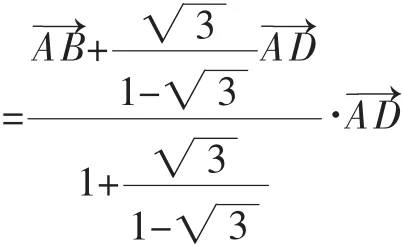
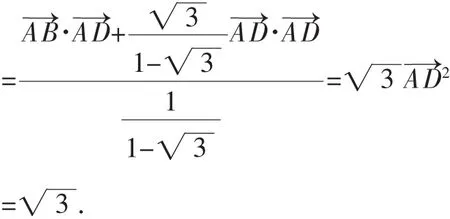
四、拓展延伸

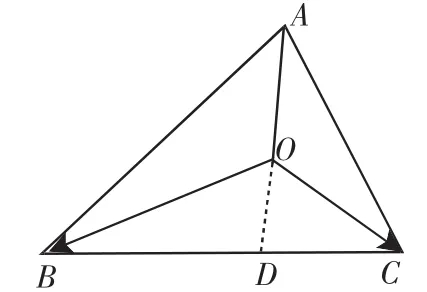
图7

证明：如图7所示，延长AO交BC于D.

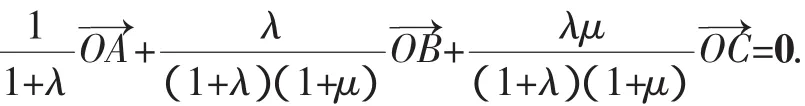
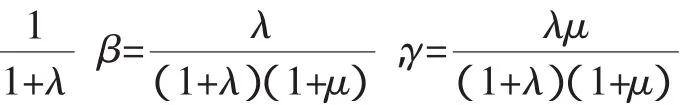
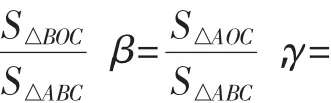
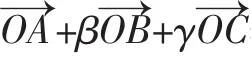
1.徐稼红.全日制普通高中课程实验教科书数学（必修4）［M］.南京：江苏教育出版社，2007.

2.张景中，彭翕成.绕来绕去的向量法［M］.北京：科学出版社，2010.

3.熊斌，冯志刚.高一年级奥数教程（第五版）［M］.上海：华东师范大学出版社，2010.