三向四次箱样条曲面与Bézier曲面的光滑拼接

杨联强，王 东

安徽大学 数学科学学院，合肥 230601

三向四次箱样条曲面与Bézier曲面的光滑拼接

杨联强，王 东

安徽大学 数学科学学院，合肥 230601

1 引言

箱样条（Box Spline）理论由de Boor和DeVore[1]开创，它以B样条和Bézier方法为其特例，将单变量样条推广到多元样条。在不同次数和定义域剖分方法的箱样条中，三向四次样条曲面由于其次数和连续阶之间良好的均衡（四次，C2连续），从而得以广泛重视和应用。著名的Loop细分曲面就是将三向四次箱样条曲面从正规三角控制网格推广到自由三角控制网格得到的。根据Stam[2]的网格参数化方法，Loop细分曲面的极限曲面几乎处处是三向四次箱样条曲面。

样条曲面适合于大范围连续曲面的构造，而Bézier曲面在设计单片曲面时却非常实用。Bézier方法形式简洁、性质优良，是计算机辅助设计（CAD）、计算机图形学（CG）中的基本工具[3]。实际应用中，需要在用样条曲面表示的大范围曲面上，添加局部的小曲面片，或用小曲面片“来补洞”[4]，此时，两曲面之间的光滑拼接就成为必须考虑的问题。因此，当三向四次箱样条曲面设计完成后，在其上添加Bézier曲面时，必须要考虑如何选取Bézier曲面的控制顶点以使得两曲面能光滑拼接。

有关曲面光滑拼接问题的研究成果已比较丰富。Du、Schmitt[5]对Bézier曲面的两片拼接及多边拼接作了比较完整的研究。施锡泉、赵岩[6]讨论了双三次B样条曲面的拼接条件。曲学军、宁涛、席平[7]介绍了基于调整已有曲面边界控制顶点的方法使得B样条曲面间实现G0、G1连续的方法。郝茹、刘润涛[8]给出了双四次有理Bezier曲面G1光滑拼接的顶点与权因子的相容条件。张锦秀、檀结庆[9]研究了H-Bézier曲面的G0、G1连续的相容条件。但是，目前这方面的研究主要集中于同种类型的曲面片之间的光滑拼接，而对不同类型的曲面片的光滑拼接的研究比较少。三向四次箱样条曲面与Bézier曲面光滑拼接的条件这一问题还未见有显式结果。本文针对这一问题，以多项式的Blossom为工具，讨论了在给定三向四次箱样条曲面，要设计与之C0、C1、C2拼接的Bézier曲面时，Bézier曲面的控制顶点所要满足的条件。

2 预备知识

关于三向四次箱样条的一般理论，详见文献[1，10]。单片的三向四次箱样条曲面可以表示为（如图1）：

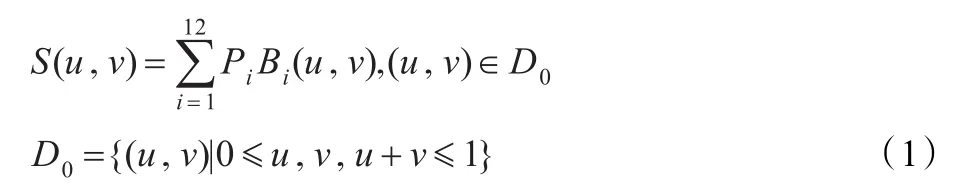
其中Pi是给定的ℜ3中的十二个控制顶点，Bi(u，v)是参数化后的三向四次箱样条基函数，其具体表达式可见文献[2，10]。简单计算可知三向四次箱样条曲面具有：

性质1单片的三向四次箱样条曲面是一张三边的二元四次多项式曲面片，其在某一边界上的0阶、1阶和2阶导矢都是与邻近该边界的十个控制顶点有关，而与较远的两个控制顶点无关。

记定义在参数域∆ABC上的n次三边Bézier曲面为T(u，v)，控制顶点为Qijk，i+j+k=n。记定义在参数域[a，b]⊗[c，d]上的张量积型双(m，n)次矩形Bézier曲面为R(u，v)，控制顶点为Rij，i=1，2，…，m;j=1，2，…，n，Bézier曲面具有：

性质2无论是三边还是矩形Bézier曲面，其在某一边界上的0阶、1阶和2阶导矢，分别由与该边界邻近的一行、两行和三行控制顶点决定，而与较远的控制顶点无关。

由于本文考虑三向四次箱样条曲面与Bézier曲面的光滑拼接，因此，取Bézier曲面的次数m和n都为4即可。

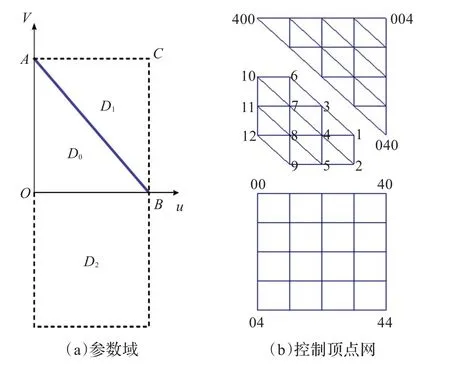
图1 三向四次箱样条曲面以及与其光滑拼接的三边和矩形Bézier曲面的参数域和控制顶点网

3 给定三向四次箱样条曲面，求与之光滑拼接的Bézier曲面

讨论如下问题：

在参数平面ℜ2上，给定由式（1）定义的三向四箱样条曲面S(u，v)，设：

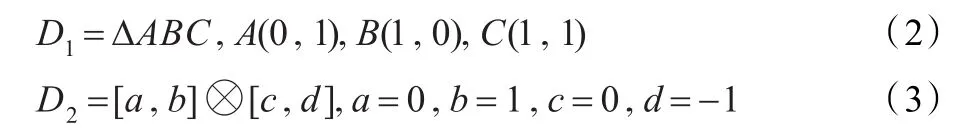
若定义在D1和D2上的T(u，v)和R(u，v)与S(u，v)分别C0、C1、C2拼接时，T(u，v)和R(u，v)的控制顶点应满足什么样的条件？

本文不采用通过分析两参数曲面在共同边界上的各阶导矢相等，从而得到控制顶点的相容条件这一方法，因为这种方法整理出的表达式比较复杂。而是使用多项式的Blossom这一工具，简洁巧妙地解决这一问题，直接给出由S(u，v)的控制顶点显式表示的Bézier曲面的控制顶点。

多项式的Blossom（Polar Form）由Ramshaw[11]于20世纪80年代首次提出。之后，众多学者利用这一方法对Bézier和B样条方法作出了一种全新的精妙解释，使得Blossom方法已成为研究Bézier和B样条的强大工具[3-4，12]。二元多项式的Bézier形式的Blossom有两种形式，分别在三角域和矩形域上进行，其具体的生成方法是用多元基本对称多项式来代替原多项式中的幂项，过程简单。在生成多项式的Blossom后，利用其对偶泛函性质，可以迅速求出该多项式在三角域和矩形域上的Bézier控制顶点。关于Blossom的生成及对偶泛函性质的应用，详见文献[4，12]。

下面给出解决问题的步骤：

首先，对已知的S(u，v)，这是一个二元四次多项式，分别生成它在三角域上的Bézier形式的Blossom，记作：

根据以上计算结果，得到如下定理：

定理1给定三向四次箱样条曲面S(u，v)，若定义在D1上的三边Bézier曲面T(u，v)的控制顶点满足式（7），则T(u，v)与S(u，v)C0拼接，若满足式（8）和式（9），则T(u，v)与S(u，v)C1拼接，若满足式（7）、（8）和（9），则T(u，v)与S(u，v)C2拼接。

证明 只证明C2拼接的情况，C0和C1时的情况更简单，不再赘言。

设想将多项式曲面S(u，v)的参数定义域延伸至区域D1上，记D1上的曲面部分Sˉ(u，v)：

定理2给定三向四次箱样条曲面S(u，v)，如果定义在D2上的矩形Bézier曲面R(u，v)的控制顶点满足式（10），则R(u，v)与S(u，v)C0拼接，若满足式（10）和式（11），则R(u，v)与S(u，v)C1拼接，若满足式（10）、（11）和（12），则 R(u，v)与S(u，v)C2拼接。

根据以上结果，分别给出了实例（图2、3、4）。中间位置曲面为三向四次箱样条曲面，而两侧曲面分别为与之C0、C1、C2拼接的三边和矩形Bézier曲面。

4 结论

以多项式Blossom为工具，给出了与三向四次箱样条曲面光滑拼接的三边或矩形Bézier曲面控制顶点的一个充分条件。当运用三向四次箱样条曲面造型，而需要构造Bézier曲面与之光滑拼接时，该结果能直接使用，具有很好的理论和应用价值。

当Loop细分曲面的控制顶点网在边界上没有奇异点时，曲面的边界即为三向四次箱样条曲面，应用本文结果可以解决Loop细分曲面与Bézier曲面的光滑拼接问题。当Loop细分曲面的控制顶点网在边界上有奇异点时，本文结果将不适用，此时，参照文献[13]，基于网格细分的两曲面间的光滑拼接问题的研究将是有意义的工作。

图2 三向四次箱样条曲面与Bézier曲面的C0拼接

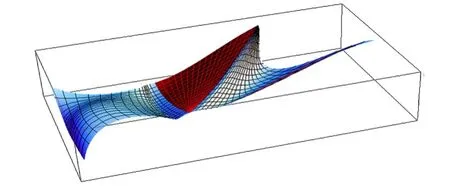
图3 三向四次箱样条曲面与Bézier曲面的C1拼接

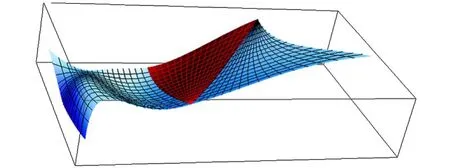
图4 三向四次箱样条曲面与Bézier曲面的C2拼接

[1]de Boor C，Hollig K，Riemenschneider S.Box spline[M].Heidelberg：Springer，1993.

[2]Stam J.Evaluation of Loop subdivision surfaces[C]//Computer Graphics Proceedings，Annual Conference Series，ACM SIGGRAPH，Orlando，1998：395-404.

[3]Farin G.Curves and surfaces in computer aided geometric design[M].5th ed.San Francisco：Morgan Kaufmann，2001.

[4]戈德曼.金字塔算法-曲线曲面几何模型的动态编程处理[M].吴宗敏，译.北京：电子工业出版社，2004.

[5]Du W H，Schmitt J M.On theG1continuity of piecewise Bezier surfaces：a review with new results[J].Computer-Aided Design，1990，22（9）：556-573.

[6]施锡泉，赵岩.双三次B样条曲面的G1连续条件[J].计算机辅助设计与图形学学报，2002，14（7）：676-682.

[7]曲学军，宁涛，席平.B样条曲面的光滑拼接[J].计算机辅助几何设计与图形学学报，2004，16（1）：138-141.

[8]郝茹，刘润涛.双四次有理Bezier曲面G1光滑拼接算法[J].计算机工程与应用，2010，46（4）：174-200.

[9]张锦秀，檀结庆.H-Bézier曲面的分割与拼接[J].计算机工程与应用，2011，47（9）：152-155.

[10]Chui C K.Multivariate splines[M].Philadelphia：SIAM，1988.

[11]Ramshaw L.Blossoming：a connect-the-dots approach to splines[R].California：Systems Research Center，1987.

[12]Goldman R N.Polar forms in geometric modeling and algebraic geometry[J].Contemporary Mathematics，2003，334：3-24.

[13]韩越兴，刘秀平，施锡泉.Loop细分模型的边界拼接算法[J].大连理工大学学报，2004，4（1）：12-16.

YANG Lianqiang,WANG Dong

School of Mathematical Science,Anhui University,Hefei 230601,China

Using bivariate quartic polynomial’s Blossom over triangular and rectangular domains,when a 3-direction quartic box spline surface is given,in order to make triangular or rectangular Bézier surface to beC0、C1、C2connected with it,one kind of explicit sufficient condition of the Bézier surface’s control points which should be subjected is discussed.When geometric modeling with 3-direction quartic box spline surface or Loop subdivision surface,this conclusion is valuable for making Bézier surface to be smooth connected with the modeling surface or to fill holes.

3-direction quartic box spline surface;Bézier surface;smooth connection

以二元四次多项式在三角域和矩形域上的Bézier形式的Blossom为工具，给出了当给定一张三向四次箱样条曲面时，能与之C0、C1、C2拼接的三边或矩形Bézier曲面的控制顶点所要满足的一个显式表示的充分条件。这一结果在使用三向四次箱样条曲面或Loop细分曲面造型，而又需要构造Bézier曲面与之拼接或补洞时，具有理论和实际应用价值。

三向四次箱样条曲面；Bézier曲面；光滑拼接

A

TP391.7

10.3778/j.issn.1002-8331.1303-0387

YANG Lianqiang,WANG Dong.Smooth connection between 3-direction quartic box spline surfaces and Bézier surfaces. Computer Engineering and Applications,2013,49（23）：119-121.

国家自然科学基金数学天元基金项目（No.11026076）；安徽大学博士科研经费项目（No.31190016）；安徽大学本科生科研训练计划（No.KYXL20110003）。

杨联强（1975—），男，博士，副教授，主要研究领域为计算机辅助几何设计；王东（1991—），男，本科生。

2013-03-25

2013-05-30

1002-8331（2013）23-0119-03

CNKI出版日期：2013-08-27 http://www.cnki.net/kcms/detail/11.2127.TP.20130827.1603.014.html