动态环境中的多机器人协同搬运

曹 洁，朱宁宁

兰州理工大学 计算机与通信学院，兰州 730050

动态环境中的多机器人协同搬运

曹 洁，朱宁宁

兰州理工大学 计算机与通信学院，兰州 730050

1 引言

多机器人系统是一个集环境感知、动态决策、行为执行等多功能的复杂系统。随着多机器人在工业生产、医疗服务、航空航天等方面的应用，多机器人协作成为机器人学研究的热点。而多机器人协同搬运问题无论是在理论层面还是在应用上都有着非常广阔的研究价值，一方面在真实的物理世界中，单个机器人通常无法完成很多任务，另一方面，它也是研究多机器人协同任务的一个重要平台[1]。

针对多机器人的避障问题，已经提出了很多的方法，如模拟市场法、栅格法和基于行为的控制方法等。基于行为的控制方法由著名人工智能专家R.Brooks首先提出来，较于传统方法，具有鲁棒性好、快速性[2]等优点而得到广泛关注。由于多机器人工作环境的易变性和不可预见性，需要多机器人尽可能的适应环境，以提高学习和决策能力。Q学习[3-4]无需建立环境模型，且可在线学习，被用于多机器人避障问题中，但是，并不十分理想。这是因为随着多机器人数量增加，学习空间也快速增大，造成了学习速度非常缓慢，且环境信息不完备时，联合学习模型也难以适用。有学者将Q学习中的“状态-动作对”替换为“条件-行为对”，虽具有一定的有效性，但还是无法克服此问题；分布式两层强化学习算法也被用于多机器人协作中，实验验证了其实际功能，但仍无法较大地减小存储空间；将基于动作预测的强化学习算法用于多机器人协同搬运问题会大大促进协作性能，缺点是在环境信息较少或者机器人存在自私目标的情况下难以适用。Q学习是通过奖励值来强化正确的行为，它是一种数值分析方法，此方法忽略了多机器人的推理能力，而引入BDI模型能够有效解决Q学习推理能力较弱的弊端[5-6]，因此本文中的多机器人采用基于BDI模型的独立强化学习，使得多机器人学习过程不仅拥有强化学习的自适应性和高度反应性，而且拥有了推理功能。

本论文的创新点有：（1）本文将强化学习算法、BDI模型、基于行为的协同方法三者结合运用于多机器人协同搬运问题，并从仿真实验看，取得了较好的效果。（2）本文采用强化学习的评价函数是随多机器人系统位置及离最近障碍物距离而变化的，评价函数可实时更新，并将其与基于强化学习的行为权重相结合，都使得本实验取得良好仿真效果。

2 Q(λ)学习算法

马尔可夫决策过程[7]中，多机器人所处的环境状态表示为状态集合动作集合描述为多机器人在状态st下，选择动作at并且执行。同时，状态转换为st+1，然后从环境中得到了强化信号rt。

Q学习是一类被广泛应用的强化学习算法[8]，它用函数Q(x，a )表达与各个状态相对应的动作的评估。其表达式为：

由于强化学习系统的目的是使得总的奖励值达到最大，因此，用可得：

在时刻t，多机器人根据当前的状态选择一个动作a，然后，根据以下表达式更新Q值：

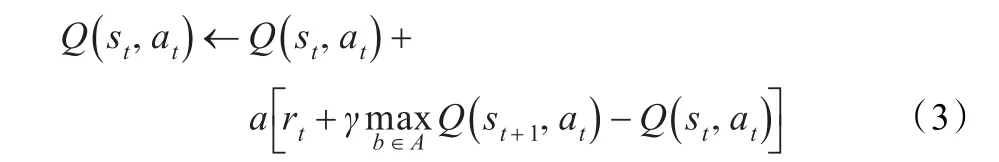
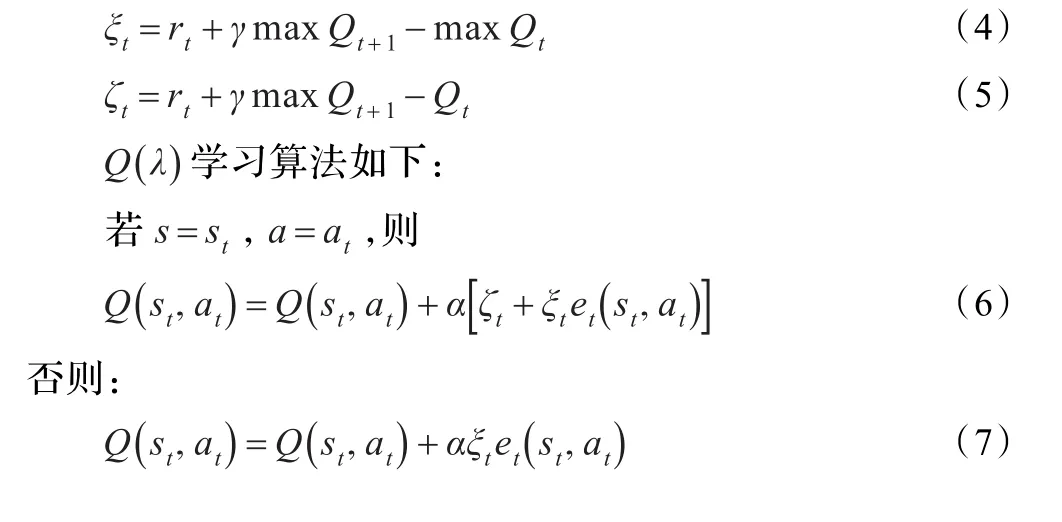
3 基于强化学习的BDI协作模型

“信念-愿望-意向”（BDI）多机器人系统根据内部的心智状态产生动作进而影响周围环境。BDI多机器人系统有3个主要心智状态：信念（belief），愿望（desire）和意向（intention），分别代表多机器人所具有的信息、动机和决策。而在多机器人BDI模型中，信念代表多机器人对当前的环境与自身可能要采取的行为估计；愿望代表多机器人对未来环境与自身可能要采取行为的喜好；意向代表多机器人为了达到某个目的做出的承诺。

BDI Robot的求解意见过程驱动手段-目的的推理，同时还需要满足几个其他的约束：产生的意见必须和Robot当前的信念及意图一致；其次，应能识别环境变化的趋势，提供Robot获得意图的新方法或者新的可能性。一个BDI Robot慎思过程用过滤函数表示，过滤函数根据Robot当前的意图、信念和愿望来刷新Robot的意图。它需要丢弃无法完成的或者已经无意义的意图，为不能实现的意图选择新的实现方法及意图。

在多机器人系统体系结构中可由E（环境）引起最初的变化。当环境变化时，机器人将收到新的信息来更新自身的bel（信念）。通过环境感知函数sence，机器人可感知到环境的变化。每当环境发生变化，机器人将及时更新自身的bel（信念）以满足新的变化的要求。机器人的bel是在开放的环境下，处于动态变化之中。Bel变化将引起des（愿望）变动，des变动会影响int（意向）的选择及要采取的行为，最终影响整个环境发生变化。机器人的变动为一种链式反应，E变化引起bel、des和int变化，最终又影响到E。

此动态模型的具体定义：

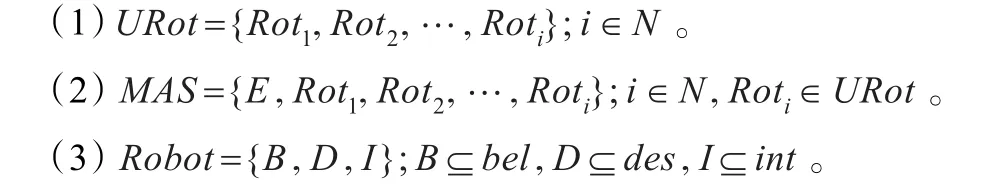
（4）感知函数sence：ρ(bel)×e→ρ(bel)，该函数跟据当前对环境的感知和信念确定新的信念集合。

（5）意见函数opinion：ρ(bel)×ρ(int)→ρ(des)，该函数跟据当前环境的感知和意图的执行确定一个新目标。

（6）过滤函数filter：ρ(bel)×ρ(des)×ρ(int)→ρ(int)，该函数依据Robot当前的意图、信念及愿望更新Robot的意图。

（7）行为函数action：Roti×ρ(int)→Roti×E，若i=j为内部行为，若i≠j，则为外部行为。

{S，G，R，B，D，I，λ}中，S为离散的状态空间，G为协同求解的目标，R为多机器人的集合，B为多机器人的信念集合，D为多机器人的愿望集合，I为多机器人的意图集合，λ={λ1，λ2，…，λn}为多机器人问题求解时的价值系数集合，λ∈(0，1)。通常情况下，由于每个Robot都是依据自身的局部规划来进行局部求解，却不考虑其他Robot的动作规划，因此Robot之间必然会存在意图冲突，从而使式（8）成立：

意图是多机器人系统的内部动力，而不稳定性主要源于意图冲突。由动力学理论，系统的运动总趋向稳定平衡态而远离不稳定平衡态。针对多机器人系统，不管是协作还是冲突，最终总要达到某个稳定点或平衡点。如果将系统内的多机器人分为两部分：意图有冲突的Robot与意图无冲突的Robot，则可把系统看作双矩阵对策系统。依据Nash定理，它必然存在混合策略平衡。若假定所有Robot学习同一个Nash平衡，这将使得每一个Robot的选择能够最优地响应其他Robot的选择，因此式（9）得以成立：

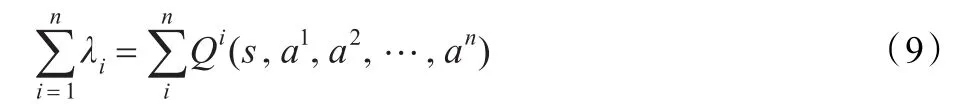
这样在系统中，所有Robot能够追求共同最优解，即追求最大限度地实现整体联合意图。

信息完备时，联合学习模型能有效实现多机器人协作，但当机器人得不到完整信息时，此方法难以使用。在信息不完备的情况下，多机器人采用独立学习的方式。机器人不知道其他机器人的行为策略，每个机器人进行独立学习，它依据自身得到的奖励维护状态动作对的Q值表，每一Q值表示某个优化策略在此状态动作对的奖励值。已有文献[9]证明了信息不完备时采用此规则进行独立强化学习能使得多机器人协作决策过程得以收敛。多机器人之间不能交互行为策略时，某一状态，多机器人依据Q值表执行动作，且根据反馈得到的奖励值更新Q值表。

BDI模型通过形式化心智成分和逻辑推理实现多机器人行为的自主性和理性，强化学习通过感知环境状态和得到的奖励值学习系统的最优行为策略。单独使用符号推理的逻辑方法无法使得效用最佳，而数值分析的强化学习也忽略了推理的环节，对于多机器人系统来说，既需要对于环境信息推理，又要经过学习不断地强化正确行为使之得到最大的收益，因此，将强化学习和BDI模型结合起来研究多机器人协作问题。

3.1 基于权重的行为机制

搬运物体分为两个部分：（1）躲避障碍物；（2）向目标区域前进。在整个多机器人的协同搬运中，都是由这两个行为组成，但是，每个行为重要性是不同的。描述为：

其中，Weightavoid和Weightbin是躲避障碍物和向目标区域前进的权重。MS-AVOID-OBSTACLES、MS-MOVE-TO-OBJECTBIN分别代表躲避障碍物、向目标区域前进两个行为。

3.2 基于强化学习的行为权重

多机器人协同搬运过程中，不同的行为具有各自的权重，且在不相同的环境中各行为的重要性也有区别，为了能够使得行为权重依据环境自动进行调整，采取了强化学习自动学习理想的权重组合，以使得机器人能够像人类一样的学习，完成协同搬运过程。

学习初期，各行为权重都设有初始值，学习过程中，根据环境反馈的信息，运用评价函数r对权重评价，当完成一次协同搬运后，此权重就会被重新进行计算：

若完成协同搬运过程，则r为正，就使得当前权重值增大；当未完成时，r为负值，使得当前权重值减小。评价函数定义为：

式中，xavg表示在tmin时间间隔内，多机器人系统的位置；xt表示最近障碍物的位置；a是安全阈值。

3.3 距离最近原则的多机器人协同搬运

距离最近原则即为在全部协同搬运的多机器人中，选择距离障碍物最近的机器人作为主机器人，由其发出指令进而控制其他的机器人执行动作。如式（12）。在搬运过程中，设离障碍物最近的作为主机器人，指挥其他从机器人行动。

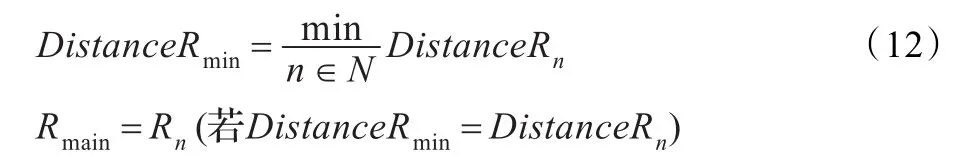
其中，Rmain为主机器人，Rn为n号机器人，DistanceRmin为机器人距离障碍物最近的距离，DistanceRn为机器人N到障碍物的距离。

4 仿真实验

4.1 实验场景

为了验证将BDI模型和强化学习相结合引入多机器人协同搬运过程的有效性，在仿真环境下对其进行验证。四个机器人站在两两互成90°角的等分点上抬着圆桶在如图所示的障碍物环境中，将圆桶搬运至目的地，本次实验任务假定该物体是密度分布均匀的，实验环境如图1所示，实心物体代表障碍物，空心圆代表整个多机器人系统及圆桶的出发地。

图1 障碍物、目标区域位置设置

其中，出发地内圆桶与四个机器人的位置分布放大图如图2所示，虚线代表出发地，空心圆代表圆桶，四个实心圆分别代表四个机器人。

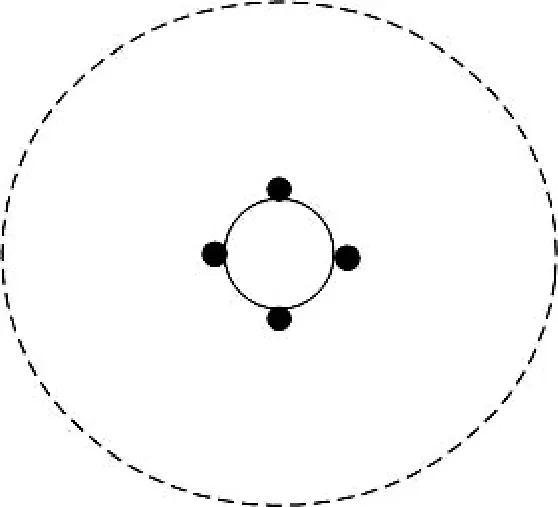
图2 出发地内四个机器人与圆桶的位置放大图

4.2 强化学习单元

（1）评价函数的表示

在多机器人协同搬运过程中，各子行为初始权重分别设置为Weightavoid=1，Weightbin=1，各权重相应的强化学习评价函数如下：

（2）状态空间的表示

多机器人系统的状态空间S：

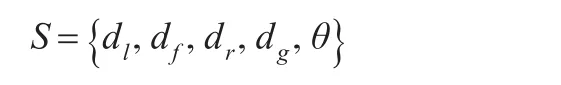
其中，dl是多机器人系统左侧距障碍物的距离，df是多机器人系统前方距障碍物的距离，dr是多机器人系统右侧距障碍物的距离，dg是多机器人系统与目标点之间的距离，

θ是多机器人系统当前方向与目标点的夹角。用这5个量作为状态空间的5个维度，多机器人系统和障碍物的距离定义

（3）动作空间的表示

多机器人系统的动作空间A：

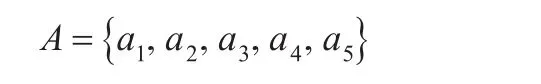
其中，a1为机器人转动+15°同时前进；a2为机器人转动-15°同时前进；a3为机器人转动+10°同时前进；a4为机器人转动-10°同时前进；a5为机器人前进。

t时刻多机器人系统的状态St为一个五维向量：

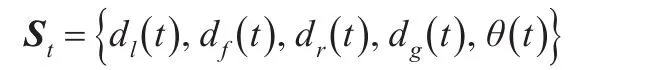
4.3 动作选择策略

学习的初始阶段，因其Q值是随机初始化，所以不具任何意义。为了探索到全部可能的动作，引入Boltzmann分布实现初始阶段动作的随机选择，某个动作被选择的概率为：

图3 机器人、障碍物和目标点的位置图

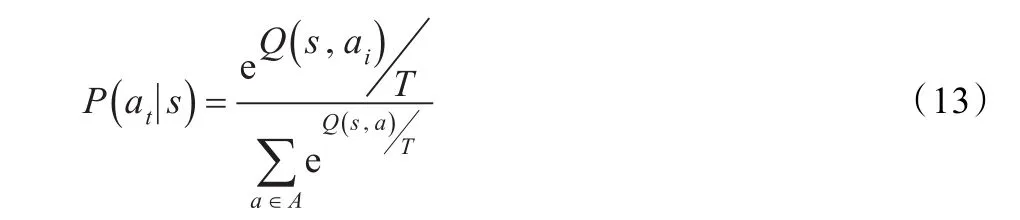
式中，T为虚拟温度，随着温度增加，选择的随机性也加强。

随着学习的进程，Q值慢慢趋向于所期望的状态-动作值，此时，根据贪婪策略选择动作，即选择最大的Q值对应着的动作。

为了显示出强化学习算法与BDI模型结合的有效性及优越性，共进行了三次实验：

（1）原始强化学习算法用于多机器人协同搬运，如图4所示。

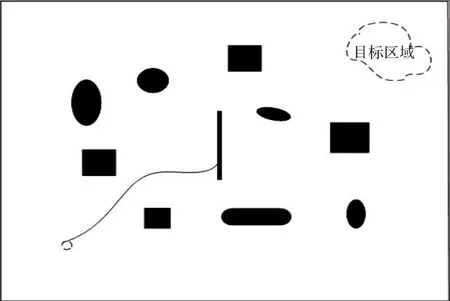
图4 原始强化学习算法用于多机器人协同搬运轨迹图（多次学习后）

（2）强化学习与BDI模型用于多机器人搬运（学习初期），如图5所示。

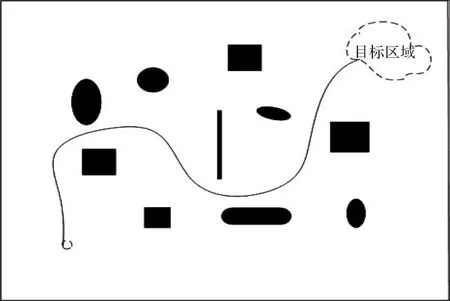
图5 强化学习与BDI模型用于多机器人搬运轨迹图（学习初期）

（3）强化学习与BDI模型用于多机器人协同搬运，如图6所示。

图6 强化学习与BDI模型用于多机器人协同搬运轨迹图

并且，比较了强化学习-BDI模型结合与原始强化学习算法的循环次数与成功次数的效果，如图7所示。

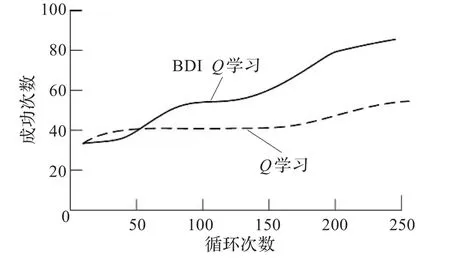
图7 循环次数与成功次数的仿真结果

4.4 实验结果与分析

由图4和图7可以看出，原始强化学习算法在多机器人协同搬运过程中，经过较多次学习，机器人还是总与障碍物相撞，这是因为强化学习算法存储空间很大，学习速度很慢，并且不具备推理能力，在环境信息不完备的情况下，联合学习模型难以适用；将BDI模型与强化学习结合起来用于多机器人协同搬运时，多机器人系统在一个存在随机设置障碍物的环境中运行，在初始阶段，由于多机器人处于随机选择动作的阶段，因此运行中路线不平滑；但是经过多次学习后，多机器人能够实现在躲避障碍物的条件下顺利到达目标区域，并且运行轨迹比较平滑。随着学习的持续，运行效果也越来越好。这是因为BDI模型的引入能够有效解决强化学习推理能力弱的问题。

5 结束语

将多机器人系统的独立强化学习与BDI模型相结合，使得多机器人系统不仅具有强化学习的自适应性和高度反应性，而且也拥有了BDI模型的推理能力，这就使只用数值分析却忽略推理环节的强化学习方法结合了逻辑推理方法。在使用此方法后，有效地减少了多机器人系统与障碍物发生碰撞的次数，增大了实现协同搬运的成功率，具有良好的学习效果。仿真结果也表明了此方法的有效性，可以满足多机器人系统的要求。本文主要是把此方法用在静障碍物的情形下，今后的工作是把此方法应用到更为复杂的环境中，实现更多的功能。

[1]Bauer A，Wollherr D，Buss M.Human-robot collaboration：a survey[J].International Journal of Humanoid Robotics，2008，5（1）：47-66.

[2]Jan G E，Chang K Y，Parberry I.Optimal path planning for mobile robotnavigation[J].IEEE-ASME Transactionson Mechatronics，2008，13（4）：451-460.

[3]Busoniu L，Babuska R，De Schutter B.A comprehensive survey ofmultiagentreinforcementlearning[J].IEEE Transactions on Systems，Man and Cybernetics，2008，38（2）：156-172.

[4]Hwang K S，Ko Y C，Alouini M S.Performance analysis of incremental opportunistic relaying over identically and nonidentically distributed cooperative paths[J].IEEE Trans on Wireless Commun，2009，8（4）：1953-1961.

[5]朴松昊，孙立宁，钟秋波.动态环境下的多智能体机器人协作模型[J].华中科技大学学报，2008，36（10）：39-52.

[6]樊建，郑昌陆，费敏锐.基于角色变换和强化学习的多机器人协同仿真[J].系统仿真学报，2009，21（21）：6964-6967.

[7]颜振亚，郑宝玉，林志伟.无线传感器网络中机会协作传输及其性能研究[J].电子与信息学报，2009，31（1）：215-218.

[8]Gosavi A.Reinforcement learning：a tutorial survey and recent advances[J].INFORMS Journal on Computing，2009，21（2）：178-192.

[9]Juang C F，Hsu C H.Reinforcement interval type-2 fuzzy controller design by online rule generation and Q-value-aided antcolony optimization[J].IEEE Transon Systems，Man and Cybernetics Part B，2009，39（6）：1528-1542.

CAO Jie,ZHU Ningning

College of Computer and Communication,Lanzhou University of Technology,Lanzhou 730050,China

In the multi-robot cooperative carrying process,traditional reinforcement learning only uses numerical analysis and ignored reasoning approach.To solve this problem,independence reinforcement learning for multi-robot combines with Belief-Desire-Intention（BDI）model,which makes reinforcement learning link logical reasoning capabilities.And the distance nearest principle is employed which means that the nearest robot ranged from obstacles is the leader robot to control other robots move.Evaluation function which changes with the location of multi-robot and the barriers is proposed,and it combines with the behavior weight based on reinforcement learning which becomes more and more optimized through constantly interacting with the environment.Simulation results show that this method is feasible,and the cooperative carrying process can be successfully achieved. Key words：multi-robot;reinforcement learning;cooperative carrying;obstacle avoidance

在多机器人协同搬运过程中，针对传统的强化学习算法仅使用数值分析却忽略了推理环节的问题，将多机器人的独立强化学习与“信念-愿望-意向”（BDI）模型相结合，使得多机器人系统拥有了逻辑推理能力，并且，采用距离最近原则将离障碍物最近的机器人作为主机器人，并指挥从机器人运动，提出随多机器人系统位置及最近障碍物位置变化的评价函数，同时将其与基于强化学习的行为权重结合运用，在多机器人通过与环境不断交互中，使行为权重逐渐趋向最佳。仿真实验表明，该方法可行，能够成功实现协同搬运过程。

多机器人；强化学习；协同搬运；避障

A

TP242

10.3778/j.issn.1002-8331.1202-0215

CAO Jie,ZHU Ningning.Multi-robot cooperative carrying in dynamic environment.Computer Engineering and Applications,2013,49（23）：252-256.

曹洁（1966—），女，博士生导师，教授，主要研究领域为智能交通系统、信息融合理论及应用；朱宁宁（1986—），女，硕士。E-mail：307516638@qq.com

2012-02-13

2012-03-23

1002-8331（2013）23-0252-05

CNKI出版日期：2012-06-15 http://www.cnki.net/kcms/detail/11.2127.TP.20120615.1726.038.html