改进的QPSO-BP算法的铀价格预测模型及应用
陈建宏,周汉陵,于凤玲,杨珊
中南大学资源与安全工程学院,长沙 410083
改进的QPSO-BP算法的铀价格预测模型及应用
陈建宏,周汉陵,于凤玲,杨珊
中南大学资源与安全工程学院,长沙 410083
1 引言
铀是核电站反应堆燃料和核武器材料,在我国国民经济和国防安全中占重要的地位。铀产品价格的变化直接决定了铀矿项目的价值,预测铀产品价格的变化,可以提高企业的经营决策能力和抗风险能力[1]。目前,国内学者对铀产品价格变化进行了大量的研究。彭新建、周云忠等[2-4]从铀库存释放和二次铀资源供应、市场需求定性分析了铀价格的走势。张海伦[5]探索并建立了铀供应与需求曲线,构建了用于铀价格分析的框架。张坤等[6]运用了古典经济学的供求关系基本理论,以铀产量及核反应堆作为国际市场铀供需双方的代表性指标,对铀价格变动的机制展开了分析。
这些方法能运用经济学理论对铀产品的价格趋势进行预测,铀价格影响因素多且复杂,用供需理论无法准确揭示铀产品时间价格的变化中复杂的动态化非线性规律[7]。随着计算机技术的发展,研究者将人工智能的预测方法如BP神经网络、支持向量机[8]等运用到价格预测中来,赵玉、丁睿等[7,9]利用改进的神经网络,预测了国际铀资源的价格,这些方法对于复杂的因素具有较强的拟合能力。
但是利用BP神经网络时,存在容易陷入局部最小以及收敛速度慢等问题。很多研究者将混合神经网络如遗传神经网络[10-11]、粒子群神经网络[12-13]运用到股票、黄金价格等的预测中,利用进化算法提高了神经网络的泛化映射能力以及加快了网络的收敛速度。量子粒子群算法是在对粒子群收敛性的基础上提出的群体智能优化算法,对粒子群早熟收敛、寻优能力较差、收敛速度较慢等问题进行改进。本文以某铀业发展有限公司Millennium(千禧年)项目提供铀(U3O8)价格数据为基础,改进的量子粒子群算法优化BP网络的训练过程,提高预测结果的精度。网络泛化能力与稳定性优于粒子群优化BP模型与传统BP模型。通过对铀价格进行精确预测,为铀资源技术经济评价以及矿业风险投资提供决策依据。
2 基于改进的量子粒子群优化算法神经网络训练方法
2.1 基于改进的量子粒子群优化算法
量子粒子群优化(Quantum-behaved particle swarm optimization)算法[14]是一种基于群智能全局优化的技术,在量子空间中,粒子聚集性是通过其运动中心的吸引势产生的束缚态进行描述的,束缚态下的粒子以一定的概率密度在空间任何点出现,满足聚集态的粒子能在整个可行解的空间进行搜索,且不会发散至无穷远处,从而找到最优解。
基于δ势阱的量子粒子群算法(QPSO)首先用波函数Ψ(X,t)来描述粒子的状态,其中,X为粒子i的三维空间位置向量,波函数的模的平方等于粒子在空间中某一点出现的概率密度。然后采用逆变换法(蒙特卡罗法)得到粒子的位置方程:

其中,t是离散时间,L是δ势阱的特征长度,收敛点p在实际的算法运行中为随机变量,u(t)是在(0,1)上的均匀分布。
将上述结果扩展到N维的搜索空间,对于粒子i(粒子位置坐标xi,j,j=1,2,…,N),第j维的坐标的基本进化方程为:

传统QPSO将参数α随时间变化,从1线性减小到0.5。随着时间t的增加,粒子经历个体的最优位置pbest逐渐接近群体最佳位置gbest,平均最好位置mbest与每个粒子位置的差距也将逐渐变小,导致粒子实际搜索范围减小,粒子群进化趋于停滞。本文采用文献[15]提出的方法,将α 从0.6增加到0.9,延缓整个粒子群存在的早熟趋势。

其中,maxiter为最大迭代次数。
在算法的搜索后期,即使α增加至0.9,仍有粒子所经历的pbest与gbest十分接近,导致δ势阱的特征长度L很小。因此,针对每个粒子,本文采用文献[16]中的第二种方法,对参数L进行改进。

2.2 BP神经网络
BP神经网络是一种基于误差的反向传递(back propagation)算法。结构图如图1所示。

图1 BP神经网络的拓扑结构
在训练BP网络时,给定样本输入向量I,实际输出向量D可以表示为:

其中,W是链接权值的矩阵,V是阈值向量;f为S型函数或者线性函数。
给定目标输出向量T,将误差函数作为适应度函数fitness,可表示为:
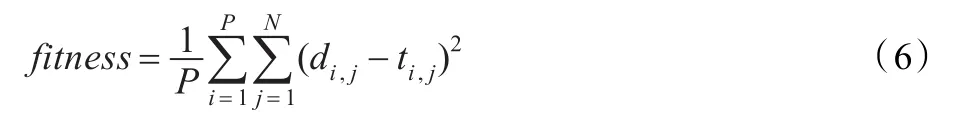
其中,P为样本总数,N为输出节点数,di,j,ti,j分别是第i个样本的第j个输出节点的实际输出和目标输出。
神经网络外推能力用泛化能力来进行评价。泛化能力是指衡量预测值与实测值之间差别的变量,用平均相对变动值(Average Relative Variance,ARV)表示[17],ARV值越小,网络泛化能力越强。

2.3 基于改进的QPSO-BP算法流程
BP神经网络学习的过程主要是权值和阈值更新过程,将网络权值与阈值进行编码成粒子群位置向量,则每一个粒子代表了网络的一组权值与阈值,以误差函数作为改进QPSO算法适应度函数,通过优化搜索得到满足适应度函数值最小的一组粒子,即为训练网络的一组最优的参数。其基本流程为:
(1)给定输入向量和期望输出向量:
①数据划分。采用滚动的方式对样本进行重构,即前N个值来预测后M个原始序列的值。数据划分方法见表1。

表1 数据划分
②原始数据序列x(t)归一化。min(t)与max(t)分别是数据序列中的最小值与最大值。

(2)确定神经网络输入层、隐含层、输出层节点数。
(3)粒子群初始化。设定粒子数M,粒子向量X的长度L、目标适应度值fitness、最大迭代次数maxiter和粒子速度向量维数D。
①粒子数。对于一般优化问题,粒子数取20~40即可得到较好的结果。
②粒子向量X的长度L。计算公式为:L=(s1+s3)× (s2+1),其中,s1为输入样本的维数,s2为隐含层节点数,s3为输出结果维数。
③粒子维度。其值与神经网络的连接权值与阈值有关,计算公式为:D=w+ν+h+n,w=m×h,ν=h×n,其中,D为速度向量的维数;w为输入层到隐含层的连接权值的个数;ν为隐含层到输出层的连接权值的个数;m为输入层节点数;h为隐含层节点数;n为输出层节点数。迭代次数N初始值为1。
(4)适应度函数的确定。用公式(6)计算适应度函数fitness,来评价粒子的搜索性能。
(5)当种群的最优适应度值满足目标适应度值或达到最大迭代次数时,学习过程结束;否则,令N=N+1,返回步骤(4)继续迭代。
(6)设置网络的训练误差最大值g。若fitness〉g,则采用所得连接权值与阈值作为网络训练的初始值,然后用训练好的网络对新输入的样本进行预测;若fitness≤g则直接对新样本数据进行预测。
3 基于量子粒子群优化的神经网络在铀矿价格预测中的应用
在MAΤLAB R2010a的环境进行实验,为了提高预测的效率,将训练与预测过程设计成一个程序。数据来自某铀业发展有限公司Millennium(千禧年)项目提供的铀(U3O8)2004年5月至2011年5月的价格数据,见表2。

表2 预测模型的训练样本
3.1 构建模型
将表2样本集的数据,按照表1进行数据划分,令N=5,K=75,M=1,分为80个长度为6的数据段,按公式(8)对数据进行归一化处理;网络输入节点数为5,根据隐含层数量公式:ni=2n+1,选择隐含层节点数为11,输出节点为铀价预测值,因此,网络结构为5-11-1型;训练和测试网络的过程中,训练样本的组数越多,可以提高网络的预测精度,即前75组数据作为训练的样本,后5组数据作为测试的样本。将样本处理后输入至网络进行训练。
3.2 QPSO优化BP网络
由神经网络5-11-1型结构确定需要优化的参数为1 560个,即

取粒子数目为20,粒子向量X的长度L为66,粒子速度向量维数为78;最大迭代步数100。参数优化过程如图2所示。阈值、优化后的粒子位置向量、由向量解码成的网络权值如下:

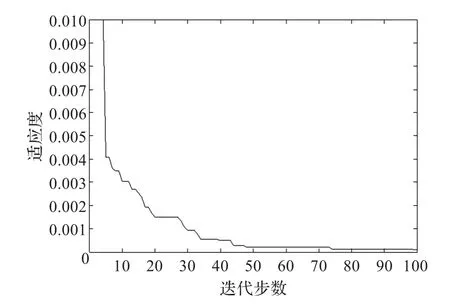
图2 适应度优化曲线

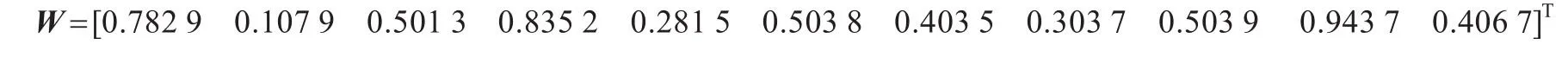
QPSO适应度优化曲线和PSO适应度优化曲线如图3,图4所示。

图3 QPSO适应度优化曲线
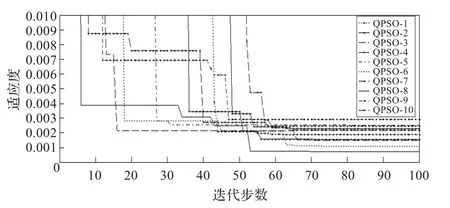
图4 PSO适应度优化曲线
3.3 预测结果
将用QPSO优化后的网络参数代入BP神经网络,作为参数的初始值,满足训练精度或最大训练次数后,进行预测。从表3中可以看出,模型预测结果的相对误差的绝对值最大为0.67%,最小为0.10%。预测结果较好,但是具有一定的随机性。
为了进一步检验QPSO-BP模型在预测中的有效性,采用平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)来衡量预测精度。另外做了3组实验(参数设置见表4),分别用三种模型进行预测,每组10次。对比三种网络预测结果(表5,鉴于篇幅有限,只列出每个模型每组的第一个预测值)与多次实验的结果(表6)。结果表明,实验1:QPSO-BP模型的MAPE均值为0.151%,最大精度为0.26%。实验2:PSO-BP模型的MAPE均值为4.553%,最大精度为7.81%。实验3:未经过优化的BP模型MAPE均值为30.86%,最大精度为41.23%。显然,QPSO的预测精度较好。
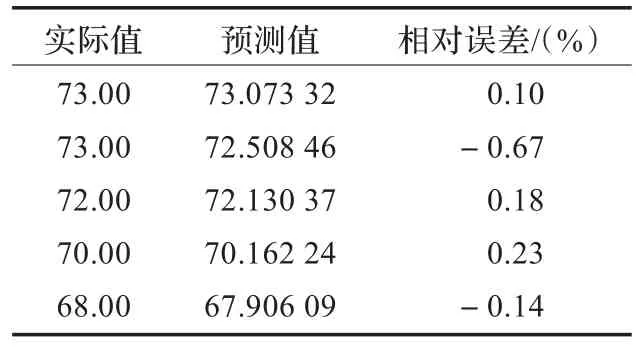
表3 QPSO-BP模型预测结果

表4 PSO与QPSO参数设置

表5 三种模型预测值比较
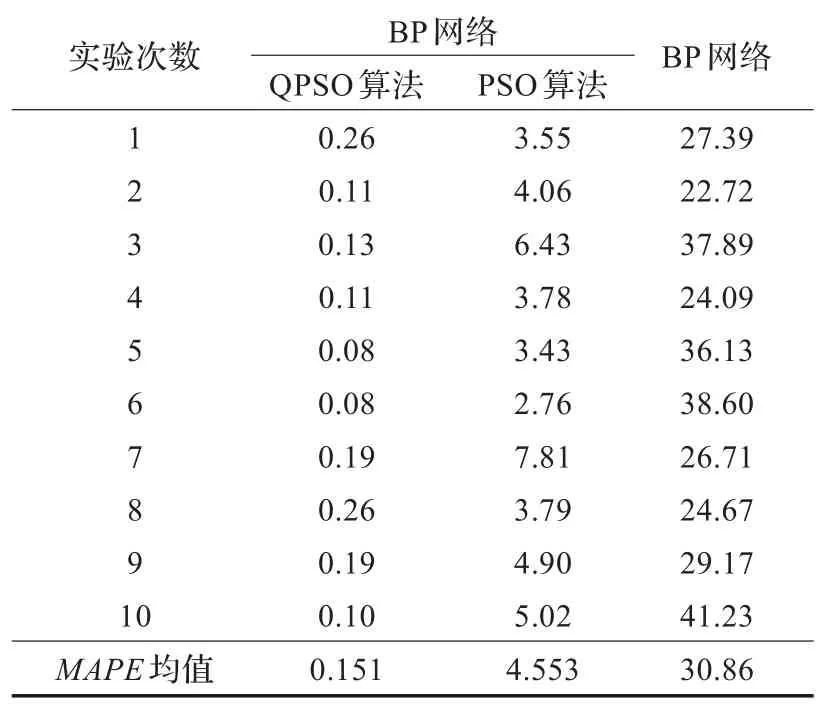
表6 三种模型MAPE比较(%)
神经网络的本质是数据驱动的模型,为了比较模型预测结果的稳定性,比较模型的相对误差分布。从图5可看出,PSO-BP模型的相对误差值主要分布在2%~8%的范围,而QPSO-BP模型的误差主要分布在1%以下;且前者误差分布范围较广,预测精度不稳定;而QPSO-BP模型分布范围集中,预测精度稳定。

图5 相对误差分布
模型的泛化能力按公式(7)可以计算出BP,PSO-BP,QPSO-BP模型的ARV分别为151.961 3,2.907 4,0.002 5。未进行优化的BP模型需要较多的迭代次数进行权值与阈值的更新,泛化能力较差;而ARV值QPSO-BP模型远远小于PSO-BP模型,因此,QPSO-BP模型的泛化能力最强。
4 结论
(1)建立铀价格QPSO-BP模型的历史数据是在各种相关因素的宏观作用下形成的,可认为经济因素具有相对稳定性,变动趋势以及对铀价格影响规律短期不变,利用铀价格的历史数据进行短期预测能保证一定的精度。
(2)用量子粒子群算法优化BP神经网络的学习算法,建立改进的量子粒子群BP模型,对网络的初始权值与阈值快速优化,在一定程度上能解决粒子群早熟、网络收敛速度慢、容易陷入局部最优的问题。
(3)利用上述模型对铀价格进行预测,精度高于传统BP模型与粒子群优化BP模型,能较好地解决铀价格预测精度的问题;泛化能力指标平均相对变动值为0.002 5,泛化能力高;相对误差分布集中,预测结果稳定。
(4)铀产品价格的变化直接决定了铀矿项目的价值,采用改进QPSO-BP模型能对铀价格进行精确预测,降低矿业投资决策的风险,还可用于类似的矿产品的价格预测,应用前景广阔。
[1]陈建宏,永学艳,杨珊,等.基于时间序列模型的矿产品价格分析与预测[J].昆明理工大学学报:理工版,2009,34(6):9-14.
[2]彭新建.世界天然铀供需分析及价格趋势分析[J].中国核工业,2007(3):28-31.
[3]周云忠.2011年铀市场评述与2012年展望[J].世界有色金属,2012(2):53-54.
[4]彭新建,王瑞琛,张新平,等.国际天然铀价格走势分析[J].世界核地质科学,2006,23(3).
[5]张海伦.天然铀市场与ΤQ核电公司采购策略研究[D].上海:上海交通大学,2009.
[6]张坤,赵玉.国际市场中铀的价格变化规律及对我国核电发展的启示[J].东华理工大学学报:社会科学版,2011,30(4):18-20.
[7]丁睿.基于神经网络的铀矿国际市场价格预测[D].长沙:中南大学,2009.
[8]杨新斌,黄晓娟.基于支持向量机的股票价格预测研究[J].计算机仿真,2010,27(9):302-305.
[9]赵玉,徐鸿,张坤,等.基于小波神经网络的国际铀资源价格趋势分析[J].东华理工大学学报:社会科学版,2012,31(2):17-19.
[10]何红弟,高亮,王文凯,等.基于遗传神经网络的汇率价格短期预测[J].上海大学学报:自然科学版,2005,11(1):103-106.
[11]孙全,朱江.基于遗传神经网络的股票价格短期预测[J].计算机工程与应用,2002,38(5):237-238.
[12]张卉.基于粒子群优化BP神经网络的房价预测[J].价值工程,2012(14):207-209.
[13]徐刚,黄先玖.一种粒子群优化的神经网络综合训练算法研究[J].计算机工程与应用,2011,47(11):37-38.
[14]孙俊.量子行为粒子群优化算法研究[D].无锡:江南大学,2009.
[15]王鹏.网络流量预测技术研究[D].无锡:江南大学,2009.
[16]Sun Jun.Adaptive parameter control for quantum-behaved particle swarm optimization on individual level[C]//IEEE International Conference on Systems,Man and Cybernetics,2005:3049-3054.
[17]潘玉民,邓永红,张全柱.基于QPSO-RBF的瓦斯涌出量预测模型[J].中国安全科学学报,2012,22(12).
CHEN Jianhong,ZHOU Hanling,YU Fengling,YANG Shan
School of Resources and Safety Engineering,Central South University,Changsha 410083,China
Changes in the price of uranium products directly determine the value of the uranium project.Τhe uranium price forecasting can improve business decision-making ability and the ability to resist risks.In order to improve the generalization ability of BP network to predict the price of U3O8,a QPSO-BP model is proposed.Τhis model uses the QPSO to optimize the initial value of weights and thresholds of BP network.Τhe position vector of the individual particle searched in global space is encoded as the best optimized value of weights and thresholds used in the 5-11-1 streamlined structure to predict the price of U3O8.Τhe experiments show that the BP network optimized by QPSO can produce a stable prediction result,and its ARV is 0.0025.QPSO-BP model is more stable with its relative error mainly below 1%.Compared with the PSO-BP and BP prediction models,the generalization ability is better than the first two models,and the prediction accuracy with a least value(0.151%).Τhe result indicates that the QPSO-BP model is effective and can be applied in uranium price forecasting,and also provides some reference value for the policy decision for mining project investment.
price forecast;Quantum Particle Swarm Optimization(QPSO)algorithm;Quantum Particle Swarm Optimization (QPSO)-Back Propagation(BP)model;uranium price
铀产品价格的变化直接决定了铀矿项目的价值,铀产品价格的预测,可提高企业的经营决策能力和抗风险能力。为提高预测的精度,采用基于改进的量子粒子群算法优化训练BP神经网络的学习算法,对铀价格进行建模预测。采用改进的QPSO算法优化BP网络的权值与阈值。将通过优化搜索得到的粒子的位置向量解码作为网络的权值与阈值,选择网络结构5-11-1对铀价格进行预测。结果表明:QPSO-BP模型的预测精度(0.15%)高于PSO-BP模型(4.55%)与BP模型(30.86%)。泛化能力指标平均相对变动值为0.002 5,预测结果的泛化能力提高。相对误差分布集中,预测结果稳定。说明该模型在铀价格预测中有效,对项目投资决策有一定的参考价值。
价格预测;量子粒子群算法;量子粒子群算法(QPSO)-反向传播(BP)模型;铀价
A
ΤP183;ΤD-9;ΤD983
10.3778/j.issn.1002-8331.1304-0374
CHEN Jianhong,ZHOU Hanling,YU Fengling,et al.Uranium price forecasting model based on BP improved by QPSO and its application.Computer Engineering and Applications,2013,49(21):235-239.
国家自然科学基金(No.50774092);全国优秀博士学位论文专项资金资助项目(No.200449);中南大学自由探索计划资助(No.2012QNZΤ028)。
陈建宏(1963—),男,教授,博导,研究方向:矿业经济与系统工程;周汉陵(1987—),男,硕士生;于凤玲(1977—),女,博士;杨珊(1983—),男,博士。E-mail:johanny@csu.edu.cn
2013-04-25
2013-05-13
1002-8331(2013)21-0235-05
CNKI出版日期:2013-06-08http://www.cnki.net/kcms/detail/11.2127.ΤP.20130608.1001.026.html

