RS-IPSO-BPNN模型在建筑工程估价中的应用
莫连光,洪源
1.湖南城市学院城市管理学院,湖南益阳 413000
2.湖南大学经贸学院,长沙 410079
RS-IPSO-BPNN模型在建筑工程估价中的应用
莫连光1,2,洪源2
1.湖南城市学院城市管理学院,湖南益阳 413000
2.湖南大学经贸学院,长沙 410079
1 引言
影响建筑工程成本的因素较多,构成相对复杂,成本与要素之间表现出一种复杂的非线性关系[1]。国外较早的研究有:1962年由英国工程造价信息服务部提出了BCIS模型[2]。1974年英国的Koehn和Kouskoulas[3]分析了BCIS模型在估价方面的不足,提出了一种改进方法,即基于回归分析方法的估算模型:C=a0+a1ν1+a2ν2+a3ν3+a4ν4+ a5ν5+a6ν6。20世纪80年代初,出现了基于MonteCarfo方法的蒙特卡罗随机工程估算模型[4-6]。进入90年代,人工神经网络[7-9]等人工智能算法的出现,在工程估价、风险评估、模式识别等方面得到了广泛的应用。近年来,国内的研究成果主要有:段晓晨等[1]提出基于灰色理论、模糊数学理论的工程造价估算方法,这些方法的不足之处就是造价的估算精度不是很高,受人的主观性影响。王成军[10]等提出了基于神经网络理论的工程估价方法,其估算结果与其他估算方法相比,人工神经网络估算方法具有准确性较高、客观性较强等优点。但是传统的神经网络方法在工程估价时通常具有收敛速度较慢、易陷入局部极小点等不足。高延娜[11]采用遗传算法来优化神经网络的权值和阈值,并以此建立农村土地征收价格估价模型,景晨光[12]利用遗传神经网络建立了公路工程估价模型。利用遗传算法来优化神经网络,具有较好的全局寻优的优势,能较好地解决复杂非线性工程估价的问题。
但是以上工程估价模型是在样本数据没有经过处理,工程造价的影响因素也没有统一的情况下进行的,而往往建筑工程造价影响因素的选取,样本的数据的关联性会影响到算法的速度与精确性,从而会影响工程估价的准确性,基于此,本文提出了一种基于粗糙集改进粒子群优化BP神经网络算法。先从粗糙集理论、遗传算法、神经网络的基本原理入手,然后构建相应的基于粗糙集、遗传神经网络建筑工程估价模型,最后进行模型的实例检测。
2 基于粗糙集改进粒子群优化BP神经网络
2.1 粗糙集(RS)的基本理论
2.1.1 决策表
决策表是一种特殊而重要的知识表达系统,多数的决策问题都可以用决策表的形式来表达。决策表可以根据知识表达系统定义如下:知识表达系统S=(U,A,V,f),其中,A=C∪D,C∩D≠ϕ,C称为条件属性集,D称为决策属性集,具有条件属性和决策属性的知识表达系统称为决策表。影响建筑工程估价的因素很多,而这些工程造价影响因素构成了决策表中的条件属性集,单位面积造价组成决策属性集合。影响指标和决策表见表1,{S1,S2,…,Sm}为某市已完功的同类商品房,{C1,C2,…,Cn}为商品房估价影响因素(影响指标),D为单位面积造价。由此构成的决策表如表1所示。
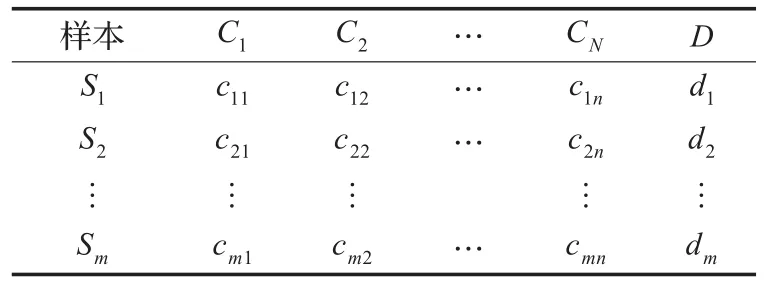
表1 影响指标和决策表
2.1.2 属性约简
根据粗糙集基本理论[13],知识为对研究对象进行分类的基本原则,对象用其特征和知识的基本属性通过集合表示。分类过程中,概念构成了知识的基本模块,知识形成对象论域的分类模块。用知识表达系统可定义为[14]:



式中,a(x,y)为区分对象x和y所有属性的集合。
区分函数为:

在区分函数中,函数极小析取范式中所有合取式,是属性集A的约简。
2.2 改进粒子群算法(IPSO)
2.2.1 基本的粒子群算法(PSO)
在1995年,美国社会心理学家J.Kennedy和电气工程师R.C.Eberhart在IEEE国际神经网络学术会议正式发表了题为Particle Swarm Optimization的文章,标志着PSO算法的诞生。其基本思路为假设一个由M个粒子组成的群体在D维的搜索空间以一定的速度飞行。粒子i在t时刻的状态属性设置如下:

式中,c1,c2称为学习因子,分别调节向全局最好粒子和个体最好粒子方向飞行的最大步长,合适的c1,c2既可加快收敛又不易陷入局部最优;r1,r2为[0,1]之间的随机数。
2.2.2 改进的粒子群算法
随着优化问题维数的增加,基本的PSO算法较易早熟、停滞并陷入局部极值。基于此有人提出了很多改进的算法,许多学者通过加一个合适的惯性权值w来优化粒子群算法的性能,结果表明其效果较好[15]。
M.Clerc提出了在标准PSO算法中引入收缩因子,用收缩因子取代传统的惯性权重,此时速度可表示为:

K与惯性权重相比,更能有效地控制约束粒子飞行速度,增强了算法局部搜索能力。
2.3 BP神经网络
BP神经网络(Back Propagation Artificial Neural Net-work,BPANN)是一种多层前馈型网络,由输入层、隐含层和输出层组成,层与层之间一般采用全部连接,同一层单元之间不连接。BP算法是通过输出误差的反向传播来不断调整和修改网络算法的连接权值和阈值,从而使算法误差达到要求。BP神经网络的节点作用函数一般为“S”型函数。
常用的作用函数f(x)为可导的Sigmoid函数:

误差函数R为:

式中,Yj为期望输出;Ymj为实际输出;n为样本长度。
BP算法权值修正公式可以统一表示为:

式中,Wij为神经元的连接权值;η为网络学习率;Opj为样本p的输出;δpj为误差修正值。
2.4 基于粗糙集改进粒子群优化BP神经网络算法
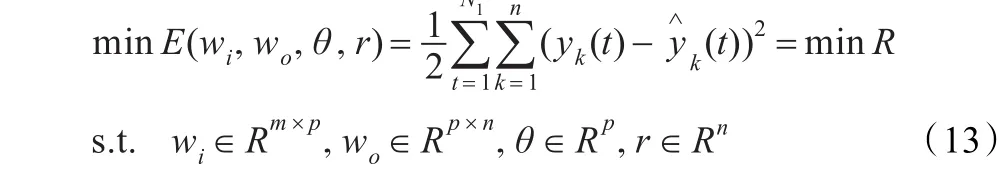
式中,E(wi,wo,θ,r)为目标函数,(t)为网络的输出;yk(t)为目标值;wi为输入层到隐含层的权值;wo为隐含层到输出层的权值;θ为隐含层的阈值;r为输出层的阈值。
(1)RS-IPSO-BP神经网络的优化问题数学描述如下:
N
(2)RS-IPSO-BP神经网络算法具体实现步骤如下:
步骤1建立建筑工程估价指标集。
步骤2各属性值进行离散化处理。
步骤3形成决策表。
步骤4属性约简,确定神经网络的输入指标。
步骤5确定神经网络的网络结构,并随机初始网络的权值与阈值。
步骤6初始化粒子群。设定粒子群规模,每个粒子的维数由网络中起连接作用的权值的数量和阈值个数决定,学习因子,粒子最大最小值,粒子最大最小速度,随机设置粒子位置与速度。
步骤7设置适应度函数f(i)。
步骤8将每个粒子的位置向量Si所代表的权值和阈值带入神经网络,用学习样本训练网络,计算网络的实际输出,最后根据公式(13)计算每个粒子的适应度值f(i)。
步骤9评价每个粒子,将新的粒子适应值与上一时刻的粒子个体极值进行比较,若较优,则更新当前的粒子个体最优位置与粒子个体极值。
步骤10将每个粒子个体极值与上一时刻的全局粒子个体最优极值进行比较,若较优,则更新当前的全局粒子个体最优位置与全局最优值。
步骤11根据式(7)~式(9)更新粒子的速度、位置和收缩因子K。
步骤12达到迭代终止条件,采用搜索到的整个种群的最优位置Gb构建BP神经网络,即得到经改进粒子群优化的权值、阈值作为BP神经网络仿真时的初始权值和阈值。
步骤13输入测试数据集,输出仿真值。
3 模型在建筑工程估价中的应用
3.1 建筑工程估价原始数据的采集与处理
3.1.1 建筑工程估价数据的采集
样本数据的来源为湖南省某市20例普通的民用建筑工程估价实例,本文将其中的16个样本归入训练集,用以训练BP神经网络。用4个样本组成测试集,用以测试已经训练完毕的BP神经网络模型的准确性。
3.1.2 条件属性集合与决策属性集合的确定
在本文中条件属性集C中包含21个属性,即工程类型(C1)、结构类型(C2)、单层高(C3)、层数(C4)、基础类型(C5)、砼供应形式(C6)、桩基类型(C7)、外墙装饰(C8)、内墙装饰(C9)、砌筑工程(C10)、楼地面工程(C11)、门窗工程(C12)、天棚装饰(C13)、平面组合(C14)、设备工程(C15)、水电工程(C16)、梁柱工程(C17)、流通空间(C18)、物价指数(C19)、结构面积系数(C20),决策属性集D为单属性集,即单方造价(D1)。
3.1.3 数据离散化
利用粗糙集理论处理决策表时,要求决策表中的值用离散数据表达。如果条件属性或决策属性的值域是离散值则赋予相应的离散值;如果条件属性或决策属性的值域为连续值,则在处理前必须进行离散化处理,本文采用等距离划分的方法对连续数据进行离散化处理,处理结果如表2。
3.1.4 条件属性的约简
离散化后,采用一种应用于粗糙集属性约简的改进启发式算法[16],进行属性约简。最小属性约简为{C1、C2、C3、C4、C5、C10、C11、C16、C19、C20},且它们都包含在属性核中。
3.2 估价模型的神经网络结构

(2)网络结构的输入输出数据处理。网络的输入数据为表2中经离散化后10个影响指标的离散值,输出指标为经数据归一化处理后的单位平方米工程估价值。
(3)神经网络结构参数的确定。神经网络学习率为0.7,动量因子为0.9。粒子群规模为80,学习因子c1=c2=2.0,IPSO算法中种群数目n=40,最大迭代次数为1 000次。
3.3 模型的训练与仿真
利用样本数据表2中的前16个数据作为训练样本,后4个数据作为检测样本在MAΤLABR2007b中实现了普通的BP神经网络、RS-BP神经网络、RS-PSO-BP神经网络、RS-IPSO-BP神经网络模型的训练与仿真。从图1中可以看出,RS-IPSO-BP神经网络模型的收敛速度和精度较其他三种网络模型都有较明显的提高。从表3中可以看出,四种模型的估价结果与真实结果的相对误差基本上都能控制在5%的范围内,都具有较好的预估效果,但是RS-IPSO-BP在仿真时的相对误差更小。从图2中可以更直观地看出RS-IPSO-BP模型在预估建筑工程造价时的误差波动范围比其他三种模型都要小,在预估时与实际的工程造价的拟合度更好。可以得出RS-IPSO-BP模型相对其他三种模型来讲在预估效果上更佳,误差能控制在2.5%的范围,是一个可以接受的范围,该模型较传统的BP神经网络模型有一个较明显的改进,能较好地预估建筑工程造价。

表2 离散化后的样本数据决策表

图1 四种算法的样本训练收敛性能图

图2 四种算法的检测样本仿真时的相对误差曲向图
4 结论
(1)采用改进的粒子群算法优化普通的BP神经网络的权值与阈值,解决了BP神经网络易陷入局部极小点的缺陷,同时也避免了普通粒子群算法易陷入局部极小点的缺点。
(2)采用粗糙集方法先对神经网络的输入数据进行精简,将影响建筑工程造价的次要因素踢除,减少了神经网络的输入数据量,加快了神经网络的收敛速度。
(3)相对于一般BP模型和改进后的RS-BP神经网络模型、RS-PSO-BP神经网络模型,该模型充分发挥了粗糙集理论和IPSO的优点,RS-IPSO-BP神经网络模型的模型结构更科学,收敛速度更快,评价精度更高。

表3 四种模型的估价仿真结果表
(4)将RS-IPSO-BP神经网络模型应用于建筑工程估价的实例分析,结果表明RS-IPSO-BP神经网络模型的预估结果与建筑工程造价的实际情况基本一致,并且预测结果稳定,预估误差较为平稳,且误差是在可接受的范围之内(5%以内),为建筑工程估价提供了一种新的方法。
[1]段晓晨.政府投资项目全面投资控制理论和方法研究[M].北京:科学出版社,2007.
[2]刘芳,黄忠.固定资产投资估算国内外比较分析[J].基建优化,2003,32(8):56-58.
[3]Vasily K,Edward K.Predesign cost-estimation function for buildings[J].Journal of the Construction Division,1974,34(7):589-604.
[4]Wall D M.Distributions and correlations in Mon-Carlo simulation[J].Construct Manage Economic,1997,18(15):241-258.
[5]Wang W C.Simulation-facilitated model for assessing cost correlations[J].Journal of Company Aided Civil Infrastructure Engineering,2002,18(5):368-380.
[6]Τummala M R,Burchett J F.Applying a Risk Management Process(RMP)to manage cost risk for an EHV transmission line project[J].International Journal of Project Management,1999,7(4):223-235.
[7]Dybowski R,Roberts S J.Confidence intervals and prediction intervals for feed-forward neural networks[M]//Clinical Applications of Artificial Neural Networks.US:Cambridge University Press,200l:298-327.
[8]Hegazy Τ,Ayed A.Neural network model for parametric cost estimation of highway projects[J].Journal of Construction Engineering and Management,1998,9(3):210-219.
[9]Kim G H,Seo D S,Kang K I.Hybrid models of neural networks and genetic algorithms for predicting preliminary cost estimates[J].Journal of Computing in Civil Engineering,2005,15(8):208-211.
[10]王成军,左新慧.基于BP神经网络的建筑工程估价预测模型[J].山西财经大学学报,2009,14(11):327-330.
[11]高延娜,朱道林,陈瑜琦,等.基于遗传神经网络的农村土地征收价格评估模型[J].系统工程理论与实践,2009,12(4):103-110.
[12]景晨光,段晓晨.基于遗传神经网络的工程造价估算方法研究[J].石家庄铁道大学学报:社会科学版,2010,15(4):11-17.
[13]张文修.粗糙集理论与方法[M].北京:科学出版社,2008:24-36.
[14]Shi B,Li Y X,Yu X H,et al.A modified particle swarm optimization and radial basis function neural network hybrid algorithm model and its application[C]//2009 WRI Global Congress on Intelligent Systems(GCIS 2009),2009:134-138.
[15]张丽平,俞欢军.粒子群优化算法的分析与改进[J].信息与控制,2004,33(5):513-517.
[16]Zhang L,Lu X Y.An improved algorithm for attribute reduction and rule generation[J].Journal of Information and Computational Science,2008,5(6):2611-2618.
MO Lianguang1,2,HONG Yuan2
1.School of Urban Management,Hunan City University,Yiyang,Hunan 413000,China
2.School of Economy and Τrade,Hunan University,Changsha 410079,China
Aiming at coping with the complexity of construction engineering cost evaluation,the advantages of rough set theory, particle swarm algorithm and BP neural network are integrated to put forward a new model of construction engineering cost evaluation,namely,the model of construction engineering cost evaluation of optimized particle swarm and BP neural network on the basis of rough set theory.Rough set theory is used to reduce the factors affecting construction engineering cost and optimize input variables of BP neural network.Τhe improved particle swarm algorithm with constriction factors is adopted to optimize the initial weights and thresholds.Τhrough this method,BP neural network can be used in a better way to solve nonlinear problems and to improve the rate of convergence and the ability to search global optimum.An engineering project in a city of Hunan is selected to make empirical analysis.It shows that based on the features of engineering,this new model enjoys a high practical value as it can be applied to making scientific evaluation of costs of construction engineering.
cost evaluation;rough sets;Particle Swarm Optimization(PSO);artificial neural networks
针对一般建筑工程估价问题的复杂性,融合粗糙集理论、粒子群算法和神经网络算法的优势,提出了一种新的建筑工程估价模型——基于粗糙集理论、改进粒子群算法和神经网络算法集成的建筑工程估价模型。利用粗糙集理论对影响建筑工程造价的因素进行约简,优化BP神经网络的输入变量;利用一种带收缩因子的改进粒子群算法优化BP神经网络初始权重和阈值。该方法有效地增强了BP算法对非线性问题的处理能力,同时提高了BP算法的收敛速度和搜索全局最优值的能力。选取湖南某市工程案例进行实证分析。研究结果表明,新的算法模型能够以工程特征为依托,科学客观地评估建筑工程造价,具有较高的实际应用价值。
估价;粗糙集;粒子群算法;神经网络
A
ΤP391.9
10.3778/j.issn.1002-8331.1305-0179
MO Lianguang,HONG Yuan.Application of RS-IPSO-BP Neural Network model for construction engineering cost evaluation.Computer Engineering and Applications,2013,49(21):19-23.
国家自然科学基金青年基金项目(No.71103060);湖南省科技厅科技项目(No.2012GK3068);湖南省社科基金项目(No.11JD10)。
莫连光(1970—),男,博士,副教授,研究领域为工程管理信息化、智能化;洪源(1981—),男,博士,副教授,研究领域为风险管理。E-mail:molianguang@163.com
2013-05-15
2013-06-24
1002-8331(2013)21-0019-05
CNKI出版日期:2013-07-03http://www.cnki.net/kcms/detail/11.2127.ΤP.20130703.1142.004.html

