基于LIBSVM和时间序列的区域货运量预测研究
曾鸣,林磊,程文明
1.西南交通大学机械工程学院,成都 610031
2.纽约州立大学布法罗分校土木工程学院,美国布法罗 14260
基于LIBSVM和时间序列的区域货运量预测研究
曾鸣1,林磊2,程文明1
1.西南交通大学机械工程学院,成都 610031
2.纽约州立大学布法罗分校土木工程学院,美国布法罗 14260
1 引言
区域货运量是反映地区运输需求的一项重要指标,同时也是进行地区运输系统规划和管理的基础,其预测精度和误差水平对整个区域的运输组织、规划、管理和决策等都会产生十分重要的影响。因此,选择一种精度较高的预测方法,对区域未来的货运量进行分析研究具有较强的理论和实际意义。区域货运量产生的影响因素众多,不仅包括该地区的运输系统供给,而且涵盖大量的区域经济因素,同时各影响因素对整个区域货运量的影响程度也不尽相同,使得区域货运量预测问题具有模糊性和高度非线性的特点。此外,由于人力、物力以及技术等方面的限制,统计过程常受到各种噪声干扰,一些区域的统计资料尚不完备,无法获得足够多的样本,使得预测精度无法保证。
由此可见,区域货运量预测的关键在于解决高维度非线性小样本预测问题。传统的货运量预测方法包括回归分析法[1]、时间序列分析法[2]、因果分析法、弹性系数法,以及综合这些方法的组合预测方法[3]等,然而这些方法所建立的模型大都不能准确反映数据复杂的内部结构,造成信息量丢失和结果失真。当前货运量预测大多采用模糊[4]、小波分析[5]、灰色模型[6-7]以及神经网络[8-9]及其相应的改进,如BP[10]、RBF[11]、广义回归神经网络以及这些方法的组合[12]。虽然这些方法能够较好地解释数据非线性关系,但对于区域货运量这类影响因素多、样本量较小的预测问题仍具有很大局限性,不能保证其预测精度。为此,本文提出了将MI与LIBSVM支持向量回归模型以及状态空间时间序列模型相结合的预测方法,采用互信息(Mutual Information,MI)方法在不减少货运量影响因素信息量条件下,进行综合信息提取和降维,以解决信息冗余、噪声和维数过高的问题。将所得低维空间作为输入,并在此基础上分别建立(Library for Support Vector Machines,LIBSVM)支持向量回归预测模型以及状态空间时间序列预测模型。通过重庆市货运量预测算例分析,验证了方法的有效性。
2 综合信息提取及数据降维
高维度特征降维方法主要分为特征抽取和特征选择两种类型。相对于主成分分析、非线性PCA网络、独立成分分析等特征抽取方法涉及语义分析,特征选择方法选出的特征集是原始特征集的子集,组成的新低维空间不改变原始特征空间的性质,因此更容易实现且效果更为显著。本文采用典型的特征选择方法互信息MI[13]对原始特征空间进行降维。作为高维数据的分离度量方法,MI建立了高维特征提取向量与输出分类信息之间的内在联系,是一种有效的信息判据特征提取方法。
根据信息论[14],熵用以度量随机变量的不确定性,因此信息类别ω=() ω1,ω2,…,ωn的熵可以表示为:

信息类别与特征向量F=() f1,f2,…,fn的联合熵为:
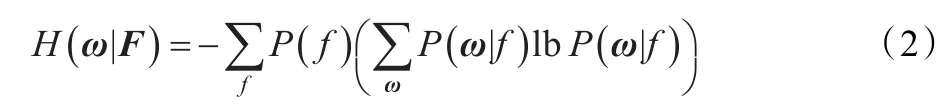
根据定义,信息类别ω与特征向量F之间的互信息可由以下公式计算:
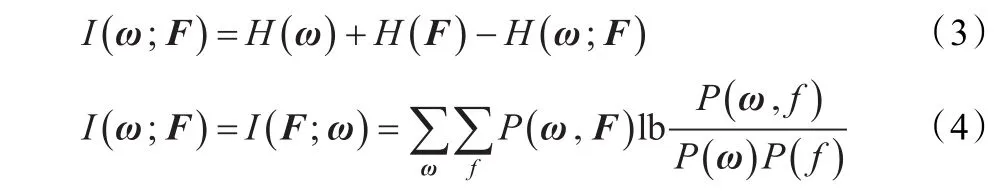
其中P(ω,f)为联合概率密度,P(ω) P(f)为边缘概率密度。互信息值越大,表示变量间的相关度越高。
对于区域货运量而言,当其受到如政策变化、自然灾害等一些特殊原因影响时,该区域货运量在所对应的预测单位时间内,会产生剧烈增加或者减少。经分析,这种影响的本质,仍由这些特殊原因引起的货运量相关影响因素大幅变动所体现,并且这些影响因素对于最终预测结果通常具有更为直接的影响。因此,为综合考虑此类区域货运量预测问题,同时反映上述特点,决定引入判别因子σi及调整系数λi。

其中fti表示第t个单位时间内第i个特征的值。调整系数:

其中Q(σi)表示满足σi〉0的判别因子数量。
通过判别因子及调整系数的计算,使发生剧烈变化且具有较大互信息值的影响因素,首选进入新的特征集合,并以此首选特征为基础,计算确定其他选择特征,从而提高预测结果的准确度。
以MIFS算法[15]为基础,具体步骤如下:
第一步,初始化特征集合F,使其含有N个特征,设置集合A为空集。
第二步,计算判别因子σi,i=1,2,…,N及Q(σi)。当Q(σi)〉0,σi〉0,令相应调整系数λi=1;当Q(σi)〉0,σi≤0,令相应调整系数λi=0;当Q(σi)=0,则令所有调整系数λi=1。
第三步,计算特征集合F中的每一个特征fi,i=1,2,…, N与信息类别ω之间含有调整系数的互信息λiΙ() ω;fi,i= 1,2,…,N。
第四步,找出使λiΙ(ω;fi)最大的首选特征fm,将其赋给集合A的同时从原特征集合F中消除。

原特征集合F中消除;若不成立,则令λi=1,i=1,2,…,N-1然后进行上述特征选择。重复以上贪心选择方法直到找出所有k个特征,即|| A=k。第六步,输出含有全部所选择特征的集合A。
3 预测模型
支持向量回归(Support Vector Regression,SVR)是Vapnik[16]在1995年基于统计学习理论提出的一种机器学习方法,它涵盖了支持向量机(SVM)的许多优点,在许多领域得到广泛应用。支持向量机体现了结构风险最小化以及泛化误差上界最小化的原则,其最初产生的目的是为了解决分类问题。在1997年Vapnik提出不敏感损失函数后,支持向量机方法的应用领域得以延伸,形成了支持向量回归方法(SVR)用以解决非线性回归问题[17]。
状态空间时间序列模型与其他时间序列方法不同,它以模型结构和组成成分分析为基础,当模型结构随着时间发生变化时,具有很强的灵活性。同时,该模型能够很好地处理观测值丢失的问题,并且通过将卡尔曼滤波引入最终的预测,能够更直接地获得所需的估计值及标准差。
3.1 LIBSVM支持向量回归模型
支持向量回归方法为:给定数据点集{(x1,y1),(x2,y2),…,(xn,yn)}⊂X×R,其中X表示输入模式空间,n表示总的训练样本个数。根据数据点集可建立以下线性回归方程:f(x)=〈ω,x〉+b,ω∈X,b∈R,〈,〉表示X中的点积,b表示标量阈值。假设一个不敏感损失函数ε,允许计算值与实际值之间存在一定范围或区间内的可忽略误差,ω和b可由下式进行计算:同时满足约束:

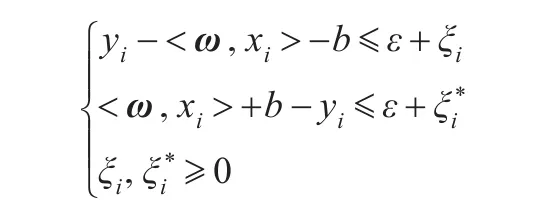
其中,ε(≥0)为不敏感损失函数,表示允许的最大误差。C(≥0)为训练过程中与超出误差相关的惩罚。ξi,ξ*i为松弛变量,表示超出允许误差的程度。二者分别对应计算值小于实际值,以及计算值大于实际值的两种情况。
为解决以上最优化问题,支持向量回归首先通过非线性映射将训练样本映射到高维内核诱导特征空间,其次在该空间内进行线性回归。若用φ() X表示从输入空间到高维特征空间的非线性变换,那么特征空间分类超平面可以表示为:

上式中,φ(Xj)表示第j个输入模式Xj经非线性映射,在高维特征空间中的像,φ(X)表示输入向量X在高维特征空间中的像。可见内核映射是仅由输入数据向量的点积所决定隐式,因此能够保证在较低的计算复杂度基础上,将数据映射到非常高的维度。内积核函数不同算法不同,径向基函数(RBF)K(x,y)=exp(-γ|x-y|2)就是一种常见的核函数。支持向量回归的参数,即核函数中的γ以及惩罚因子C则通过折交叉验证法[18]进行优化计算。
3.2 状态空间时间序列模型
状态空间时间序列模型对于区域货运量预测同样具有很强的针对性。其中,状态由包含所有信息的向量组成,同时这些信息在将来会继续存在。即,状态向量是过去的一系列线性无关信息的线性组合,这些信息同时又与将来的内生变量有关。通过连续预测,可以得到相应的状态向量。时间序列的多元状态空间模型为:

第一个等式为观测方程,第二个等式为状态方程。其中,Yt表示t时刻非观测数据向量,即预测单位时间内的货运量。Xt是一个p维向量,表示在t时刻状态的观测值,其变化过程由状态方程控制。这里用以表示与区域货运量相关的各影响因素。Dt表示对Xt进行的与时间顺序有关的线性变换。Zt表示由外生回归量所组成的K维向量,这里表示政策、自然因素等外生变量。E表示对K维向量Zt的回归。Vt为观测噪声。{Nt,t=1,2,…,n}序列由独立同分布的p维随机向量组成。其中,前s个元素的非奇异协方差矩阵为A,均值为0;后p-s个元素全部为0。{Vt,t=1,2,…,n}序列由独立同分布的r维随机向量组成。其中,前m个元素的非奇异协方差矩阵为B,均值为0;后r-m个元素全部为0。初始状态X0用以计算μ的均值以及非奇异协方差矩阵Σ。
对于所有的t和t′,Vt与Nt相互独立,Vt,Nt与X0之间相互独立。假设随机向量X0,Vt,Nt服从多元正态分布,给定X0,X1,…,Xn,Y1,Y2,…,Yn,Z1,Z2,…,Zn为常数值,则有对数似然函数:

通过状态空间求解过程,即使得lbL最大化,从而得到参数φ,E,A,B的值。
4 重庆市货运量预测分析
搜集重庆市2000年至2010年的人口数量、运输线路长度(含铁路营业里程、内河航道里程以及公路里程)、国内生产总值、全社会固定资产投资、工业总产值、财政收入等36项与货运量产生密切相关的指标作为原始数据输入,以该区域年度货运量(数据均依照我国货运量统计标准,铁路按货物发送量统计,公路按货物到达量统计,内河运输按发送量,近海运输按到达量统计)为输出,具体样本值见表1。由于样本数据维数高且不满足一般传统预测方法对样本数量的要求,因此采用本文所提出的方法,在原始数据互信息特征降维基础上,分别使用LIBSVM支持向量回归以及状态空间时间序列模型进行货运量预测。
为消除原始数据在数量级及量纲的不同,经数据归一化处理后,按照第1章互信息特征降维原理及算法编写程序,计算各影响因素之间的互信息值Ix为:

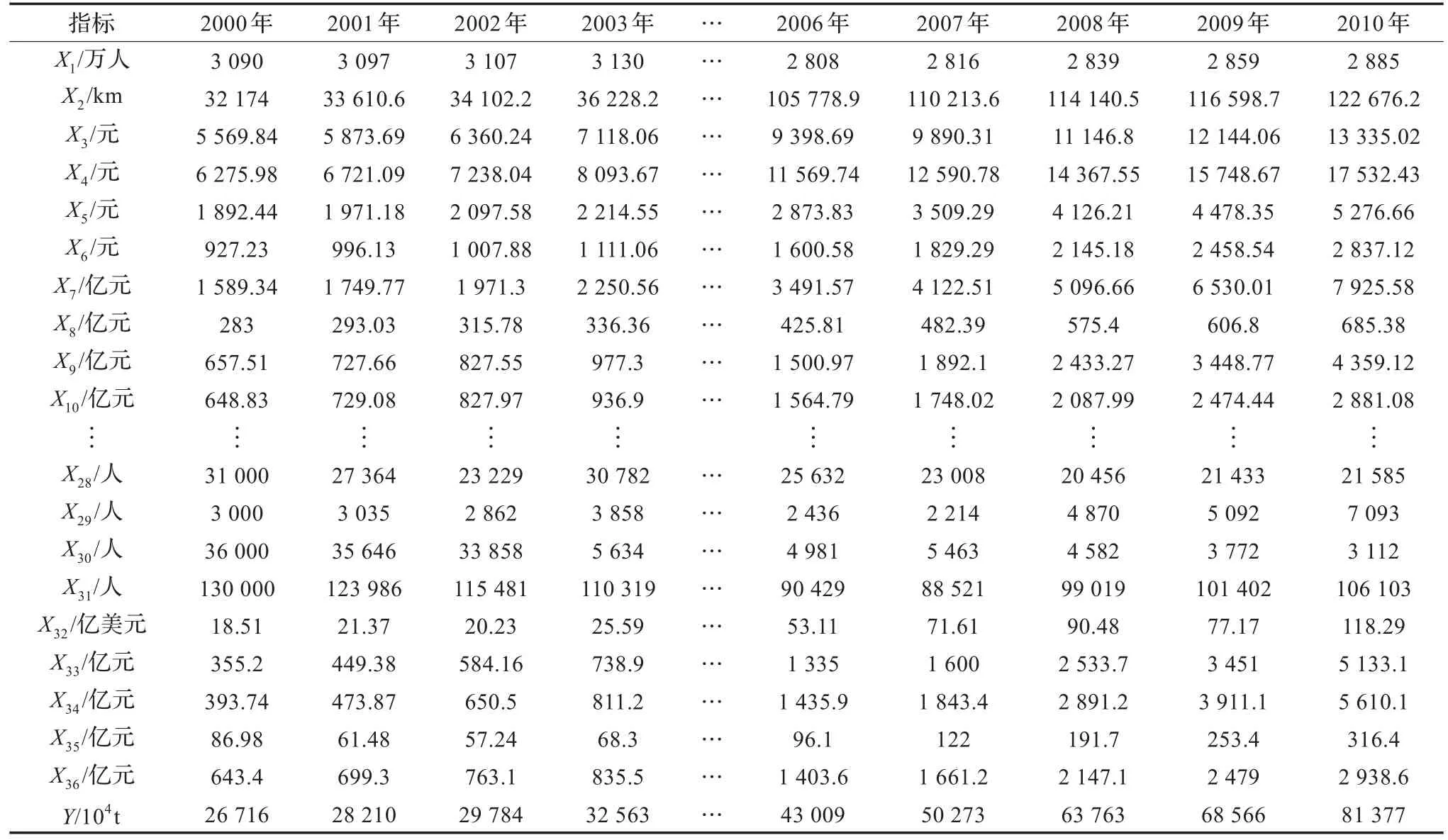
表1 重庆市货运量预测样本数据
同理计算各影响因素与输出变量之间的互信息值Ix,y为:

根据前面区域货运量预测模型及算法,采用R-2.15.1编写状态空间时间序列模型计算程序,以2000年各影响因素指标数据作为初始状态X0,2000年至2007年各指标数据作为学习样本进行训练,令时间t=0,1,…,7。同时,采用Matlab2011编写LIBSVM支持向量回归模型计算程序,将(RBF)径向基函数作为该模型内积核函数,设置不敏感损失函数ε为0.01。以2000年至2007年各指标历史数据作为学习样本输入,则有输入数据X(t)=[X(1),X(2),…,X(8)]Τ,区域货运量实际值Y(t)=[y1,y2,…,y8]Τ。训练过程采用动态更新方式进行,即模型总是利用当前最新的训练结果,预测下一阶段的值。惩罚因子C以及核函数参数γ在样本训练过程中采取调优方式取值。

图1 未采用互信息降维的各模型预测结果
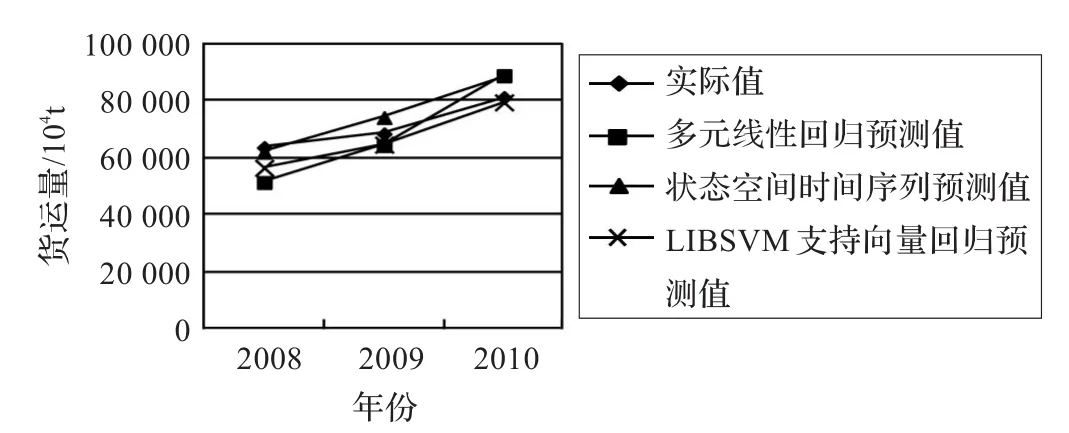
图2 采用互信息降维的各模型预测结果
将以上经过训练的模型,应用于重庆市2008年至2010年货运量预测。同时,为检验互信息降维方法对模型预测结果的影响,以模型的输入数据是否采用互信息降维为标准,对几种模型前后预测效果进行对比实验,实验结果如图1、图2所示。使用Minitab16进行多元线性回归预测,各种预测方法最终结果及相对误差见表2。通过重庆市货运量预测实验结果可以得出以下结论:(1)采用互信息高维度特征降维方法,在不改变原始特征空间性质的基础上,选出原始特征集的子集,形成新的低维空间,有效地解决了原始数据存在的冗余、噪声以及相关性问题。因此,在互信息特征降维基础上建立起来的预测模型和算法,预测精度普遍高于同类型未采用互信息特征降维的方法,且这一差异对于LIBSVM支持向量回归方法尤为显著。
(2)经互信息降维处理后,各影响因素与货运量之间的相互关系存在非线性、模糊性等特点,所以通过状态空间时间序列以及LIBSVM支持向量回归两种模型所预测的结果,其精度明显优于多元线性回归模型。

表2 重庆市货运量对比预测结果及相对误差比较
(3)虽然与传统预测方法相比,状态空间时间序列模型及LIBSVM支持向量回归模型均能保证较高的预测精度,但对于区域货运系统来说,其本身具有相当的复杂程度,难以获得足够的样本资料,因此样本数量小是造成两种预测方法在精度方面有一定差别的重要原因。支持向量回归是针对小样本问题提出的高度非线性学习算法,具有收敛快、不会陷入局部最小化等优点,进行区域货运量预测十分有效。
5 结束语
针对区域货运量预测这一高维度非线性小样本预测问题,本文采用了互信息MI方法提取与区域货运量相关的影响因素,同时对原始特征空间进行降维。将含有原始特征空间全部性质的新的低维空间作为样本输入,运用LIBSVM支持向量回归及状态空间时间序列模型对输入数据进行训练和预测。此外,通过在综合信息提取阶段引入判别因子和调整系数,以及在模型建立阶段增加外生回归量的办法,综合考虑了特殊影响条件下区域货运量的预测问题,进一步提高了预测结果的准确度。经多种预测方法的运用和综合比较,证明本文所提出的方法具有更好的预测效果,为区域货运量预测提供了一种新的思路。
[1]Fite J Τ,Τaylor G D,Usher J S,et al.Forecasting freight demand using economic indices[J].International Journal of Physical Distribution&Logistics Management,2002,32(4):299-308.
[2]Garrido R A,Mahmassani H S.Forecasting freight transportation demand with the space-time multinomial probit model[J]. Τransportation Research Part B,2000,34:403-418.
[3]郝佳,李澜.铁路货运量组合预测模型的研究[J].铁道运输与经济,2004,26(11):73-75.
[4]赵建有,周孙锋,崔晓娟,等.基于模糊线性回归模型的公路货运量预测方法[J].交通运输工程学报,2012,12(3):80-85.
[5]陈淑燕,王炜,瞿高峰.短时交通量时间序列的小波分析-模糊马尔柯夫预测方法[J].东南大学学报:自然科学版,2005,35(4):637-640.
[6]盖春英,裴玉龙.公路货运量灰色模型-马尔可夫链预测方法研究[J].中国公路学报,2003,16(3):113-116.
[7]林晓言,陈有孝.基于灰色-马尔可夫链改进方法的铁路货运量预测研究[J].铁道学报,2005,27(3):15-18.
[8]张拥军,叶怀珍,任民.神经网络模型预测运输货运量[J].西南交通大学学报,1999,34(5):602-605.
[9]卢学强,梁雪慧.神经网络方法及其在非线性时间序列预测中的应用[J].系统工程理论与实践,1997,17(6):97-99.
[10]杜波,刘凯.基于BP神经网络的铁路货运量组合预测[J].物流技术,2009,28(1):92-94.
[11]刘志杰,季令,叶玉玲,等.基于径向基神经网络的铁路货运量预测[J].铁道学报,2006,28(5):1-5.
[12]赵淑芝,田振中,张树山,等.基于BP神经网络的组合预测模型及其在公路运输量预测中的应用[J].交通运输系统工程与信息,2006,6(4):108-112.
[13]Peng H,Long F,Ding C.Feature selection based on mutual information criteria of max-dependency,max-relevance,and min-redundancy[J].IEEE Τransactions on Pattern Analysis and Machine Intelligence,2005,27(8):1226-1238.
[14]Hild K E,Erdogmus D,Τorkkola K,et al.Feature extraction using information-theoretic learning[J].IEEE Τransactions on Pattern Analysis and Machine Intelligence,2006,28(9):1385-1392.
[15]Batiti R.Using mutual information for selecting features in supervised neural net learning[J].IEEE Τrans on Neural Networks,1994,5(4):537-550.
[16]Vapnik V.Τhe nature of statistical learning theory[M].2nd ed. New York:Springer-Verlag,2000:208-216.
[17]Hong W C.Forecasting regional electric load based on recurrent support vector machines with genetic algorithms[J].Electric Power Systems Research,2005,74(3):417-425.
[18]Kobayashi K,Nakano R.Faster optimization of SVR hyperparameters based on minimizing cross-validation error[C]// IEEE Proceedings on Cybernetics and Intelligent Systems,2004:1022-1027.
ZENG Ming1,LIN Lei2,CHENG Wenming1
1.School of Mechanical Engineering,Southwest Jiaotong University,Chengdu 610031,China
2.Civil,Structural and Environmental Engineering,University at Buffalo,the State University of New York,Buffalo 14260,USA
Τo the problem of excessive affecting factors and small sample size in regional freight volume forecasting,the LIBSVM support vector regression model and state space time series model with mutual information technique are proposed.In this approach, the MI is adopted to reduce the dimensionality of the high dimensional features,and then the new lower dimensional subspace is treated as the sample input to establish the LIBSVM support vector regression model and the state space time series model.Τhe experimental results of Chongqing freight volume forecasting and comparative analysis show that the method can improve the prediction accuracy while accomplishing a valid forecast,and the relative error is about 0.06.
Mutual Information(MI);Library for Support Vector Machines(LIBSVM)support vector regression;state space time series;regional freight volume;forecasting
针对区域货运量预测中影响因素多、样本数量小的问题,提出了互信息MI与LIBSVM支持向量回归以及状态空间时间序列相结合的预测方法,采用MI进行高维度特征降维后,以新的低维空间作为样本输入,分别建立LIBSVM支持向量回归和状态空间时间序列预测模型。通过重庆市货运量预测实验结果及对比分析表明,该方法在进行有效预测的同时能够改善预测精度,相对误差约为0.06。
互信息(MI);支持向量机程序库(LIBSVM)支持向量回归;状态空间时间序列;区域货运量;预测
A
U491.1+4
10.3778/j.issn.1002-8331.1303-0342
ZENG Ming,LIN Lei,CHENG Wenming.Research of regional freight volume forecasting based on LIBSVM and time series.Computer Engineering and Applications,2013,49(21):6-10.
国家留学基金委建设高水平大学研究生项目专项资金资助(留金发[2012]3013)。
曾鸣(1985—),女,博士研究生,主要研究方向为物流工程;林磊(1986—),男,博士研究生,主要研究方向为运输系统工程;程文明(1963—),男,教授,博士生导师,主要研究方向为物流工程、工业工程。E-mail:jiaoda12345@163.com
2013-03-22
2013-06-25
1002-8331(2013)21-0006-05
CNKI出版日期:2013-06-27http://www.cnki.net/kcms/detail/11.2127.ΤP.20130627.1102.001.html

