面向多峰函数优化的PASFLI算法及应用

李国平

湖南工学院，湖南衡阳 421002

面向多峰函数优化的PASFLI算法及应用

李国平

湖南工学院，湖南衡阳 421002

混合蛙跳算法（Shuffled Frog Leaping Algorithm，SFLA）是Eusuff等人根据混合竞争进化思想，提出的一种新型智能启发式计算技术[1]。由于该算法具有实现简单、前期收敛速度快、搜索能力强等特点，已被成功应用于复杂非线性函数优化以及车间流水调度、ΤSP等工程领域[2-3]。目前，改善算法复杂问题优化性能已成为研究热点之一[4-9]。

针对基本SFLA求解复杂优化问题时存在后期收敛速度慢、早熟收敛等[6]缺陷，学者进行了大量研究，提出了相应的改进方法。常见的改进策略是通过修改SFLA参数以提高算法收敛性能，如采用线性递减调整惯性权重[4]、搜索加速因子[5]来协调全局和局部搜索能力；也有的通过引入其他智能算子，如自适应混沌变异算子[6]、领域正交叉算子[7]、多种群协同进化[8]等形成混合智能蛙跳算法；还有的通过增加子种群多样性，如EO-SFLA[9]来增强SFLA全局寻优能力。这些改进策略不同程度地改善了算法性能，但是由于SFLA提出时间不长，相应理论分析较少，特别是对于复杂高维多峰函数优化问题，收敛效果不理想仍是SFLA面临的难题。

免疫克隆选择算法（Clonal Selection Algorithm，CSA）是生物免疫理论重要算法之一[10]。CSA能够实现局部与全局同步搜索，有效地避免了早熟和陷入局部极值，特别是在算法运行后期，随着亲和度的提高，CSA能够很快地收敛于全局极值而且具有较高的精度[11]。CSA的缺陷在于对初始值比较敏感，算法运算初期收敛效率不高。文献[12]对CSA与SFLA协同进化进行了尝试，但是其组合方式仍属于多种群独立协同进化范畴。针对基本SFLA在高维多峰函数优化时早熟及难以找到所有全局极值的缺陷，利用SFLA及CSA各自优势，提出了自适应混合蛙跳免疫算法（Polymorphic Adaptive Shuffled Frog Leaping Immune Algorithm，PASFLIA）。算法采用双层进化模式，在低层混合蛙跳操作中，加入多态自适应子种群机制，将子种群动态地划分为精英群和扩散群；在算法进化后期，提出全局极值筛选策略，将子种群极值点提升到高层进行免疫克隆选择操作。仿真结果表明PASFLIA在高维多峰函数优化方面取得了良好效果。

1 PASFLIA算法实现

PASFLIA采用两层进化模型（如图1所示），低层为青蛙粒子种群集合SF={E1，E2，…，EM}，SF又划分为M个子种（族）群；高层为免疫抗体种群C。更新操作是指一方面将低层子种群个体极值提升到高层，另一方面将高层经过CSA操作后的个体极值更新低层中对应的个体极值。

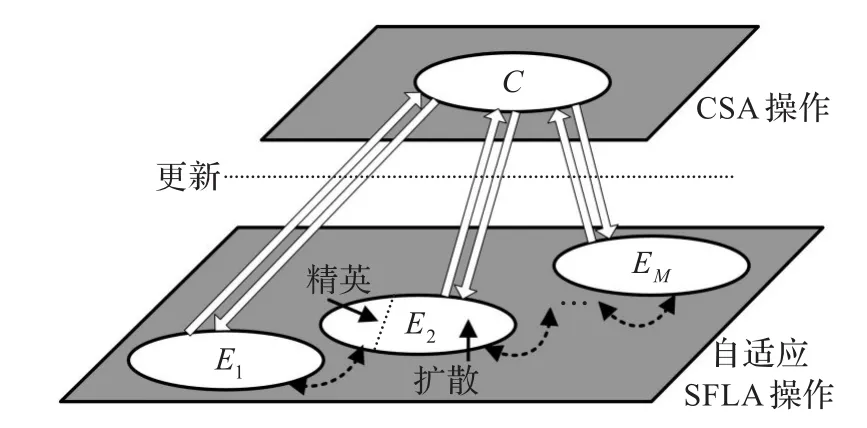
图1 PASFLIA算法模型

1.1 多态子种群自适应SFLA操作

基本SFLA工作过程可以描述为：由F只青蛙组成的种群SF，对于n维优化问题，每只青蛙代表优化问题的一个解，第k只青蛙位置为Xk={xk1，xk2，…，xkn}。计算每只青蛙的适应度值f(Xk)[11]并按降序排列，然后平均分配到M个子种群Ei(1≤i≤M)中，每个子种群青蛙数为N。Ei按式（1）进行划分。

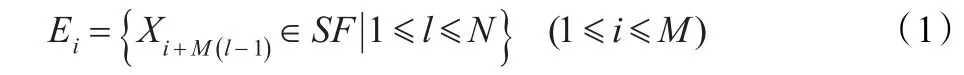
SFLA对子种群Ei中适应度值最差的解Xi，w按式（2）进行更新。

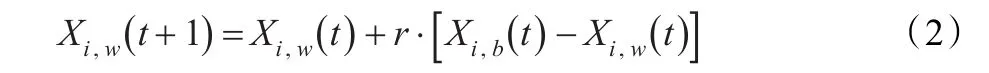
其中，r∈[0，1]且为随机数，Xi，b为Ei当前适应度最好的解。如果f[Xi，w(t+1)]优于f[Xi，w(t)]，则用新位置替代旧位置，否则用Xg（Xg为当前青蛙群体中适应度最好的解）代替Xi，b执行更新策略（2），如果结果仍然不能优于旧位置，则生成随机青蛙取代Xi，w。Ei重复执行局部搜索过程，直到局部搜索迭代次数为止。当所有子种群完成搜索后，所有青蛙重新组合，然后重新划分族群，重新进行局部搜索，并更新群体最优解位置，直到满足终止条件。

研究表明，随着迭代次数增加，SFLA收敛效率明显降低。这是因为，在算法运算后期，当某个青蛙粒子为当前最优位置时，其他青蛙会向其聚拢，特别是如果该位置为局部极值点，则算法就会很容易陷入局部极值，需要迭代较多次数才能跳出[9]，并出现早熟现象。为了提高基本SFLA算法收敛速度和避免早熟，本文提出了多态子种群机制：将子种群Ei按适应度值降序排列，适应度值较优的青蛙粒子划分到精英群，剩余的为扩散群。精英群内的青蛙粒子具有较优的适应度值，因此对其采用精英学习机制，使得粒子能够以更大的概率跳出局部极值；扩散群内的青蛙粒子采用改进的粒子更新策略，充分利用了历史信息，扩大了样本多样性和搜索空间。

定义1（子种群划分规模确定因子D() t）

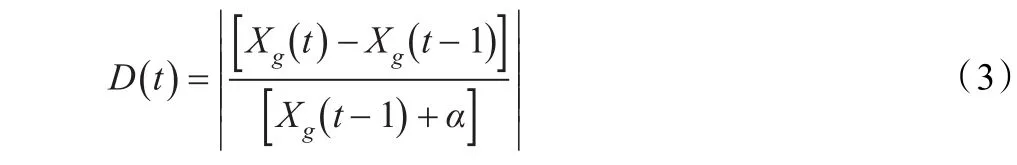
其中，α为取值极小的正数。当D(t)=0时表示进化停止。定义D(t)之后，扩散群规模由式（4）确定。

其中，Ni，s(t)为Ei内的扩散群规模，ω为规模控制系数。为了避免Ni，s(t)的数值过大或者过小，设定Nmin≤Ni，s(t)≤Nmax。从式（3）、（4）可以看出，进化初期D(t)取值较大，扩散群规模较小。随着迭代次数增加，D(t)取值逐渐减少，这表明种群样本多样性降低，Ni，s(t)规模变大，因此算法可以用更多的扩散粒子去增加样本多样性，提高搜索空间。

定义2（扩散群青蛙粒子更新策略）

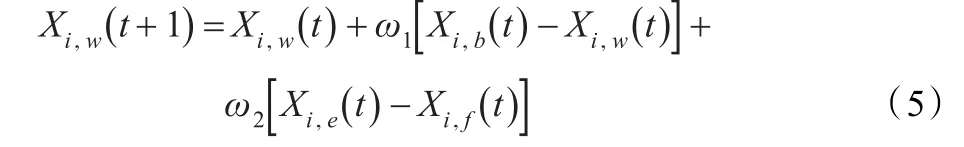
其中，Xi，e、Xi，f为Ei中随机抽取的个体(e≠f≠b≠w)，式（5）在式（2）的基础上增加了其他个体信息，扩大了样本空间。如果上式不能产生更优解，则生成随机青蛙替代旧粒子。

精英群Ni，L(t)规模可由式（6）确定。

定义3（精英群精英学习机制）

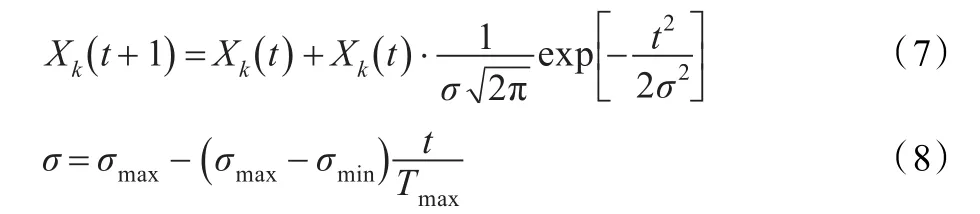
其中，Tmax为算法最大迭代次数。精英学习机制实质为具有自适应的高斯变异，随着迭代次数增加，σ逐渐减小。采用式（7）更新方式，使得青蛙粒子在算法初期能够在较大学习空间内搜索，更容易跳出局部极值；在算法后期，青蛙粒子在较小的学习空间内进行较精细度搜索，有利于提高算法精度。

1.2 高层CSA操作

定义4（同峰判断准则）

对于多峰函数f(x)，xa、xb为函数的两个全局极值点，在两点之间均匀插入l-1个点，得到l+1个点组成的集合L={xa，xa+1，…，xb}。依次从L集合中取两两相邻的点xn、xn+1(a≤n〈b)，若式（9）值出现由正变负，则说明xa、xb为异峰全局极值点，否则为同峰全局极值点。

全局极值筛选策略：设子种群Ei极值点集合为Pi= {Xj}，j∈(i·N，(i+1)·N]，全局极值点结合为Pi，min。取Xi，b为Pi，min第一点，然后依次从集合Pi中取点Xj，如果满足式（10），则Xj为全局极值点。

其中，f(a)为理论全局极值，ε为已设定常数。如果Xj满足式（10），将其与Pi，min的点依次判断是否同峰。如果同峰且适应度值优于已存在的点，则用Xj替代该点，若为异峰，则将Xj加入到Pi，min中。

定义5（亲和度）定义混合蛙跳算法的适应度函数为免疫克隆亲和度函数。即

高层CSA操作种群C={ai}由低层个子种群Pi，min组成。高层CSA操作工作过程为：

（1）克隆扩增：对于Pi，min中的抗体按照式（12）进行克隆扩增。

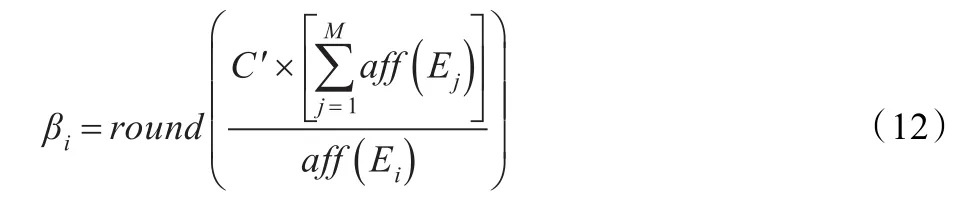
其中，aff(Ej)为低层Ej中最优个体亲和度值。由式（12）可以看出，适应度值越优的子种群其克隆倍数越大，使得具有高亲和力的抗体获得了更多的克隆机会。

（2）自适应变异：克隆后的抗体按照式（13）进行高斯变异。

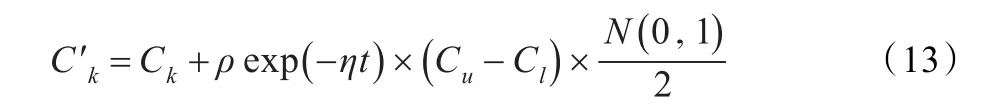
其中，ρ、η为调节系数，Cu、Cl为Ck上下限。上式表明，进化初期，粒子在较大空间内变异。随着迭代次数增加，算法将在小范围内进行精细搜索。

（3）免疫选择。对于抗体Ck(t)，其经过克隆及变异得到的抗体集合为S，取S中亲和度最优个体C′k(t)，并判断C′k(t)是否优于Ck(t)，若是，则Ck(t+1)←C′k(t)，否则Ck(t)保持不变。这种选择机制确保了子种群最优解不会变得更差。

2 PASFLIA收敛性及算法流程

2.1 PASFLIA收敛性

文献[9]给出了基本SFLA算法的收敛性证明，并指出SFLA依概率1收敛于全局最优解，在此基础上，本文就PASFLIA算法收敛性进行分析。对于随机算法G、优化问题〈S，f〉（S为可行解空间，f为适应度函数），Xk表示第k次迭代结果，第k+1次结果Xk+1=G() Xk，δ（δ为算法G搜索过的解）。

条件1（假设函数f为最小化函数优化问题）

f(G(X，δ))≤f(X)，并且如果δ∈S，则有f(G(X，δ))≤f(δ)。

综上所述，PASFLIA具有全局收敛性，证毕。

2.2 PASFLIA算法实现流程

PASFLIA算法主要流程的伪码描述如下：

步骤1算法设置：设置种群规模F，子族群数量M，精英群与扩散群规模控制系数ω，最大迭代次数。

步骤2初始化：随机产生规模为F的青蛙初始种群，迭代次数t←0。

步骤3低层自适应SFLA操作：青蛙粒子按适应度值降序排列，根据式（1）划分子种群；

步骤3.1局部收索：对于每个子种群Ei，根据式（4）、（6）确定精英群和扩散群规模；根据式（7）对精英群内粒子进行更新，根据式（5）对扩散群最差个体进行更新。

步骤3.2局部迭代停止判断：判断局部迭代次数是否满足，不满足继续局部搜索。

步骤3.3个体极值集合Pi与全局极值集合Pi，min更新。

步骤4是否进入高层CSA操作判断：如果迭代次数t≤tC（tC为高层开始迭代次数），t←t+1，转步骤3；否则进入高层CSA操作。

步骤5高层CSA操作：

步骤5.1根据式（12）对克隆抗体克隆，根据式（13）对抗体进行变异，免疫选择操作。

步骤5.2更新子种群极值点，转步骤3。

步骤6算法停止判断：判断算法是否满足终止条件，是输出结果，算法结束；否则转步骤3。

3 仿真实验

3.1 实例仿真

为了验证PASFLIA算法性能，在Matlab7.0仿真平台上，采用以下多峰函数进行仿真，其中f1为单模态函数，f2具有少量局部极值，f3～f6具有大量局部极值。PASFLIA算法参数设置为：F=500，M=10，N=50，ω=0.75，ω1=0.8， ω2=0.2，ε=1×10-4，局部迭代10次，全局迭代500次。

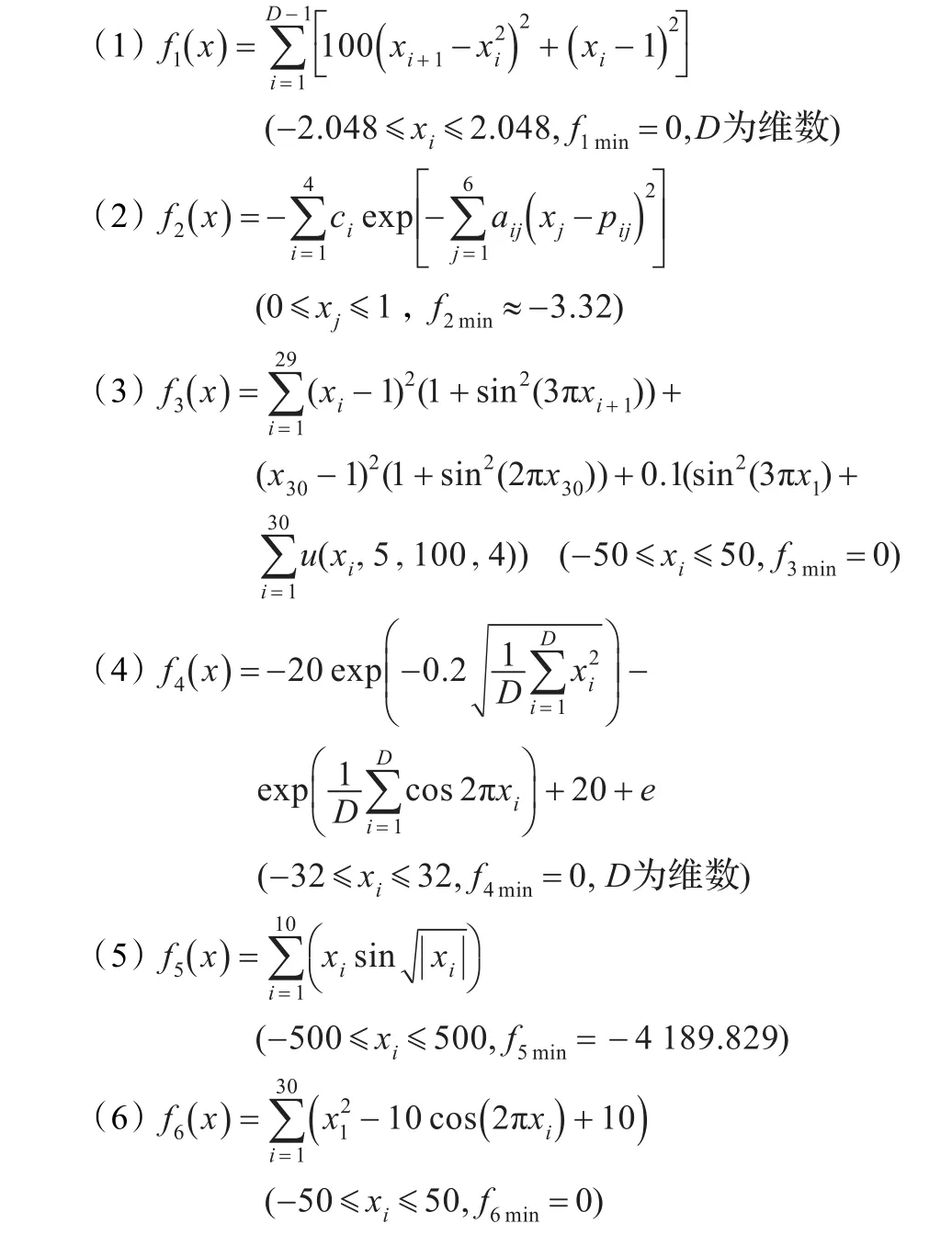
为进一步分析PASFLIA在高维复杂函数下的寻优能力，将其应用于多维函数f1、f4优化过程中。仿真实验设定不同的维数（由于篇幅限制D取1 000和5 000），并与算法PASFLA和ASFLIA进行比较。图4给出了D=5 000时的函数收敛曲线，表2给出了高维情况下PASFLIA算法与其他两种算法对比结果。

3.2 PASFLIA性能分析

从表1可以看出，PASFLIA各项对比指标明显优于PASFLA及ASFLIA算法。除函数f3外，PASFLIA都找到了函数的理论最优值，而其他两种算法均未找到函数的理论最优值。从图2、3可以看出，PASFLIA收敛效率明显高于其他两种算法，在500次迭代内完成了寻优运算，此外ASFLIA的收敛性能要优于PASFLA算法，这说明免疫克隆选择操作对算法运算后期提高收敛能力具有一定的效果。从表2和图4可以看出，与其他两种算法相比，PASFLIA在高维函数优化过程中效果更佳突出，随着函数维数的增加，PASFLIA收敛精度并没有明显降低，迭代次数没有明显增加。

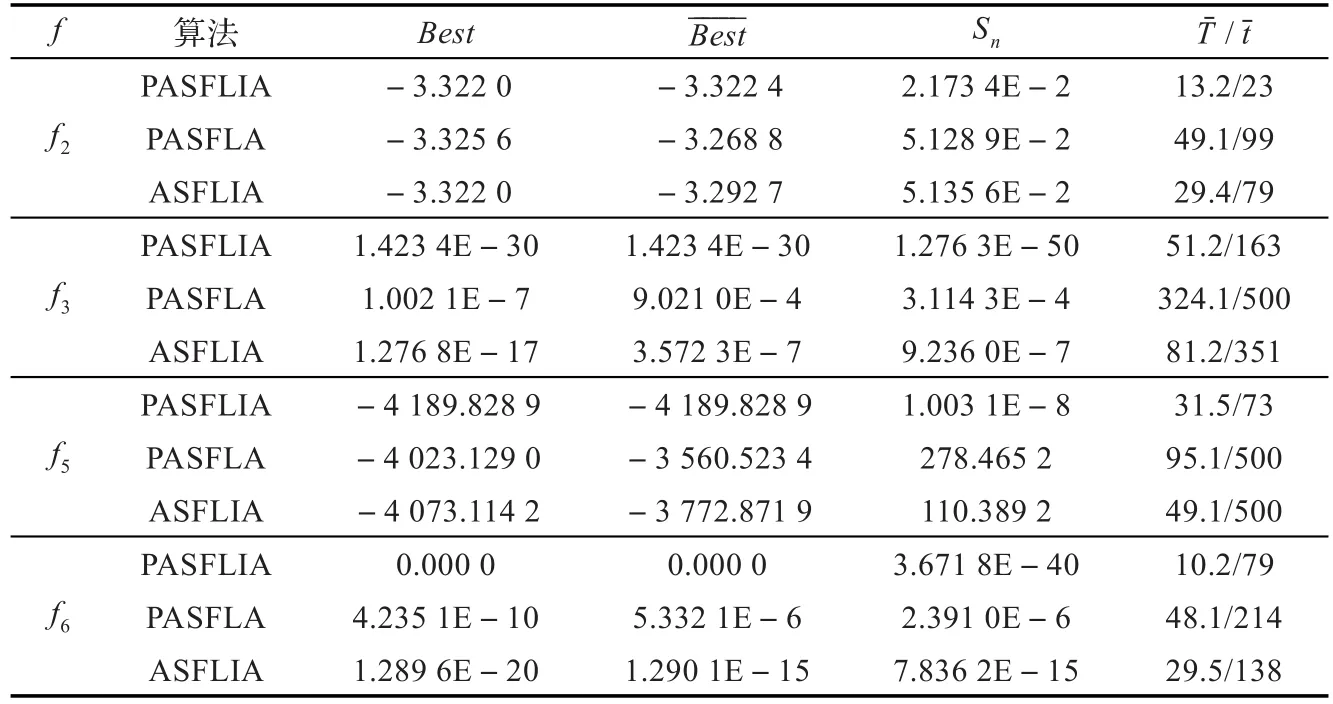
表1 PASFLIA算法与其他两种算法对比

图2 f2、f3函数收敛曲线

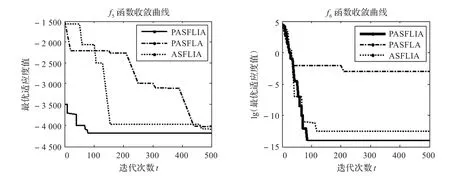
图3 f5、f6函数收敛曲线

图4 维数为5 000时f1、f4函数收敛曲线

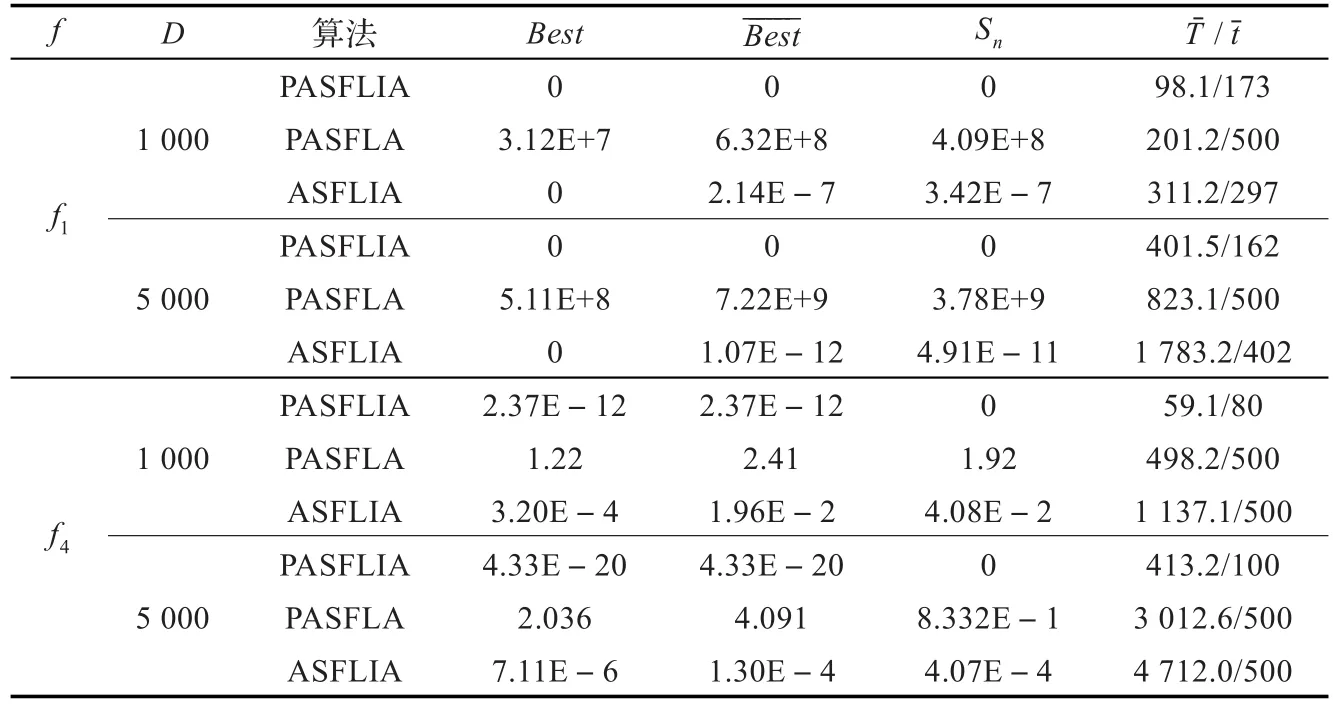
表2 高维情况下PASFLIA算法与其他两种算法对比

PASFLIA之所以具有突出的优化能力，是因为多态子种群自适应的使用，改善了算法在运算后期样本多样性，精英学习机制的引入提高了算法跳出局部极值的能力，免疫克隆选择操作进一步提高了算法求解复杂多维函数的性能。此外，全局机制筛选策略保证了算法能够找出多峰函数的全部全局极值点。

4 结语

对混合蛙跳算法改进及在复杂多峰优化中的应用问题进行了研究。提出了具有双层进化模式的多态子种群自适应混合蛙跳免疫算法。加入了多态自适应子种群机制，在算法进化后期，给出了全局极值筛选策略，并分析了算法的全局收敛性。复杂多峰函数仿真实验表明，多态子种群自适应机制及免疫克隆选择操作扩大了种群样本空间，平衡了全局与局部的关系，明显增强了算法求解复杂多维函数的能力。

[1]Eusuff M M，Lansey K E.Optimization of water distribution network design using the shuffled frog leaping algorithm[J]. Water Resources Planning and Management，2003，129（3）：210-225.

[2]Rahimi-Vahed A，Mirzaei A H.A hybrid multi-objective shuffled frog-leaping algorithm for a mixed model assembly line sequencing problem[J].Computers and Industrial Engineering，2007，53（4）：642-666.

[3]罗雪晖，杨烨，李霞.改进混合蛙跳算法求解旅行商问题[J].通信学报，2009，30（7）：130-135.

[4]刘悦婷.带有选择和自适应变异机制的混合蛙跳算法[J].计算机工程，2012，38（23）：206-210.

[5]Elbeltagi E，Hegazy Τ，Grierson D.A modified shuffled frogleaping optimization algorithm applications to project management[J].Structure and Infrastructure Engineering，2007，3（1）：53-60.

[6]葛宇，王学平，梁静.自适应混沌变异蛙跳算法[J].计算机应用研究，2011，28（3）：945-947.

[7]孟庆莹，王联国.基于领域正交叉算子的混合蛙跳算法[J].计算机工程与应用，2011，47（36）：54-56.

[8]Niknam Τ，Farsani E A.A hybrid evolutionary algorithm for distribution feeder reconfiguration[J].Science China：Τechnological Sciences，2010，53（4）：950-959.

[9]骆剑平，陈泯融.混合蛙跳算法及其改进算法的运动轨迹及收敛性分析[J].信号处理，2010，26（9）：1428-1433.

[10]刘芳，潘晓英.基于免疫克隆选择的块匹配运动估计[J].软件学报，2007，18（4）：850-860.

[11]吴建辉，章兢，李仁发，等.多子种群微粒群免疫算法及其在函数优化中应用[J].计算机研究与发展，2012，49（9）：1883-1898.

[12]Antariksha B.A clonal selection based shuffled frog leaping algorithm[C]//IEEE Int Advance Computing Conf.New York：IEEE Press，2009：125-130.

LI Guoping

Hunan Institution of Τechnology,Hengyang,Hunan 421002,China

As basic Shuffled Frog Leaping Algorithm（SFLA）has many problems in the high dimensional multimodal function optimization such as premature and difficult to find all global extremes,a hybrid intelligent Polymorphic Adaptive Shuffled Frog Leaping Immune Algorithm（PASFLIA）is presented.PASFLIA which combines the SFLA and immune Clonal Selection Algorithm （CSA）technology is convergent to the global optimal solution with probability 1.PASFLIA adopts a double-layer model evolution:in the lower layer,the polymorphic adaptive population mechanism is joined to SFLA,which improves the diversity of the population,and effectively suppresses premature behavior of the convergence progress;in the higher layer,the global extreme screening strategy is proposed,which puts the population extreme points to high-level immune clonal selection operation,further enhancing the global optimization ability.Τhe complex multimodal function simulation experiments results show that the PASFLIA can quickly and efficiently give all the global optimal solution.

shuffled frog leaping algorithm;immune algorithm;adaptive;function optimization

针对基本混合蛙跳算法在高维多峰函数优化时早熟及难以找到所有全局极值的问题，提出了一种具有混合智能的多态子种群自适应混合蛙跳免疫算法，证明了算法以概率1收敛于全局最优解。该算法采用双层进化模式，融合了混合蛙跳、免疫克隆选择技术。在低层混合蛙跳操作中，加入了多态自适应子种群机制，提高了子种群多样性，有效抑制了早熟现象；在算法进化后期，提出了全局极值筛选策略，将子种群极值点提升到高层免疫克隆选择操作，进一步提高了全局寻优能力。通过复杂多峰函数仿真实验，表明该算法能够快速有效地给出全部全局最优解。

混合蛙跳算法；免疫算法；自适应；函数优化

A

ΤP183

10.3778/j.issn.1002-8331.1306-0061

LI Guoping.PASFLI algorithm for multimodal function optimization and its application.Computer Engineering and Applications,2013,49（21）：199-203.

李国平（1979—），男，讲师，主要研究方向：数值最优化和智能处理。

2013-06-08

2013-09-16

1002-8331（2013）21-0199-05