差异工件流水车间批调度问题的求解
朱颀,陈成栋,陈华平
中国科学技术大学 管理学院,合肥 230026
差异工件流水车间批调度问题的求解
朱颀,陈成栋,陈华平
中国科学技术大学 管理学院,合肥 230026
1 引言
差异工件流水车间批调度问题是工业生产中一类典型的调度问题。它是对传统流水车间问题的进一步扩展,即在流水车间的每个阶段均是批处理机。求解该问题分为两个步骤:首先工件遵循特定分批规则成批,然后将形成的批按照相同的加工顺序在各批处理机上逐个进行加工。这类组合优化问题在实际应用中很常见,如电子工业的环境应力筛选过程就可抽象为一个典型的流水车间批调度问题。环境应力筛选由半导体工业的老化实验发展而来,整个产品需要在用户设定的不同环境下进行测试,每个筛选实验箱可以看做一个批处理机,数量由待测试的装配车间的数量以及特定装备车间的测试数量决定。该问题的研究具有很好的现实意义。
目前关于求解流水车间批调度问题的研究大部分限于两台机器的情况,求解目标多为最小化制造跨度(Makespan)。如Mirsanei等[1]在ARA和FLA两种启发式算法以及模拟退火算法(SA)的基础上提出ARSA和FLSA两种改进算法;Purushothaman等[2]采用遗传算法(GA)进行了求解;Alebachew等[3]在工件顺序的模糊调度模型基础上提出了基于GA的求解思路;Liao等[4]采用禁忌搜索算法(TS)对问题进行了求解,并与混合整数线性规划进行了比较;针对多机器的情况(即3台批处理机及以上),Ali等[5]提出了一种改进的混合整数线性规划方法(Mixed Integer Linear Formulation),在小规模工件的情况下进行了求解。目前鲜有利用智能算法对此问题的求解。
本文研究了流水车间批调度问题在大规模工件情况下的求解,考虑到群智能算法在求解大规模工件问题上的优势,将微粒群算法(PSO)[6]引入差异工件流水车间批调度问题的求解,提出了一种改进的微粒群算法。为保证种群具备一定的分散度和质量,采用基于NEH方法的种群初始化方法,并利用ROV规则[7]将微粒的连续位置转化为离散的加工顺序。由于传统微粒群算法容易陷入局部最优,形成早熟收敛的情况,在粒子群算法每次迭代过程中引入一种局部搜索技术(Variable Neighborhood Search,VNS)[8],并采用了一种自适应惯性权系数(Adaptive Inertia Weight Factor,AIWF)[8]改进原惯性权系数。最后通过生成的基准测试算例,将改进的PSO算法与该问题的一个下界(Lower Bound,LB)[5]和启发式算法中效果最好的Nawaz-Enscore-Ham(NEH)算法[9],以及标准的PSO算法进行了比较,并验证了算法的有效性。
2 问题描述
差异工件的流水车间批调度问题的具体描述如下:
(1)流水车间的每个阶段均是一台批处理机,可同时将多个工件作为一批同时进行加工;
(2)工件遵循特定分批规则加入相应批后按照相同的加工顺序同时在批处理机上进行加工,一旦形成特定的批则工件不能加入或者移除出批;
(3)每个批的最大容量均相同,批中工件的尺寸之和不能超过批的最大容量限制;
(4)批的加工时间为批中加工时间最长的工件的加工时间;
(5)批在加工时不允许中断;
(6)假定每个批之间存在一个无限大的缓冲区。
根据调度问题的三参数表示法,该问题可表示为Fm|B,sj| Cmax,数学模型如下:

式(1)中,Cmax表示最大制造跨度,即Makespan。式(2)确保每个工件都在一个特定的批中,若工件j在批b中,则Xjb=1,否则Xjb=0。式(3)中,sj为工件j的尺寸,B为批容量,确保批中的工件尺寸总和不超过批容量。式(4)给出了批加工时间的约束条件,Pij表示批i在第j台批处理机上的加工时间,pij为工件i在第j台机器上的加工时间,表示批的加工时间为批中加工时间最长的工件的加工时间。式(5)和式(6)确保批b只能在加工次序的某个位置,并且每个加工次序的某个位置上只能有一个批;若批b在加工次序i调度,Zbi=1,否则Zbi=0。式(7)决定了在机器i上的第b批的加工时间,Qbi表示第b批在机器i上的加工时间。如果Zbi=1,则Qbi≥Pbi,由于问题目标是求出最小的时间跨度,因此Qbi=Pbi;如果Zbk=0,则Qbi≥Pbi-BigM,若想得到最小的Cmax,Qbi=0。式(8)表示了工件在机器1上第b阶段的加工时间;Cb1表示第b批在机器1上的完成时间,Qk′1表示第k′批在机器1上的加工时间。式(9)~式(11)给出了求解最小制造跨度的递归方程,式(9)中C1i表示第1台机器上第i批的完成时间,Q1i′表示第1台机器上第i′批的加工时间。式(10)表示第i批在机器l上的完成时间Cli,为第i-1批在机器i上的完成时间Cl,i-1与第i批在机器l上的加工时间Qli之和。同理,式(11)表示第i批在机器l上的完成时间Cli,为第i批在第l-1台机器上的加工时间Cl-1,i与第i批在机器l上的加工时间Qli之和。式(12)表示制造跨度Cmax为最后完成的加工批的完成时间。
3 流水车间批调度问题的求解
差异工件流水车间批调度问题的求解可分为两个部分。首先是对差异工件进行分批,差异工件的批调度问题是由Uzsoy在1994年首先提出,并证明了该问题是NP难的[10]。考虑到差异工件分批可能导致的批的加工时间分配不合理以及批的空间浪费问题,采用Palmer启发式算法[11]对工件进行初始排序,然后利用BF(Best Fit)分批规则对其进行分批。
由于成批后不能加入新工件或者将批内工件移除出批,则每个批可看做一个独立的工件,因此后续的加工问题等价于置换流水车间调度问题,即批的排序问题。当流水车间的机器数量为2台时,可在多项式时间内得到解答,而机器数量大于2台的情况已被证明为NP难题[12]。近年来PSO算法在求解大规模优化问题上获得了广泛应用和认同,本文对传统的PSO算法进行了改进,来对批的排序进行求解。
3.1 差异工件的分批
为了提高分批质量,采用目前分批效果较好的BF分批规则进行分批,并在分批之前采用Palmer启发式算法初始化工件序列。
Palmer算法是基于斜度指标(Slope Index)排序工件的启发式算法。根据流水车间工件的加工顺序,加工时间趋于增加的工件被赋予较大的优先权数。工件i的斜度指标(Slope Index)Si定义为:

其中,m为机器数目,pij为第i个工件在第j台机器上的加工时间。按照Si递减的顺序对工件进行初始排序。
对获得初始排序的工件序列采用BF规则进行分批,得到初始批序列。BF分批规则为:选择处于工件序列顶端的工件,并将之放入之前形成的批序列中剩余空间最小的批中。如果工件无法放入任何一个存在的批中,则创建新的批,直到工件序列中的工件全部加入批为止。形成的批序列即为初始批序列。由于工件均遵循相同的加工顺序,则每个批在每台机器上的加工顺序也是相同的。批在每台机器上的加工时间为批中在每台机器上加工时间最长的工件的加工时间。此时问题转化为置换流水车间调度问题。
3.2 基于改进的PSO算法的批排序方法
微粒群算法是基于群智能理论的一种新型演化计算技术。其基本思想是通过群体中个体之间的协作与信息共享来搜索最优解,本质上是一种并行的全局性随机搜索算法,搜索过程保留了局部个体和群体的最优信息,体现了协同搜索的优势。但是微粒群算法也有局部搜索能力较差,易陷入局部极小解等缺点。考虑到变邻域搜索算法能够帮助微粒在更大的解空间进行搜索,同时结合流水车间调度问题的自身特点,提出了基于自然数编码的改进微粒群算法。算法的总体结构,如图1所示。

图1 算法总体结构图
3.2.1 微粒编码
流水车间批调度问题的编码方式类似置换流水车间,这里采用最常用的编码方式,即直接采用批的排序。对于批的个数为n的问题,微粒采用n维向量表示,每个批对应微粒的某一维度。由于微粒群算法的微粒的位置为连续值矢量,标准微粒群算法是无法实现批的排序更新的。因此这里构造从微粒的位置矢量到批的排序的映射机制,利用微粒的位置值的大小关系,结合随机键编码,将微粒的连续位置Xi=[xi,1,xi,2,…,xi,n]转换为离散的加工顺序π=[πi,1,πi,2,…,πi,n],即每个批在机器上的加工顺序。
应用ROV规则实现微粒位置矢量到批的排序的映射。该规则具体描述如下:对于某个微粒的位置矢量,首先将最小的位置矢量赋予ROV值1,将第二小的位置矢量赋予ROV值2,依此类推,直到所有的位置矢量均获得唯一的ROV值,从而基于ROV值可得到批的一个加工顺序。
例假设微粒Xi的位置为5维矢量,即Xi=[4.27,1.83,0.99,3.25,0.07],则首先赋予最小值xi,5的ROV值为1,同理,赋予xi,3的ROV值为2,依此类推,可得批的加工顺序π=[5,3,2,4,1],如表1所示。
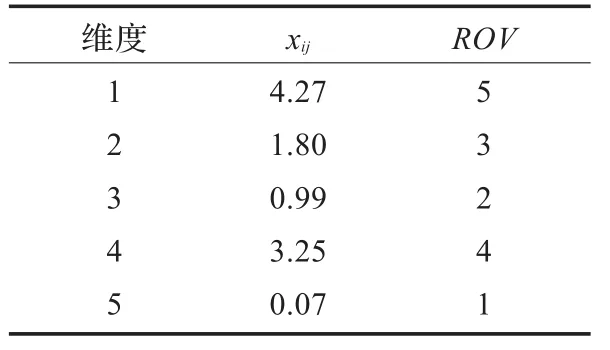
表1 微粒位置矢量对应的ROV值
对于每个微粒,根据其位置矢量对应的ROV值确定每个批的加工顺序,在m台机器的情况下,加工顺序遵循j1,j2,…,jn的流水车间批调度问题,可由如下递归方程得到问题的Makespan:

其中,Ci,j1表示在机器i上第j1个批的完成时间;pi,jk表示第i台机器上第jk个批的加工时间。
3.2.2 微粒的位置更新公式
微粒群算法中,每个粒子均在n维空间中以一定的速度飞行,每个微粒根据自身以及其他粒子的飞行经验动态调整自身的位置和速度。n维搜索空间中第i个微粒的位置和速度可分别表示为Xi=[xi1,xi2,…,xin]和Vi=[vi1,vi2,…,vin]。通过评价各个微粒的目标函数,确定第k次迭代每个微粒所经过的最佳位置(pbest)Pi=[pi1,pi2,…,pin]及微粒群体所发现的最佳位置(gbest)Pg,再按照如下公式更新各个微粒的速度和位置:

其中w为惯性权系数,r1和r2为0到1的随机数,c1和c2为正的加速常数。
3.2.3 微粒的初始化和参数设置
标准的微粒群算法通常采用随机生成微粒的方式进行初始化。但是为了使初始种群具备一定的分散度和质量,采用目前为止性能最优的NEH启发式方法对种群进行初始化,种群规模设置为微粒维度的3倍。
NEH启发式算法假定在所有机器上的总加工时间越长的工件,比总加工时间短的工件具有更高的优先级,具体步骤如下:
(1)按照在所有机器上总加工时间递减的顺序排列n个批。
(2)选择前两个批进行排序,直到在只有两个批的情况下获得最小的局部Makespan的排序为止。
(3)对余下的k个批,k=3,4,…,n,依次插入到前面所获排序的k个位置上,直到每次插入均获得最小局部Makespan为止;最后可得到整个批序列的NEH排序结果。
利用NEH启发式算法产生第一个微粒的初始位置:
由于NEH算法得到的是批的排序,因此必须转化为对应的位置矢量才能够参与微粒群算法的进一步进化搜索。因此按照如下方式实现转换:
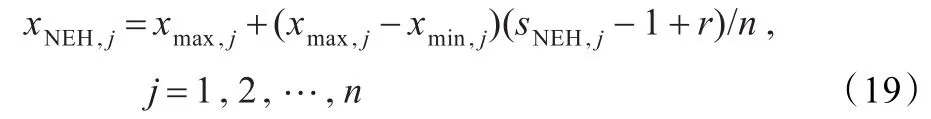
其中,xNEH,j为微粒在第j维的位置值;sNEH,j为通过NEH方法得到的解得第j维序号;xmax,j和xmin,j分别为连续空间上微粒位置的上界值和下界值,这里分别设置为4.0和-4.0;r代表0到1的一个随机数。
其余的微粒的位置矢量在一定连续区间内随机生成。
微粒的初始位置矢量采用如下方式随机生成:

其中xmin=0,xmax=4.0。
初始化微粒的速度矢量采用相似的方式,如下:

其中vmin=-4.0,vmax=4.0。微粒的速度被限制在特定的范围内,即[-4.0,4.0]。更新微粒速度的加速常数c1和c2,均设置为2.0。
微粒群算法的惯性权系数w的设置直接影响算法的收敛性,是调整全局和局部搜索能力的重要因素。较小的惯性权系数有利于精确局部搜索,使算法易于收敛,而较大的惯性权系数则有利于搜索跳出局部极小解,改善全局搜索。为了平衡算法的局部搜索和全局搜索能力,这里提出一种自适应惯性权系数AIWF的计算表达式,如下:

其中wmax和wmin分别为w的最大值和最小值,f为微粒当前的目标值函数,favg和fmin分别为微粒的平均值和最小目标值。
对依据上述方法生成的微粒(n为微粒的维度),根据ROV规则分别确定出各自的批序列的排序,并求得相应的目标函数值,即Makespan值。则每个微粒计算出的Makespan值即为各个微粒的初始最佳位置(pbest)对应的适应度函数值,而其中最小值对应的微粒的位置为初始的全局最佳位置(gbest)。
3.2.4 引入变邻域搜索改进gbest搜索机制
为了改进微粒群算法的局部搜索能力较差,容易陷入局部极小解的问题,这里在微粒每次更新中引入变邻域搜索算法,利用其无需设置参数,实现简单的特性,对微粒每次迭代更新时获得的gbest运用多个邻域结构进行搜索以获得新的gbest,从而提高了搜索的质量和效率。
对于微粒群算法,可进行的邻域搜索分为两种类型:一种是基于第t次迭代中第i个微粒的位置矢量的邻域搜索,另一种则是基于第t次迭代中第i个排序πi的第j个批πij的邻域搜索。本文将后一种邻域搜索技术引入每次的迭代更新中,采用了如下两种邻域结构:
(1)互换(interchange)
将第μ维和第η维的批互相交换位置产生新的批序列,图2(a)给出了将第1维所在的批与第4维所在的批执行interchange操作前后批的排序情况。
(2)插入(insert)
移除第μ维的批并将之插入第η维。图2(b)给出了将第1维所在的批与原第4维所在批执行insert操作前后的批的排序情况。

图2 变邻域搜索的两种邻域结构图
基于以上邻域搜索,变邻域搜索的算法流程如图3所示。

图3 VNS算法流程图
4 仿真实验
4.1 实验设计
为了测试算法的性能,以Melouk[13]等提出的方法生成随机测试实例。该方法考虑了问题在工件规模n、工件尺寸si和工件加工时间tj三个维度的变化。其中工件尺寸和工件加工时间均服从离散均匀分布。工件按工件数分类可得到J1,J2,J3,J4,J5,J6类问题,其工件数依次为20,50,100,200,300,500;根据工件尺寸的不同范围,问题可分为s1,s2,s3三类,尺寸区间依次为[2,4],[4,8],[1,10];根据工件加工时间所取的不同范围,问题可分为t1和t2两类,时间区间依次为[1,10]和[1,20]。综合上述三个维度可将具体问题表述为Jisjtk,i=1,2,…,6,j=1,2,3,k=1,2。例如:工件规模为20,工件尺寸服从[2,4]的离散均匀分布,工件加工时间服从[1,10]的离散均匀分布的实例,可表示为J1s1t10。实验中一共设计了36类子问题,假设每个批的最大容量均为10。这里所选的机器容量、工件加工时间以及工件尺寸代表了电子制造服务提供商的产品在环境应力筛选实验箱中的测试活动。


4.2 实验结果与分析
设微粒群算法的种群规模为9,批处理机的数量为3台,算法终止条件为迭代次数达到100次或者全体极值连续20次无改进。考虑到算例的随机性,采用200次实验所获得的结果的平均值进行比较。实验中分批阶段的算法均采用Palmer+BF获得初始分批,批的排序阶段测试的算法包括求解实例下界LB的算法、NEH启发式算法、标准的PSO算法以及改进的PSO算法(表中简称为PSOVNS),以上算法均在JDK 6.0环境下编程实现。测试结果如表2。

表2 各算法的测试结果

图4 算法性能表现图
在表1中,“平均”表示各算法200个算例Cmax的算术平均值;“比率”表示该平均值与算例平均下界的比率,该值越接近1则说明算法性能越好。表1的横轴依照不同的工件尺寸范围分为s1,s2,s3三类;纵轴按照工件规模将问题划为6类,即J1,J2,J3,J4,J5,J6,每一类工件规模又按照工件的加工时间分为t1和t2两类。如J1t1,表示工件规模为20且加工时间服从[2,4]离散均匀分布的情况。为了更清楚地比较各算法在以上的各个算例下的性能,给出算法性能表现图如图4。
由图4可知,在工件规模较小时,PSO算法与NEH算法相比没有什么优势,NEH算法的Cmax值优于标准PSO算法。但随着工件规模进一步增大,当规模大于200之后,PSO算法的性能逐渐超过NEH。而本文提出的PSOVNS算法由于在微粒初始化、参数设置以及gbest更新中引入不同的优化策略,求解结果在任何情况下均优于NEH启发式算法和标准PSO算法。
5 结论
流水车间批调度问题的分批以及批的排序均为NP难问题,而此类问题在现实中有着大量实例,对此问题的求解算法研究具有重要的现实意义。在该问题的分批阶段设计了基于Palmer+BF的分批策略,在批排序阶段提出了一种基于PSO算法的优化分配算法。在算法编码时,构造了基于ROV规则的排序方案;在微粒初始化时通过引入NEH启发式算法改进了初始解的生成质量,采用了一种自适应惯性权系数,并在更新gbest时引入了变邻域搜索来提高算法的局部搜索能力,避免了过早收敛的问题。仿真实验表明,本文算法对问题的求解是有效的,适于应用到生产实践中。
进一步的研究可从两方面进行:一是继续研究其他的智能优化算法在此问题的应用,如遗传算法、蚁群算法等,以及通过混合优化策略,结合不同算法的优点来提高求解质量;二是在分批阶段提出更好的分批策略,改进分批的质量,以及探讨首阶段分批与后阶段排序的关联性,以提高整体优化效果。
[1]Mirsanei H S.Flow shop scheduling with two batch processing machinesandnonidenticaljobsizes[J].IntJ AdvManuf Technol,2009,45:553-572.
[2]PurushothamanD,PraveenK.MinimizingMakespanona batch-processing machine with non-identical job sizes using genetic algorithms[J].Int J Production Economics,2006,103: 882-891.
[3]Alebachew D,Kudret D.Fuzzy scheduling of job orders in atwo-stageflowshopwithbatch-processingmachines[J]. International Journal of Approximate Reasoning,2009,50:117-137.
[4]Liao L M,Huang C J.Tabu search heuristic for two-machine flowshop with batch processing machines[J].Computers and Industrial Engineering,2011,60:426-432.
[5]Ali H.An improved mixed integer linear formulation and lower bounds for minimizing Makespan on a flow shop with batch processing machines[J].Int J Adv Manuf Technol,2009,40:582-594.
[6]梁艳春,吴春国.群智能优化算法理论与应用[M].北京:科学出版社,2009.
[7]王凌,刘波.微粒群优化与调度算法[M].北京:清华大学出版社,2008.
[8]Mladenovic N,Hansen P.Variable neighborhood search[J].Computer Ops Res,1997,24(11):1097-1100.
[9]Nawaz M,Enscore E,Ham I.A heuristic algorithm for the m-machine n-job flow shop sequencing problem[J].Omega,1983,11:11-95.
[10]Uzsoy R.Scheduling a single batch processing machine with nonidentical job sizes[J].International Journal of Production Research,1994,32(7):1615-1635.
[11]Palmer D.Sequencing jobs through a multi-stage process in the minimum total time-a quick method of obtaining a near optimum[J].Operation Research Quarterly,1965,16:101-107.
[12]Hall L A.Approximability of flow shop scheduling[C]// Proceedings of the 41st Annual Symposium on Foundations of Computer Science,Milwaukee,Wisconsin,2005:82-91.
[13]Melouk S,Damodaran P,Chang P Y.Minimizing Makespan for single machine batch processing with non-identical job sizes using simulated annealing[J].International Journal of Production Economics,2004,87(2):141-147.
ZHU Qi,CHEN Chengdong,CHEN Huaping
School of Management,University of Science and Technology of China,Hefei 230026,China
An approach based on swarm intelligence is presented to solve the problem of scheduling tasks on flow-shop with batch processing machines.According to the characteristics of the problem under study,a method based on Palmer and Best Fit heuristic algorithm is developed to form batches.Moreover,an improved Particle Swarm Optimization(PSO)algorithm is presented to sequence the obtained batches.In PSO,the NEH heuristic is employed to improve the quality of the initial population. In order to enhance the search capabilities of the proposed algorithm,a variable neighborhood searching is performed for each iteration before the global best position is updated.The experimental results show that the proposed algorithm has a better effectiveness than the standard PSO algorithm and the NEH heuristic.
flow-shop;batch processing machines;Particle Swarm Optimization(PSO);variable neighborhood search
针对流水车间批调度问题,提出一种基于群智能算法的求解思路。结合问题具体特点,给出工件集合的分批策略,设计了将Palmer和Best Fit(BF)分批规则相结合的分批方法;在批排序阶段,提出了一种改进的微粒群算法;在粒子初始生成阶段,通过引入NEH启发式算法改进了粒子的初始化质量;在全局最佳位置更新前,通过变邻域搜索优化了算法的局部搜索能力,避免了算法陷入局部最优。仿真实验表明,改进后的算法优于传统的微粒群算法和NEH启发式算法。
流水车间;批处理机;微粒群算法;变邻域搜索
A
TP301
10.3778/j.issn.1002-8331.1111-0048
ZHU Qi,CHEN Chengdong,CHEN Huaping.Scheduling flow-shop problem with batch processing machines and non-identical job size.Computer Engineering and Applications,2013,49(13):221-227.
国家自然科学基金(No.70821001,No.71171184)。
朱颀(1983—),男,硕士研究生,研究领域:生产调度与智能算法;陈成栋(1985—),男,硕士研究生,研究领域:生产调度与智能算法;陈华平(1965—),博士生导师,中国科学技术大学计算机科学与技术学院执行院长,研究领域:网络计算,高性能计算,智能计算及其应用。
2011-11-10
2012-01-19
1002-8331(2013)13-0221-07
CNKI出版日期:2012-04-25http://www.cnki.net/kcms/detail/11.2127.TP.20120425.1723.093.html

