基于粒子群的改进模糊聚类图像分割算法

刘欢，肖根福

1.井冈山大学 电子与信息工程学院，江西 吉安 343009 2.井冈山大学 机电学院，江西 吉安 343009

基于粒子群的改进模糊聚类图像分割算法

刘欢1，肖根福2

1.井冈山大学 电子与信息工程学院，江西 吉安 343009 2.井冈山大学 机电学院，江西 吉安 343009

1 引言

图像分割是图像分析和模式识别需要解决的首要问题和基本问题，也是图像处理和计算机视觉的经典难题之一，它决定了图像的最终分析质量和模式识别的判别结果[1]。基于模糊理论的分割算法，特别是作为软分类方法的模糊C均值（FCM）算法[2]可以较好地解决图像信息的不确定性及多解性[3]，已经被成功地应用到图像分割中。标准的FCM聚类算法没有顾及像素的空间信息，对噪声比较敏感；其次，FCM待聚类点的坐标值与目标函数都是离散量，迭代容易陷入局部极值，对初始值敏感，迭代过程中计算量太大，使聚类速度和性能都受到影响。为提高FCM算法的抗噪性能，近年来，许多研究提出了采用新的距离度量方法取代欧氏距离作为差异性的度量标准。文献[4]提出了一种基于空间信息的可能性模糊C均值聚类算法，在一定程度上克服了FCM对噪声的敏感性；文献[5-7]把核聚类算法与FCM结合，用内核诱导距离来代替传统FCM中采用的欧氏距离，从而把给定空间的非线性距离转化为高维空间的线性距离；文献[8]以FCM聚类中心建立网络图，通过网络图扩展移动求解能量函数最上值，实现图像分割。这些算法依然存在对初始聚类中心数据较为敏感，运算速度慢等缺点。

微粒群优化算法（PSO algorithm）[9-10]是Kennedy和Eberhart于1995年提出的一种新兴的基于群体智能启发式全局搜索算法，具有易理解、易实现以及全局搜索能力强等特点。文献[11]采用基于混沌粒子群的模糊C均值聚类算法，利用粒子群算法强大的全局寻优能力避免算法收敛于局部极值，但并没解决FCM对噪声敏感等缺陷。

本文结合PSO提出了一种新的模糊聚类图像分割方法：PSO_TDFCM。该方法利用微粒群较强的搜索能力搜索聚类中心，用像素点的灰度值和该像素点的空间邻域单元熵的二维距离度量代替欧式距离，各像素领域单元熵体现了图像局部单元的统计特征，不仅描述了图像的全局特性也反映了图像的空间分布特性；同时在目标函数中加入邻域距离约束项。与标准FCM图像分割算法相比，本文的图像分割算法抗噪能力更强，对初始聚类中心不敏感，收敛速度更快，分割效果更佳。

2 TDFCM算法

2.1 TDFCM算法原理

任何图像都可以定义为由一系列像素点组成的二维数组，大小为M×N的矩形框架S={(i，j),1≤i≤M，1≤j≤N}，坐标系由(i，j)确定，位置s=(si，sj)上的像素灰度值用xs表示。

TDFCM算法的基本思想是将普通FCM算法（一维FCM）中的像素值用（灰度值、邻域单元熵）对代替，而聚类中心由（中心灰度值、中心邻域单元熵）对代替；同时考虑到像素间的空间约束关系，加入邻域距离约束项，它的目标函数为：

式（1）中，Xk=[xk，exk]T，Mi=[mi，emi]T为矢量；xk为某一点的像素灰度值，exk为像素xk一定窗口单元Nk内像素的熵；mi为图像像素的聚类中心，emi为像素单元熵的聚类中心；为点xk的邻域Nk中的像素的均值（不包括本身）到聚类中心mi的距离；β是正则化系数，其大小控制着后一项对前一项的相对影响。式（1）中的距离度量如式（2）所示，距离约束项中的如式（3）所示，单元熵计算如式（4）所示：

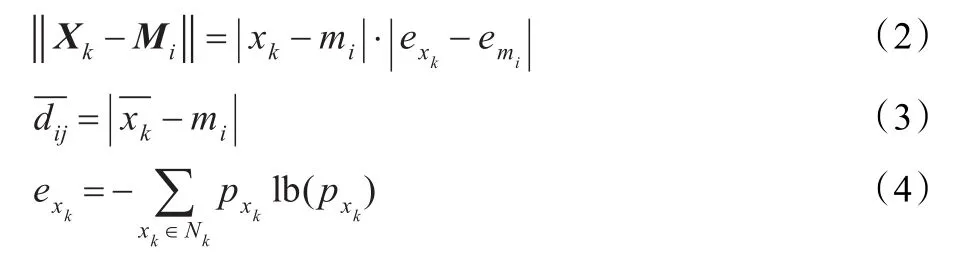
2.2 TDFCM算法实现

算法实现的具体步骤为：

步骤1确定聚类的数目c，设定聚类中心更新的终止条件ε=0.001。

步骤2根据二维Xk=[xk，exk]T统计初始化聚类中心Mi=[mi，emi]T。

步骤3由式（5）更新隶属度矩阵。

步骤4由式（6）、（7）更新聚类中心。

步骤5计算更新前、后聚类中心的改变量为用下式计算：

步骤6采用最大隶属度法去模糊化。

2.3 β参数的选取

β是正则化系数，其大小控制着后一项（邻域信息）对前一项的相对影响。若β太小，则平滑效果不明显，若β太大，则可能导致最后分割的错误。现给出一种β的选取办法，先使用标准FCM算法对图像进行分割，得到最佳的划分矩阵U和目标函数JFCM值，再计算该划分矩阵U对应的下述函数值，式中：NR表示邻域的大小。

3 微粒群优化算法

粒子群优化算法的基本思想源于模拟鸟群飞行觅食的行为，通过鸟之间的集体协作使群体达到最优。粒子群算法初始化为一组随机粒子，然后通过迭代寻找最优解。粒子追随两个最优值来更新自己，一个是粒子迄今为止寻找到的最优值，叫做个体极值（pBest）；另外一个是整个粒子群迄今为止寻找到的最优值，叫做全局极值（gBest）。粒子用以下公式更新自己：

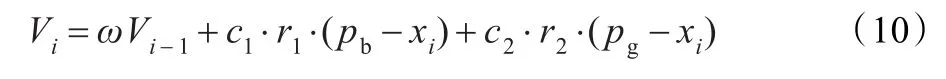
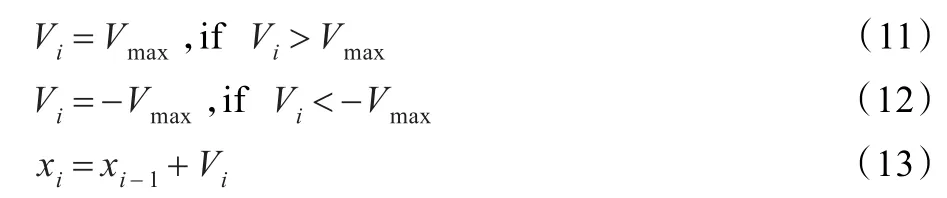
其中，Vi为当代粒子移动速度；Vi-1为前一代粒子移动速度；r1、r2为介于[0，1]之间随机数；c1、c2为学习因子，一般取2；xi为当代粒子位置；xi-1为前一代粒子位置；pb为个体最优位置，pg为全局最优位置；w为惯性因子。

搜索时，微粒的速度被最大速度vmax所限制。微粒的最大速度决定了解空间的搜索精度，对vmax进行动态调整可以使算法具有较好的自适应寻优效果。

4 PSO_TDFCM算法的策略和步骤

本文在对传统FCM图像分割算法存在的问题进行深入分析和研究的基础上，提出了一种带邻域约束项的融入空间信息的改进图像分割算法TDFCM。由于该算法存在对初始聚类中心敏感，计算量大等问题，因此又提出了基于微粒群优化的PSO_TDFCM分割方法，将微粒群算法与TDFCM相结合。该算法的基本思想：整个算法分成二个阶段。第一阶段利用微粒群算法具有全局寻优能力，获得数个最佳的峰值点；第二阶段将第一阶段获得的峰值点作为本阶段图像分割的初始类中心，利用TDFCM对图像进行分类，实现图像分割。

PSO_TDFCM图像分割算法步骤如下所示。

第一阶段：

步骤1用TDFCM算法得到聚类中心作为微粒群算法的初始值，设微粒群规模N=10，误差ε=0.001。

步骤2初始化微粒位置、速度、适应值。

步骤3用式（10）、（11）、（12）修改微粒速度，用式（13）修改微粒的位置。

步骤4.1对于每个微粒，将其当前适应值与其历史最优位置适应值比较，若当前适应值较大，则更新历史最优适应值，将当前位置作为历史最优好位置；

步骤4.2当前所有粒子中最优位置的适应值与群历史最优位置适应值比较，若当前所有粒子最优位置的适应值较大，则更新群历史最优适应值，将当前所有粒子中最优位置作为群历史最优好位置。

步骤5判断循环条件是否成立，如果ε＞0.001则转步骤3；否则步骤6。

步骤6由此获得的最佳粒子位置作为第二阶段的初始类中心，转第二阶段。

第二阶段：

步骤1由第一阶段得到结果初始类中心（中心灰度值，中心邻域单元熵）对gBest。

步骤2由式（5）计算隶属度矩阵μi(xk)。

步骤3用式（6）、（7）计算分类中心矩阵mi，emi。

步骤4判断是否停止迭代计算，如果则转步骤2；否则转步骤5。

步骤5根据图像中各像素对类中心的隶属度对图像去模糊化，实现图像分割。

5 实验结果

以Lena图像为例，图1（a）为标准Lena图像，图2（a）为叠加了2%的椒盐噪声的Lena图像。分别应用三种不同的分割算法，即标准的FCM算法、本文的TDFCM算法和基于PSO_TDFCM的算法进行图像分割实验，并对三种方法获得的结果进行比较。本文使用PSOT粒子群优化工具箱里的标准PSO算法，在MATLAB2012a中进行优化实验。PSO算法的参数采用默认值：加速系数c1=2.0，c2=2.0，最小惯性权值ω=0.4，最大惯性权值ω=0.9。综合粒子维数、算法的精度、稳定性和运行时间等多个因素，考虑选择粒子群规模为10，误差精度ε=0.001，算法最大迭代次数30，粒子速度限制在[-1，1]之间；图像分割算法中，定义在3×3大小的图像窗口中计算对应点的熵作为该点的邻域单元熵，聚类数为6。实验结果如图1（b）、（c）、（d），分别为FCM、TDFCM、PSO_TDFCM算法对原图的分割效果图；如图2（b）、（c）、（d）分别为FCM、TDFCM、PSO_TDFCM算法对Lena加2%椒盐噪声图的分割效果图。

图1 Lena原图及分割效果图

图2 Lena噪声图及分割效果图

从分割结果对比图可以看出，TDFCM算法的抗噪能力明显好于FCM算法，而PSO_TDFCM算法较TDFCM算法也有一定的改善。

表1给出了描述以上三种算法的图像分割结果的定量指标，其Time为图像分割时间，Vpc为划分系数，Vpe划分熵；划分系数越大，划分越熵小，表明分割效果越好。从表1中可以看出，FCM算法时间最少，TDFCM算法由于是二维运算分割时间比FCM算法长，PSO_TDFCM算法先利用PSO算法获得了最优聚类中心，分割时间（不包括PSO算法运行时间）比TDFCM算法短，但还是比FCM算法要长；从划分系数来看，PSO_TDFCM算法最大，其次是TDFCM算法，最小的是FCM算法；从划分熵来看，PSO_TDFCM算法最小，其次是TDFCM算法，最大的是FCM算法。这表明PSO_TDFCM算法分割效果最佳，其次是TDFCM算法，FCM算法最差。

表1 Lena标准图和2%椒盐噪声图的FCM、TDFCM、PSO_TDFCM算法定量指标比较

表2给出了Lena标准图和噪声图中PSO_TDFCM和TDFCM算法分别与FCM算法相比，划分系数和划分熵的变化程度。PSO_TDFCM、TDFCM算法比FCM算法的划分系数都有一定程度的增加，划分熵都有一定程度的下降，尤其在噪声图像中PSO_TDFCM算法划分系数的增加幅度要大于TDFCM算法的增加幅度，划分熵的下降幅度也大于TDFCM算法的下降幅度。

表2 Lena标准图和2%椒盐噪声图TDFCM、PSO_TDFCM算法分别与FCM算法指标变化幅度的比较（%）

表3给出了三种算法各自在Lena标准图和噪声图间的变化程度。PSO_TDFCM算法分割时间的增加幅度最小，其次是TDFCM算法，最大的是FCM算法；对划分系数的下降幅度和划分熵的增加幅度，PSO_TDFCM算法都是最小，其次是TDFCM算法，最大的FCM算法。

综合评价PSO_TDFCM算法的聚类效果比TDFCM和FCM算法好，取得了较满意的分割效率，尤其是对噪声图像分割时表现出来了明显的优势。

表3 三个算法在Lena标准图和2%椒盐噪声图间指标变化幅度的比较（%）

6 结论

本文将粒子群算法与融入空间邻域灰度熵、带有距离约束项的模糊聚类图像分割算法相结合，提出了一种新的算法。在距离度量中引入邻域单元熵用二维距离代替传统的一维距离度量，具有良好的收敛性，分割更准确；在目标函数中加入约束项有效地解决了标准FCM对噪声敏感的缺点；利用粒子群算法的全局寻优能力，改善了标准FCM对初始聚类中心敏感，提高了分割速度与精度。实验结果表明，与其他算法相比，本文算法分割效果较理想，尤其对有噪声图像的分割表现出了明显的优势，算法具有广泛的实用价值。

[1]Cheng H D，Jiang X H，Sun Y，et al.Color image segmentation：advances and prospects[J].Pattern Recognition，2001，34：2259.

[2]Bezdek J C.Pattern recognition with fuzzy objective function algorithms[M].New York：Plenum Press，1981.

[3]王适，蒋璐璐，王宝成.改进的模糊C均值聚类遥感图像分割方法[J].计算机应用，2010，30（S2）：54-57.

[4]张一行，王霞，方世明.基于空间信息的可能性模糊C均值聚类遥感图像分割[J].计算机应用，2011，31（11）：3004-3007.

[5]Soddu C.Recreating the city’s identity with a morphogenetic urban design[C]//Proceeding of the 17th International Conference on Making Cities Livable，Freibure-in-Bresfau，1995：5-9.

[6]刘弘，刘希玉.支持外观造型创新设计的进化计算方法[J].计算机辅助设计与图形学学报，2006，18（1）：101-107.

[7]俞国燕，何真，郑时雄.基于人机一体的混合智能创新设计[J].计算机工程与应用，2003，39（7）：43-45.

[8]王晓飞，郭敏.结合模糊C均值聚类与图割的图像分割方法[J].计算机应用，2009，29（7）：1918-1920.

[9]刘金洋，郭茂祖，邓超.基于雁群启示的粒子群优化算法[J].计算机科学，2006，33（11）：166-168.

[10]Kennedy J，Eberhart R C.Particle swarm optimization[C]// Proc of the IEEE International Conference on Neural Networks，1995：1942-1948.

[11]左浩，李雯.混沌粒子群与模糊聚类在图像分割中的应用[J].计算机工程与应用，2012，48（2）：194-196.

LIU Huan1,XIAO Genfu2

1.Collgeg of Electronic and Information Engineering,Jinggangshan University,Ji’an,Jiangxi 343009,China
2.College of Machinery and Electrons,Jinggangshan University,Ji’an,Jiangxi 343009,China

In improved fuzzy clustering image segmentation method based on Particle Swarm Optimization（PSO_TDFCM）, the clustering centers searched by particle swarm are taken as image segmentation clustering initializations,which overcomes the sensitive to the clustering center initializations for Fuzzy C-Means（FCM）algorithm as well as improves the speed of FCM algorithm greatly.Meanwhile,on the one hand,the new idea taken into account the great correlation between the spatial site information of a pixel and it’s neighboring pixels,consequently,the neighboring penalized function is added in the objective function；on the other hand,it suggests to update the clustering centers at the two-dimension directions,from which the new objective function combines cell entropy.The results of comparative experiments demonstrate that this approach is an effective fuzzy clustering image segmentation algorithm,which can make a marked improvement in the speed of fuzzy clustering as well as insensitive to the initial clustering patters and robust to the noise.

particle swarm;Fuzzy C-Means clustering（FCM）;image segmentation;neighboring information;cell entropy

基于粒子群优化的改进模糊聚类图像分割算法将微粒群搜索聚类中心作为图像分割的聚类初值，克服了FCM分割算法对聚类中心初值敏感的缺点，大幅提高了图像分割算法的计算速度。改进的模糊聚类图像分割算法，一方面考虑到像素的空间位置信息和相互邻域之间像素有很大的相关性，在目标函数中引入邻域惩罚函数；另一方面提出聚类在二维方向上进行更新的思想，建立了包含邻域单元熵的新聚类目标函数。实验结果表明，该方法可以使模糊聚类的速度得到明显提高，对初始聚类中心不敏感，抗噪能力强，是一种有效的模糊聚类图像分割方法。

粒子群；模糊C均值聚类；图像分割；邻域信息；单元熵

A

TP391.41

10.3778/j.issn.1002-8331.1208-0074

LIU Huan,XIAO Genfu.Improved fuzzy clustering image segmentation algorithm based on particle swarm optimization.Computer Engineering and Applications,2013,49（13）：152-155.

井冈山大学校级课题（No.JZ10011）。

刘欢（1981—），女，博士生，讲师，主要研究领域为图形图像处理，模式识别与智能系统；肖根福（1980—），男，博士生，讲师，主要研究领域为智能控制，数值计算。E-mail：liuhuan816618@163.com

2012-08-06

2012-09-27

1002-8331（2013）13-0152-04

CNKI出版日期：2012-11-21http://www.cnki.net/kcms/detail/11.2127.TP.20121121.1100.014.html