基于邻域场拉普拉斯混合模型图像分割的研究

罗雷，王士同

江南大学 数字媒体学院，江苏 无锡 214122

基于邻域场拉普拉斯混合模型图像分割的研究

罗雷，王士同

江南大学 数字媒体学院，江苏 无锡 214122

1 引言

在影像识别和图像处理中图像分割技术已经得到广泛应用，好的分割结果能够为信息判断提供有力的依据。然而图像很容易受到噪声的影响，这就给图像分割带来一定的难度。为了解决这个问题，一些方法相继得到应用，如模糊聚类[1-2]、直方图[3]、人工神经网络[4]以及有限混合模型[5]。其中有限混合模型由于其复杂度仅与待求解的问题有关，与样本大小无关，并且兼具有参估计和无参估计的特点得到了广泛应用[6-7]，另外它还是一种半参数估计方法，并不局限于某一特定方法。高斯混合模型是一种常见的有限混合模型，它凭借其形式简单、计算方便等特点，已成为应用比较普遍的有限混合模型。相比较标准高斯混合模型（GMM）中像素点有共同的先验概率πj，新型高斯混合模型（GMM）[8]先验概率πij取决于像素点邻域的相互作用，每个像素点有自己独立先验概率πij。然而实际中得到的数据大多具有非线性、非高斯特性，而高斯分布拟合能力有限，导致其不能完全、准确、有效地描述这些复杂数据。研究发现，在工程应用中，噪声模型概率密度分布往往具有比较厚的尾部统计特性[9]。如合成孔径雷达图像中，海杂波的尖峰幅度分布情况，都呈现出很多幅度较大的噪声，此时的噪声就是重尾噪声，而不再是高斯噪声。对于重尾噪声的研究和应用并不局限于上述领域中，也有必要将其引入到图像分割研究中。相较于高斯分布，拉普拉斯分布是一种重尾分布[10]，它具有尖峰后尾的统计特性，因而拉普拉斯模型比高斯模型更强大，并且在图像分割方面更有效。然而其现有的模型中，先验概率πj并不取决于独立的像素点，它对于所有的像素点都是同一个值，没有考虑到像素的空间邻域性。另外，现有的拉普拉斯模型在估计参数时，一般都效仿传统的高斯模型采用EM算法[11]，而这种方法增加了算法的复杂性。

基于上述考虑，本文提出了一种新的拉普拉斯混合模型。该方法将新型高斯混合模型考虑到的像素点空间邻域关系引入到标准拉普拉斯混合模型。本文方法与上述方法不同之处主要体现在几个方面：第一，相较于高斯分布本文采用的拉普拉斯分布具有尖峰后尾的统计特性，在处理噪声尤其是重尾噪声时更加平滑；第二，相比较标准拉普拉斯模型，本模型的不同之处在于每个像素点的先验概率是不同的，它取决于这个像素点及它的相邻像素点；第三，由于考虑了相邻像素点间的联系，本模型提取这些信息后处理噪声效果更好。另外，在估计参数时，本方法并没有采用EM算法，而是使用梯度下降法求解负似然对数最小值。实验研究了本文方法与目前存在的拉普拉斯混合模型与高斯混合模型在图像分割方面的应用，探讨了基于邻域场拉普拉斯混合模型在处理图像分割方面的优势。

2 基于有限混合模型图像分割研究现状

有限混合模型在图像分割中的应用已经相当广泛，许多方法都取得了不错的效果，尤其是高斯混合模型。图像分割中习惯性加入的噪声往往是高斯噪声，这样促进了高斯混合模型的发展。然而现实中，遇到的往往是非高斯、非线性噪声。下面将介绍常见的重尾噪声、具有重尾特性的拉普拉斯混合模型以及处理高斯噪声效果较好的新型高斯混合模型。

2.1 重尾噪声

在研究含重尾噪声的图像分割前，首先了解常见的重尾噪声[12-13]。现实中常见的噪声主要有高斯噪声、椒盐噪声、乘性噪声、重尾噪声等，其中重尾噪声主要有混合高斯噪声、拉普拉斯噪声、柯西噪声、Erland噪声、负指数噪声等。它们的概率密度函数详细表述如下：

（1）混合高斯分布

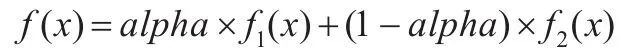
其中，f1(x)是x～N(μ1,σ1)的概率密度函数，f2(x)是x～N(μ2,σ2)的概率密度函数，则称f(x)为混合高斯分布。一般μ1=μ2，σ1≤σ2，0≤alpha≤1。

（2）拉普拉斯（Laplace）分布

其中，均值为μ，协方差为2σ2。

（3）柯西（Cauchy）分布

其中，x0是位置参数，γ＞0是尺度参数，均值不存在。

（4）Erlang分布

上述密度函数相较高斯分布来说更加复杂，导致高斯分布在拟合它们的时候不甚理想。下面介绍标准拉普拉斯混合模型以及新型高斯混合模型在图像分割方面的应用。

2.2 标准拉普拉斯混合模型（LMM）

设xi，i=1，2，…，N，表示一幅图像的第i个像素点，xi满足独立分布特性，另设图像分可为K个标签，Ωj表示第j个标签，j=1，2，…，K。为了将图像的N个像素点划分为K个标签，拉谱拉斯混合模型[14]假定每个像素点xi分别服从每个拉普拉斯分布，且独立于各个标签Ωj。像素点xi在第j个标签出现的概率密度函数表示为：

每个拉普拉斯分布p(xi|Ωj)为混合模型的一个部件，概率密度函数为：

其中，拉普拉斯分布均值为μj，协方差为2b2j。根据式（1）可以得到似然对数估计[15]：

为了得到式（3）中的最大似然函数，定义参数集θ=(μj，bj，πj)，j=1，2，…，K，许多方法都可以通过调整这些参数达到目的。根据优化参数后的拉普拉斯模型，以及式（4）对像素点进行标签标记。

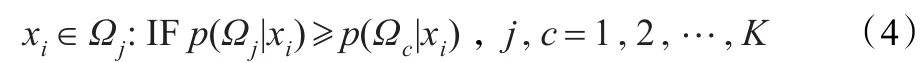
其中，后验概率p(Ωj|xi)由贝叶斯（Bayes’）公式得到：

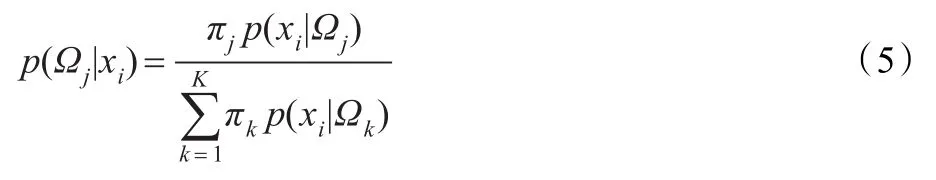
2.3 新型高斯混合模型（GMM）

新型高斯混合模型在标准高斯模型（GMM）的基础上考虑了像素点的空间邻距离。

观测值xi的密度函数设为：

同理将πij代入式（3）中，可以得到新的似然对数函数：

考虑到对数函数是非负递增函数，根据经验求解负似然对数函数相对较为方便。

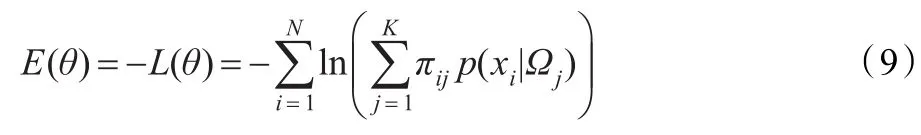
求解负似然对数的最小值，相当于求解下面函数式的最小值[8，16]：

式中的ε可以看做是一个误差函数，因此求解式（8）中L的最大值相当于求解ε的最小值。求解ε的最小值也就相当于对参数集进行优化，在下面的内容中将会介绍。将优化后的参数代入到式（7）得到后验概率，再利用式（4）得到最终的标记结果。

3 基于邻域场拉普拉斯混合模型（LMM）

上文提到现实中的噪声往往是非高斯非线性的，高斯分布由于其本身拟合能力有限在处理这方面问题时效果往往不理想，尤其是在处理重尾噪声过程中。如图1所示，拉普拉斯分布与高斯分布在选取相同参数情况下，前者较后者呈现尖峰重尾特性，因而拟合能力更好。标准拉普拉斯混合模型中，虽然拉普拉斯分布具有重尾特性但是模型并没有考虑到像素点的空间关系，这样的模型处理重尾噪声时效果也不理想。

图1 拉普拉斯分布与高斯分布密度函数

基于上述考虑，设想如果能将高斯混合模型中考虑到的像素空间关系引进到重尾分布模型中，那么这种新方法在处理重尾噪声图像分割时效果将会提高。

根据上面的分析给出了一种新型拉普拉斯混合模型，该模型比GMM有更好的拟合能力，与标准拉普拉斯模型最大的不同在于后验概率πij具有独特性，它不仅依据每个像素点的个性还充分考虑了像素点的空间关系。

3.1 基于空间关系的先验概率πij

设一幅灰度图像由U×V个像素点构成，为了叙述方便，设x(u，v)表示图像的第i个像素点，这里i=U() u-1+v，u=1，2，…，U且v=1，2，…，V。如前文所述，本文方法的最大不同在于考虑了像素点的独立性，以及空间领域性，主要体现在：像素点的空间联系采用3×3窗口形式如图2所示，这样像素点之间的相似性以及相互的影响就得到了充分的考虑。

图2 相邻像素点3×3窗口

定义1第i个窗口领域点的像素集表示为：

其中cj和dj，j=1，2，…，K，是优化后的参数，在后面将会介绍优化方法。将式（12）代入式（11），可以得到考虑邻距离之后第i个窗口隶属于Ωj的平均隶属度：

下面将这种考虑到空间关系的方法应用到先验概率πij，这样就可以得到图像中每个像素点隶属于Ωj的先验概率：

3.2 参数优化

上文主要讨论了像素点xi属于Ωj的概率估计问题。而要得到泛化后的结果就需要对参数集θ=(μj，bj，cj，dj)，j=1，2，…，K进行优化，也就是最小化式（10）中的ε，这部分将讨论这个问题。相对一般的优化算法采用EM算法，本文采用梯度下降法。

误差函数式（10）可以改写为：

具体算法描述：

（1）使用K-mean方法初始化μj、bj，令cj=μj，dj=bj，完成θold的初始化。

其中，pold(xi|Ωj)和根据式（2）与式（14）得到。

（3）运用梯度下降法[16]更新参数集θ=(μj，bj，cj，dj)，新的参数集θnew为：

（4）检查E(θ)和参数是否收敛，如果都没有，令θold=θnew，返回第（2）步。

（5）将优化后的结果代入式（4），得到最终标记结果。

4 模拟实验及分析

实验给出了本文算法与K-mean、FCM（Fuzzy C-Means）、标准LMM和GMM等算法图像分割效果的比较。实验都是基于Window平台Matlab软件完成的，实验结果均是各算法收敛后得到的数值。考察实验结果的优良，采用的是错误率MCR，它等于分割错误的像素点比上总的像素点。限于篇幅限制，本文主要比较加入混合高斯噪声和拉普拉斯噪声的图像分割效果。

4.1 人工合成图像

在第一组实验中加入的噪声是混合高斯噪声，实验使用的是一张合成图像，由128×128个像素点构成，共有四种灰度值[0.25，0.50，0.75，1.00]。图3（a）为原始图像，图3（b）为加混合高斯噪声图像，参数值为alpha=0.02，均值μ1=μ2，协方差σ1=0.05，σ2=0.07；图3（c）和（d）分别为K-mean和FCM分割结果，从图中很容易看出，分割结果非常糟糕，其错误率分别达到7.61%和8.51%（如表1）；图3（e）和（f）是标准LMM和GMM算法分割的结果；本文算法的分割结果如图3（g），其分割效果相对于前面的算法要好得多，错误率已经降低到了1.63%。

图3 图像加混合高斯噪声分割结果

表1 图像加混合高斯噪声分割结果比较(MCR)（%）

第二组实验比较的是各算法对于加入拉普拉斯噪声后图像的分割效果。图像同样是人工合成，共128×128个像素点构成，灰度等级则达到了五类，分别是0.2，0.4，0.6，0.8，1.0。图4（a）是原图像，图4（b）为加入拉普拉斯噪声后的图像，其中参数为a=0，σ=0.04。表2是拉普拉斯噪声下，a=0，σ不同值时，几种算法的MCR。容易看出，本文算法准确性要比其他算法好，另外本文算法与GMM比较，由于拉普拉斯对尖峰拖尾的情况有更好的适应性，故本文算法比GMM有更好的鲁棒性。

图4 图像加拉普拉斯噪声分割结果

表2 图像加拉普拉斯噪声分割结果比较(MCR)（%）

4.2 模拟人脑图像

第三组实验使用的图像来自Brainweb网站，每组图像由128像素×128像素构成，T1加权，层厚1 mm。图5（a）是真实分割效果图，设分割为四类，分别是白质、灰质、脑髓液和背景。图5（b）加入的是混合高斯噪声，其中均值均为0，σ1=0.01，σ2=0.02，alpha=0.02，可以看到加入噪声后图像已经相当模糊。通过图像间的对比，可以直观地看到本文方法相较其他方法效果更好；另外根据表3（均值均为0，σ1=0，01，alpha=0.02，σ2变化）提供的数据，进一步证明了直观的判断。

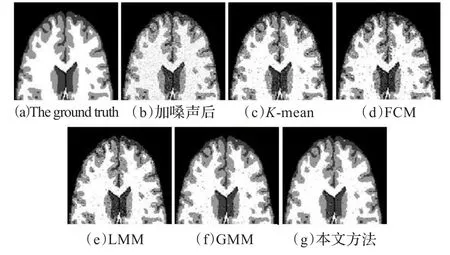
图5 图像加混合高斯噪声分割结果

表3 图像加混合高斯噪声分割结果比较(MCR)（%）

第四组实验使用的原始图像与第三组是一致的（如图6），为了证明本文方法不仅仅适用于混合高斯噪声，在同样的图像中加入了拉普拉斯噪声。图6（b）加入的拉普拉斯噪声均值为0，σ=0.06。图6和表4证实了本文方法在处理拉普拉斯噪声时，比K-mean、FCM和LMM算法要好得多。同样，相比高斯分布，拉普拉斯分布的重尾特性在有限混合模型处理拉普拉斯噪声时，体现出了优势。

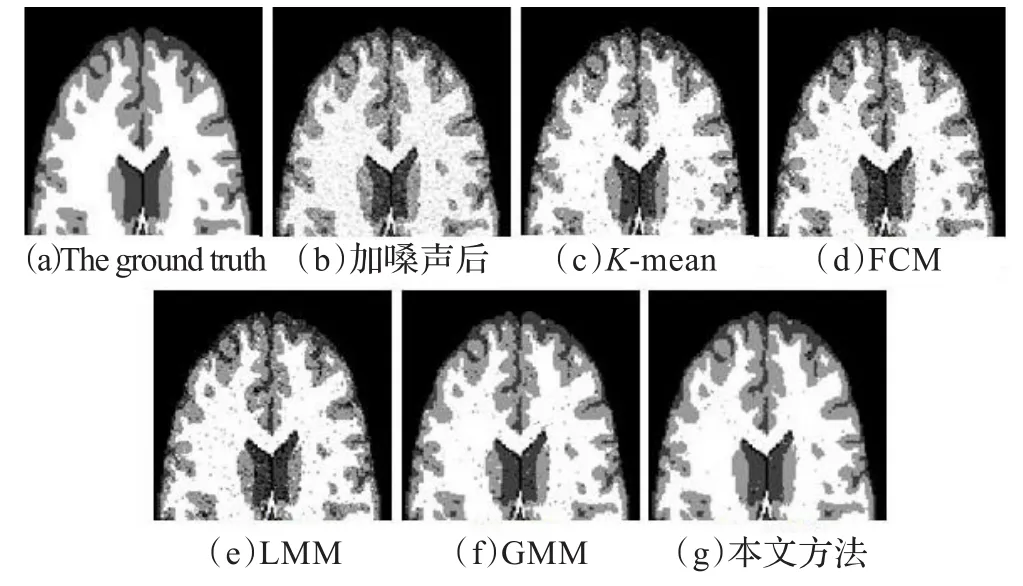
图6 图像加拉普拉斯噪声分割结果

表4 图像加拉普拉斯噪声分割结果比较(MCR)（%）

5 结束语

本文提出了一种新的模型用于灰度图像分割，它在标准拉普拉斯混合模型基础上融合了相邻像素点的空间关系。前文提到过，每个像素点的先验分布πij都是不同的，它取决于像素点和它的周围像素点以及相关的参数，这也正是本文方法和标准拉普拉斯模型的不同之处。与GMM算法相比，由于拉普拉斯分布具有尖峰后尾的统计特性，在处理重尾噪声时，基于邻域场的拉普拉斯混合模型无论是鲁棒性还是精确度都相对要好。

[1]Kim S，Kang M.Multiple-region seg-mentation without supervision by adaptive global maximum clustering[J].IEEE Transactions on Image Processing，2012，21（4）：1600-1612.

[2]张扬，王士同，韩斌.基于改进模糊聚类算法鲁棒的图像分割[J].中国图象图形学报，2008，13（5）：911-917.

[3]Goncalves H，Goncalves J A，Corte Real L.HAIRS：a method forautomaticimageregistrationthroughhisto-gram-based image segmentation[J].Transactions on Image Processing，2011，20（3）：776-789.

[4]Bors A，Pitas G I.Optical flow estimation and moving object segmentation based on median radial basis function network[J]. IEEE Transactions on Image Processing，1998，7（5）：693-702.

[5]Mclachlan G J，Peel D.Finite mixture models[M].New York：Wiley，2000.

[6]Ji Z，Xia Y，Sun Q，et al.Fuzzy local Gaussian mixture model for brain MR image segmentation[J].IEEE Transactions on Information Technology in Biomedicine，2012，16（3）：339-347.

[7]Singh R，Pal B C，Jabr R A.Statistical representation of distributionsystemloadsusinggaussionmixturemodel[J]. IEEE Trans on Power Systems，2010，25（1）：29-37.

[8]Nguyen T M，Wu Q M.Gaussian-mixture-model-based spatial neighborhoodrelation-shipsforpixellabelingproblem[J]. IEEE Transactions on Systems Man and Cybernetics：Part B Cybernetics，2012，42（1）：193-202.

[9]Mukherjee A，Sengupta A.Estimating the probability density function of a non-stationary non-Gaussian noise[J].IEEE Transactions on Industrial Electronics，2010，57（4）：1429-1435.

[10]Wang X，Zhang X.A new Laplacian mixture conditional random field for image labeling[C]//Proceedings of the IEEE International conference on Acoustics Speech and Signal Processing（ICASSP），2010：2118-2121.

[11]Tian G，Xia Y，Zhang Y，et al.Hybrid genetic and variational expectation-maximization algorithm for Gaussian-mixture-modelbased brain MR image segmentation[J].IEEE Transactions on Information Technology in Biomedicine，2011，15（3）：373-380.

[12]王桥.数字图像处理[M].北京：科学出版社，2009：21-30.

[13]张如艳，王士同.基于重尾噪声分布特性的多分类人脸识别方法[J].电子与信息学报，2012，34（12）：523-528.

[14]Amin T，Guan L.Application of laplacian mixture model to image and video retrieval[J].IEEE Transactions on Multimedia，2007，9（7）：1416-1429.

[15]Bishop C M.Pattern recognition and machine learning[M].New York：Springer-Verlag，2006.

[16]Lange K，Fessler J A.Globally convergent algorithms for maximum a posteriori transmission tomography[J].IEEE Transactions on Image Processing，1995，4（10）：1430-1438.

LUO Lei,WANG Shitong

School of Digital Media,Jiangnan University,Wuxi,Jiangsu 214122,China

Finite mixture model under Laplacian distribution is proposed in order to solve the problem that image segmentation based on Gaussian Mixture Model（GMM）failing to settle tailing situation with heavy-tailed noise,besides,unlike the standard Laplacian Mixture model（LMM）where pixels themselves are considered independent of each other,the proposed method incorporates the spatial neighborhood relationship of pixels into the standard LMM.In order to estimate model parameters from observations and instead of utilizing an expectation-maximization algorithm,the gradient method is adopted.The experimental results demonstrate the robustness,accuracy,and effectiveness of the method in comparison with the standard LMM and GMM.

Laplacian Mixture Model（LMM）;image segmentation;heavy-tailed noise;spatial neighborhood relationship

针对高斯混合模型（GMM）不能有效处理重尾噪声下图像拖尾情况，提出了基于拉普拉斯（Laplacian）分布的有限混合模型图像分割方法。与标准拉普拉斯混合模型（LMM）将像素点作为孤立个体不同的是，该方法充分考虑了相邻像素点间的空间关系。相较传统混合模型参数估计采用的EM算法，该方法采用梯度下降法优化参数。实验结果表明在处理重尾噪声时，该方法与标准LMM算法和GMM算法相比，鲁棒性更好，分割更精确有效。

拉普拉斯混合模型（LMM）；图像分割；重尾噪声；空间邻域关系

A

TP391.41

10.3778/j.issn.1002-8331.1301-0256

LUO Lei,WANG Shitong.Laplacian mixture model with neighborhood field for image segmentation.Computer Engineering and Applications,2013,49（13）：133-137.

国家自然科学基金（No.61272210）。

罗雷（1989—），男，硕士，研究领域为人工智能与模式识别；王士同（1964—），男，教授，博士生导师，研究领域为人工智能，模式识别，生物信息学等。E-mail：jnsqyp@126.com

2013-01-23

2013-03-14

1002-8331（2013）13-0133-05