基于流形学习的异常检测算法研究

刘凯伟，张冬梅

中国地质大学 计算机学院，武汉 430074

基于流形学习的异常检测算法研究

刘凯伟，张冬梅

中国地质大学 计算机学院，武汉 430074

1 引言

化探异常识别是成矿预测和资源评价的关键。传统地质统计方法具有无偏、最优等特点，但要求数据呈正态分布，而实际应用往往不符合统计假设；近年来分形理论被大量应用于地球化学异常确定，但基本思路还是采取单元素值来确定背景值，存在需要平滑处理数据以及对样品中特高品位敏感等问题。因此，寻找能体现地球化学数据空间结构和非线形特征的异常识别方法具有重要的研究价值。

针对地质异常现象的不平稳性，即地理空间的有矿样本的数目远远小于无矿样本的数目，化探异常识别从本质上来看是一种不均衡数据的分类问题。传统机器学习分类算法往往基于三点假设[1]：（1）追求最大分类正确率；（2）不同分类错误代价相同；（3）数据集中不同类别包含的样本数目大致相当。在区域化探数据集中有矿、无矿样本数目并不均衡，不符合上述假设，如果采用传统研究方法，处理往往会“偏向”多数类样本即无矿样本而忽略少数类样本即有矿样本，导致将测试样本全部判别为大类，虽然总体分类正确率很高但小类有矿异常样本识别率却非常低。而在成矿识别中，人们更关心的是少数类即有矿样本的分类正确率，因此有效提高少数类的分类性能是成矿异常识别亟待解决的问题。本研究拟将非均衡数据分类问题引入到区域化探异常识别中。

但是随着数据维数的不断增加，面对这些数据集，如何从中发现其中的异常数据仍然是一个难题。为了更好地理解和处理这些高维复杂数据，数据降维技术被广泛应用。数据降维的目的是找出高维数据中隐藏的低维结构，即将原始高维空间映射到低维空间中。目前，在成矿预测中线性数据降维方法仍然是数据分析处理中使用最为广泛的降维方法，如主成分分析（Principal Component Analysis，PCA）[2]等。主成分分析从20世纪90年代至今，在成矿预测中取得了较好的效果。2006年，宋明辉等[3]以东昆仑祁漫塔格研究区为实验区，提出了利用比值分析和主成分分析（PCA）的方法对预测单元进行蚀变遥感异常信息提取，取得了较好的效果。2009年，郭云开[4]等提出一种基于局部能量规则的第二代Curvelet变换和主成分分析（PCA）相结合的影像融合的方法，实验也表明在异常信息的提取上取得了较好的效果。2010年，王瑞国[5]等以内蒙古锡林郭勒盟布鲁特地区为研究区，采用PCA和比值图像处理方法，进行试验区的成矿预测，取得了较好的实际运用效果。但是，地学数据如化探数据，往往是非线性的高维数据，利用线性降维方法很难发掘这类数据的内在结构及非线性分布特征。

为了弥补线性降维方法的不足，针对高维数据的非线性特征，近年来出现了很多非线性降维方法。流形学习是典型的非线性降维方法[6]，通过流形学习方法建立高维-低维映射模型，能更加合理地显示高维数据集的内在结构。因此本文拟将流形学习算法运用在异常检测中，在非线性降维的同时保持原样本空间的分布特性，并在此基础上，将集成学习AdaCost[7]方法嵌入到流形学习算法中，按分类的错误率更新样本的权值，通过关注分类错误的样本，进一步提高少数类样本的分类性能和异常检测的准确率。本文以UCI三组不均衡数据以及另外一组的地学数据为研究对象，进行仿真实验。实验结果表明本文算法预测结果在评价指标上好于传统方法，能更准确地找出异常。

2 流形学习算法理论

2.1 流形学习算法

定义1（流形）流形是微分几何学的一个概念，最早由Riemann在1854年提出，其定义为：设M是一个Hausorff拓扑空间，若M的每一点P都有一个开邻域U⊂M，使得U和n维欧氏空间Rn中的一个开子集同胚，则称M是一个n维拓扑流形，简称为n维流形。

定义2（流形学习）流形学习过程定义为：设Y⊂Rd是一个低维流形，f:Y→RD是一个光滑嵌入，其中D＞d。数据集{yi}是随机生成的，且经过f映射为观察空间的数据{xi=f(yi)}。流形学习就是给定观察样本集的xi条件下重构f和{yi}。

流形学习算法本质是一种非线性的降维方法，即从高维采样数据中恢复低维流形结构，并求出相应的嵌入映射，把高维空间中的数据在低维空间中重新表示，以实现维数约简或者数据简化。常见的流形学习算法有LLE算法[8]、ISOMAP算法[9]、LE算法[10]等。本文主要采取的是LLE算法。

2.2 LLE算法分析

LLE算法的基本步骤如下：

步骤1给的数据集为X，其中Xi∈RD，i=1，2，…，n，n为样本总数，D为原始空间维数，搜索数据集中每个Xi的K个最近邻，{Xi1，Xi2，…，Xik}，Xik∈X，K＜n，对于计算每一个点Xi的近邻点，一般采用K近邻或者ξ邻域。

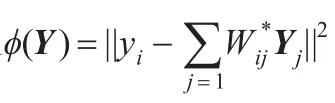
3 异常分类算法理论基础

3.1 代价敏感分类

目前的异常分类算法都强调分类的准确率，并且基于这样一个假设，即所有错误分类的代价都是相等的。但在很多实际应用中，不同类型的错误往往对应不同的分类代价，例如在100个人中，只有1人患有癌症，一个非代价敏感学习算法可能将所有人都分到“健康”这一类，虽然准确率很高，但这个模型是无用的，而且把一个癌症患者诊断为健康的代价也远远高于把一个健康人诊断为绝症的代价。代价敏感分类就是为不同类型的错误分配不同的代价，使得在分类时，高代价错误产生的数量和错误分类的代价总和最小。

3.2 AdaCost算法

AdaCost代价算法是一种高效的误分类代价敏感算法[11]，它是Adaboost算法的一种改进。AdaCost算法保持了Adaboost算法的核心理论，并在权值调整中加入了代价调整函数使其成为了代价敏感算法。其基本思想是利用大量的弱分类器通过一定方法组合起来，这样可以得到一个分类性能很强的强分类器。AdaCost算法的具体描述如下所示。

输入：数据集S={(x1，y1，c1)，…，(xi，yi，ci)，…(xm，ym，cm)}，其中ci∈[0，1]，yi∈{0，1}，迭代次数T，弱分类学习算法WeakLearn；

输出：强分类器H(x)。

Step 2循环迭代；t＜T时循环：

Step 2.1对带有权重的训练样本用WeakLearn算法进行训练学习，得到一个弱分类器ht；

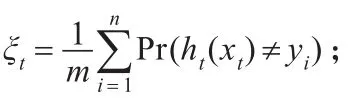
Step 2.3如果ξt≥0.5或者εt=0，则令t=1，返回Step 2；

Step 2.4计算加权参数αi=0.5∗[ln(1-εt)/εt]，选择代价调整函数βi=β(sign(yih(xi))，ci)；

Step 2.5更新样本的权值，Zi为归一化因子：

wt+1(i)=wt(i)exp[-αiyiht(xi)βi]/Zi

Step 2.6t=t+1。

4 基于流形学习的异常检测算法

基于流形学习的异常检测算法首先通过流形学习降维方法生成新的样本数据，新的样本数据集的格式与Ada-Cost算法要求输入的数据集格式完全一致，本文提出的算法具备很好的连贯性。因此可以直接将集成学习AdaCost算法嵌入到新数据集中，按分类的错误率更新样本的权值，进一步提高少数类样本的分类性能，进而提高异常分类的准确率，检测出异常。基于流形学习的AdaCost代价敏感算法基本框架如下所示。

输入：数据集X={x1，x2，…，xn∈RN}，迭代次数T，弱分类学习算法WeakLearn；

输出：强分类器H(x)。

Step 1根据流形学习的降维算法LLE，生成维数较少的数据样本。

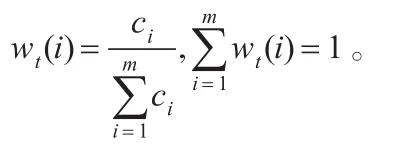
Step 3循环迭代；t＜T时循环：

Step 3.1对将为后的的数据集用WeakLearn算法进行训练学习，得到一个弱分类器ht；

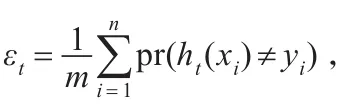
Step 3.3计算加权参数αi=0.5∗[ln(1-εt)/εt]，选择代价调整函数βi=β(sign(yih(xi))，ci)；

Step 3.4更新样本的权值，Zi为归一化因子：

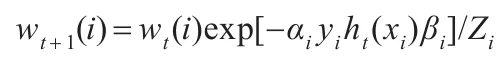
Step 3.5t=t+1；

5 仿真实验

5.1 实验数据

为了验证提出的算法的效果，本文选取UCI数据集中的三组数据以及一组地学化探数据进行仿真实验，从UCI提供的数据集中选择了三组非均衡数据集，这些数据集是国际通用、权威的标准测试数据集。

另外还选取云南个旧锡铜多金属矿床化探数据为研究对象，个旧矿区分布在东北、西北和南北方向多个褶皱断裂带的交汇处[12]，个旧地区是锡铜多金属成矿区。本文选取Sn、Cu、Pb、Zn等39种共计524条1∶20万系沉淀物进行仿真实验，其中已经勘明的有矿点41个，无矿点483个，无矿与有矿的不平衡率为11.78（比例为483∶41），是典型非均衡数据集，符合实验要求。

5.2 仿真实验环境与评价指标

5.2.1 实验仿真环境

本实验使用PC机配置为Pentium®2.92 GHz中央处理器，2 GB内存，操作系统是Windows XP；LLE程序用Matlab语言编制，在Matlab7.0平台上运行，SMO与AdaCost程序在WEKA平台上运行。

5.2.2 实验评价指标

当分类的数据是不均衡数据时，传统的分类方法往往偏向多数类样本，这样会导致少数类的识别率很差，但在实际应用中人们更加关注少数类的分类正确性。因此，单纯将分类精度作为不均衡数据的评价指标并不合理。为了更全面地反映化探异常识别的性能，本文主要引入AUC、G-mean复合指标进行评价。复合指标的定义如下：

定义3（G-mean指标）G-mean也称几何平均准则，由Kubat和Matwin在1997年提出，是一种有效衡量不平衡数据分类效果的准则。

其中，acc+为少数样本的精度，acc-多数样本的精度[1]。如果acc+精度大而acc-精度小，则G-mean值较小；两者精度都很大且保持平衡时，G-mean值较大。G-mean指标综合考虑了两类样本的精度，能更好地衡量不平衡数据分类器的性能。

定义4（AUC指标）ROC曲线能较全面地描述分类器的性能，由于不能定量分析，采用ROCArea值表示[13-14]。ROCArea值表示ROC曲线下的面积（AUC），其计算公式为：

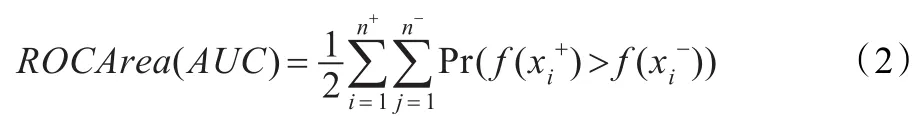
其中，n+为少数类样本的个数，n-为多数类样本的个数。对任一少数类样本，若分类算法f将其分类为少数类的概率大于多数类的概率，则记值越接近1，模型的预测效果越好。

5.3 仿真实验过程描述

首先采用线性降维以及流形学习算法对实验用到的四组数据进行降维处理，将降维后的结果作为新的数据集输入WEKA平台，选择SMO算法作为基分类器，将分类结果同标准SMO算法、基于线性降维的分类算法（PCAAdaCost）、基于流形学习的分类算法（LLE-AdaCost）进行性能对比。

5.4 实验结果与分析

根据上述实验设置，分别对UCI数据以及个旧区域化探数据进行仿真实验。以下是UCI数据与化探数据的实验结果。

5.4.1 UCI数据集

实验结果如表1所示，为方便对比，各算法评测指标表现最好的结果背景用深灰色标出，次好的结果用浅灰色标出。

从表1看出对三组UCI数据的实验，提出的算法在各项评测指标G-mean、AUC的表现均优于采用标准SMO分类器以及基于线性降维的算法，能够有效地检测出异常。

表1 测评指标对比表

5.4.2 化探数据

如表1，如果采用标准SMO分类器，少数类（有矿类）样本的预测效果很差，也就是模型在外推时几乎没有识别出有矿样本，而少数类样本正是要重点关注的，因此标准SMO分类器几乎不能满足实际需求。进一步对比基于线性降维的异常识别算法与本文提出的异常识别算法发现，各项评测指标G-mean、AUC相对基于线性降维的异常识别算法均表现较好，大大提高了少数类样本的分类精度。这是因为集成AdaCost算法更关注少数类样本，通过牺牲多数类的准确率来提高少数类的精度，以达到提高分类器实际性能的目的。

为了进一步说明本文算法的效果，分别采用了柱状图与折线图来显示实验的结果，如图1～图4所示。图1和图2是三种方法在G-mean和AUC上的柱状图对比图。图1和图2中，横坐标代表三组标准UCI数据集以及一组地学数据，从左到右分别为Glass、Hepatitis、Sonar、地学数据；蓝色代表SMO，绿色代表PCA-AdaCost，红色代表LLE-AdaCost。图1和图3中，纵坐标代表G-mean，图2和图4中纵坐标代表AUC。

从图1～图4可以看出，本文提出的异常分类算法（LLE-AdaCost）相比于传统的SOM、PCA-AdaCost，在仿真实验设置的评价指标上表现较好。进一步，在三组标准UCI数据集上以及另外一组地学数据中可以看出，LLE-AdaCost算法在G-mean上优于其他两组的有三个，而另一个不是最优的数据集也优于传统的PCA-AdaCost算法；在AUC上三组标准UCI数据集以及另外一组地学数据中，LLE-AdaCost相对于其他两种传统算法全部是最优的，比PCA-AdaCost算法表现更优。这是由于相对于传统的线性降维方法，通过流形学习建立的高维-低维映射模型，能够更加合理地显示高维数据集的内在结构，在非线性降维的同时保持了原样本空间的分布特性。通过集成的AdaCost算法能够进一步提高少数类样本的分类性能和异常检测的准确率。

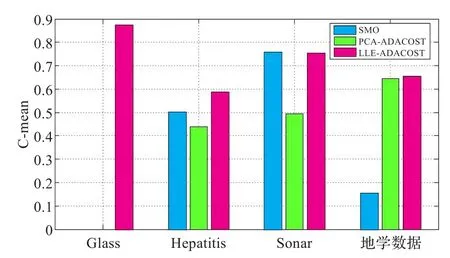
图1 G-mean条形对比图

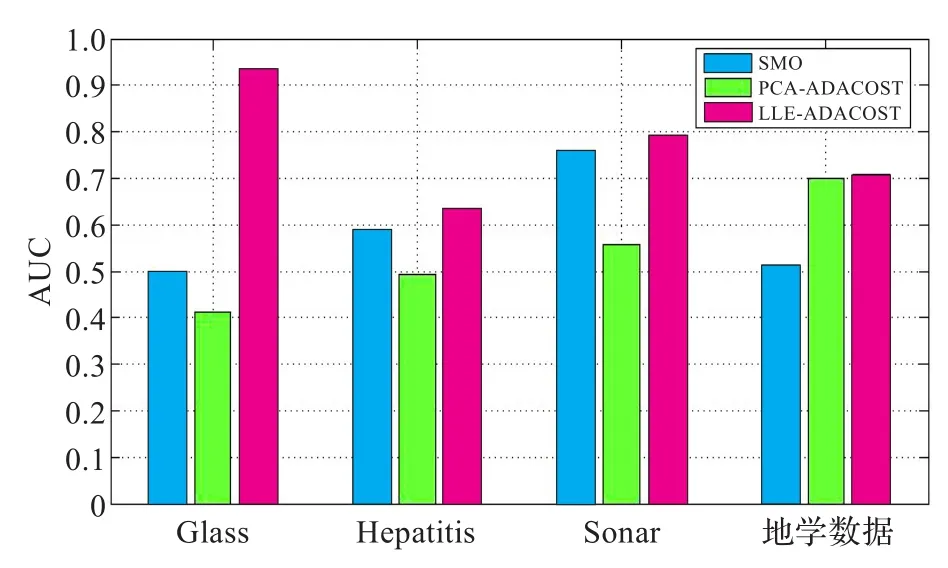
图2 AUC条形对比图

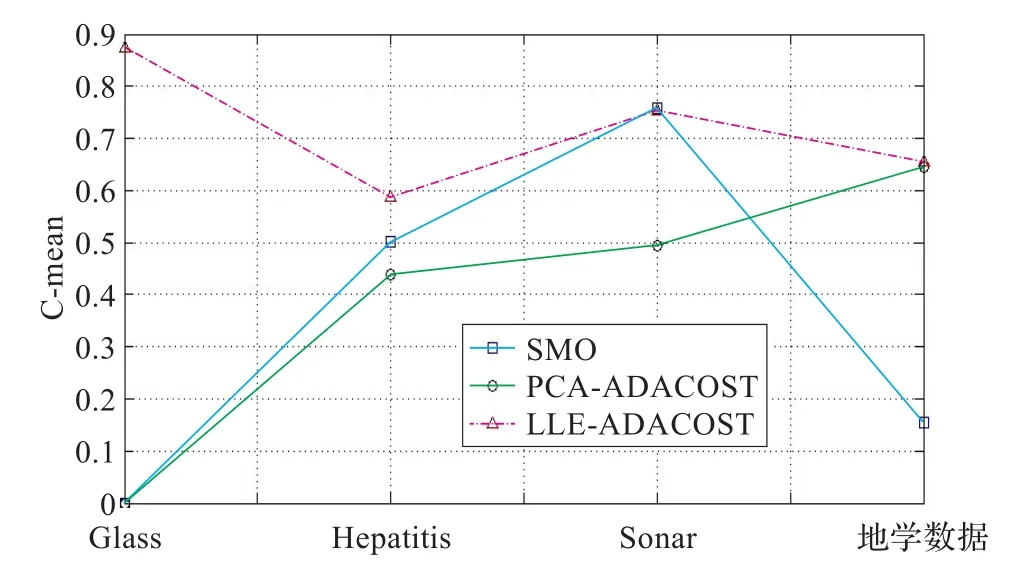
图3 G-mean折线对比图

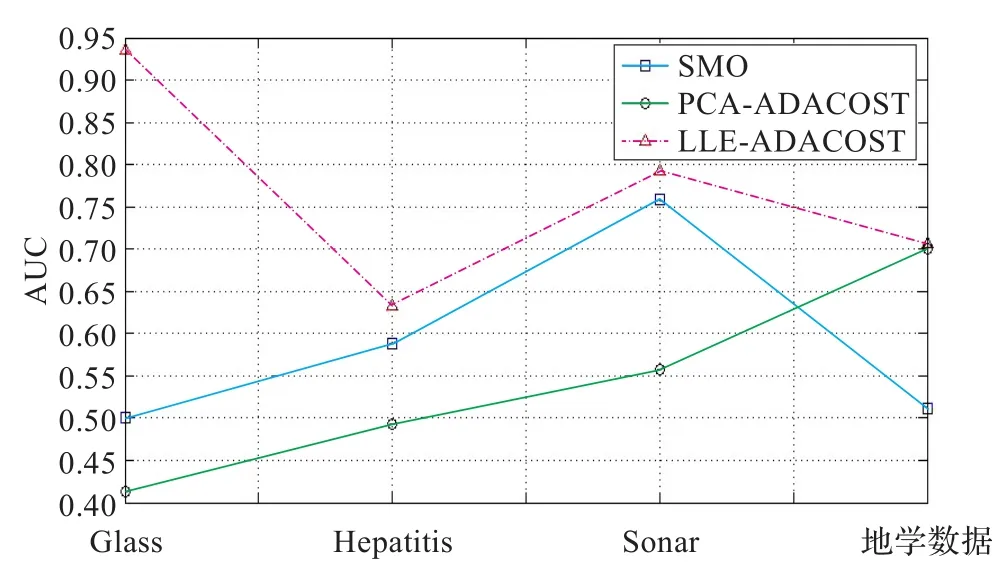
图4 AUC折线对比图

表1显示，以G-mean为评价标准，LLE-AdaCost算法的数据集Sonar不是最优分类方法，这个数据集中多数类与少数类样本数目比例为1.14∶1，维数为60，而这个数据集中最优的方法为传统的SOM。这是由于基于流形学习的代价敏感性学习算法也可能遭遇到Over-Samping的问题，例如过度拟合，这是因为如果给少数类赋以比较大的代价因子等于进一步赋予少数类样本更大的权值，所以产生了过度拟合，致使分类效果有所下降，从而进一步使异常检测效果下降。从表1还可以看出，若以AUC为评价标准则，本文的异常分类算法的关于少数类的分类精度得到了大大提高。基于流形学习的异常检测算法由于流形学习降维算法保证了原始数据结构的完整性，使得降维后的数据符合原始数据的空间分布，分类器的性能得到大大提高。这说明，仅仅以G-measure为评价标准并不能正确地说明分类器的分类效果，以G-mean和AUC为评价标准综合考虑才能正确评价分类器的分类效果，这样才能说明分类的正确性以及少数类分类的正确性，进而才能进一步检测出少数类也就是所说的异常数据。

6 结论

异常数据挖掘在很多领域都具有非常重要的意义，其中少数类的识别即分类性能的提高更令人关注。本文提出了一种新型的基于流形学习的异常检测算法，利用非线性降维方法，通过建立高维-低维映射关系真实地反映出高维数据的数据特征，同时嵌入的集成学习AdaCost代价敏感算法进一步提高了小类异常样本识别率。最后，分别对UCI数据集以及不均衡的地学数据进行仿真实验，实验结果表明，基于流行学习的AdaCost算法预测的结果较传统方法精度更高，为矿产资源定量预测与评价提供了新的解决途径。

[1]Probost F.Machine learning imbalance data sets 101[C]//Proceedings of the AAAI 2000 Workshop on Imbalanced Data Sets，2002.

[2]Jolliffe I T.Principal component analysis[M].New York：Springer， 2002.

[3]宋明辉，潘军，邢立新.东昆仑祁漫塔格地区找矿预测遥感研究[J].吉林大学学报：地球科学版，2006（S1）.

[4]郭云开，董胜光，彭悦.基于Curvelet变换和PCA相结合的方法提取地质构造信息[J].测绘通报，2010（4）.

[5]王瑞国，于涛，李军，等.内蒙古锡林郭勒盟布鲁特地区遥感矿化信息提取及应用[J].测绘与空间地理信息，2010，34（4）.

[6]de Silva V，Tenenbaum J B.Global versus local methods in nonlineardimensionalityreduction[C]//Proceedingsofthe Conference on Neural Information Processing Systems，2003：705-712.

[7]Fan W，Stolfo S J，Zhang J，et al.AdaCost：miss-classification cost-sensitive boosting[C]//Proceedings of the 16th International Conference on Machine Learning，1999：97-105.

[8]Roweis Sam T，Saul Lawrence K.Nonlinear dimensionality reduction by locally linear embedding[J].Science，2000，290（22）：2323-2326.

[9]Tenenbaum J B，Silva V，Langford J C.A global geometirc framework for nonlinear dimensionality reduction[J].Science，2000，290（22）：2319-2323.

[10]Belkin M，Niyogi P.Laplacian eigenmaps for dimensionality reductionanddatarepresentation[J].NeuralComputation，2003，15（6）：1373-1396.

[11]Friedman J H，Olshen R A，Stone C J，et al.Classification and regression trees[M].[S.l.]：American Statistical Association，1986.

[12]刘才泽，胡光道.个旧地区化探数据的各向异性及东西矿区的对比研究[J].地质与勘探，2007，43（6）：81-85.

[13]Fawcet T.ROC graphs；notes and practical considerations for researchers[J].Machine Learning，2004（3）：1-38.

[14]张晓龙，江川.基于AUC的SVM多类分类方法的研究[J].计算机工程与应用，2007，43（14）：166-169.

LIU Kaiwei,ZHANG Dongmei

School of Computer Science,China University of Geosciences,Wuhan 430074,China

Anomaly detection has important significance in many fields.Essentially speaking,the recognition of geochemical anomalies is the problem of imbalanced data classification.The main problems faced by anomaly identification is the processing problems of high-dimensional data,manifold learning is a nonlinear dimensionality reduction method that can reasonably reduce the data dimension.Therefore this paper proposes an anomaly detection algorithm based on the manifold learning,through manifold learning to achieve the dimension reduction,the new algorithm combines AdaCost technology of integrated learning,to improve classification performance.The new algorithm is based on the simulation experiment on the research objection of polymetallic deposits such as tin and copper from Gejiu,Yunnan province.The experimental results show that predicted results for the new algorithm delineating regional geochemical anomalies are better than traditional methods,which can more accurately identify the forming-ore abnormality.

anomaly detection;unbalanced data;manifold learning;cost-sensitive learning

化探异常识别是成矿预测的重要依据。化探异常识别本质上是一不均衡数据的分类问题。异常识别过程中面临的主要问题是高维数据的处理问题，流形学习通过非线性降维方法实现维数约简。提出了一种基于流形学习的异常识别算法，通过流形学习进行维数约简，结合AdaCost技术，以改善不平衡数据的分类性能。以某锡铜多金属矿床的数据为研究对象进行仿真实验，实验结果表明该算法能够更准确地圈定区域化探异常，为成矿预测与评价提供了新的解决途径。

异常检测分类；不均衡数据；流形学习；代价敏感学习

A

TP181

10.3778/j.issn.1002-8331.1111-0210

LIU Kaiwei,ZHANG Dongmei.Manifold learning-based anomaly detection algorithm.Computer Engineering and Applications,2013,49（13）：105-109.

国家自然科学基金（No.40972206）；中央高校基本科研业务费专项资金资助项目（No.1323520909）。

刘凯伟（1987—），男，硕士研究生，主要研究领域为数据挖掘与智能计算；张冬梅（1972—），女，博士，教授，主要研究领域为科学计算可视化，智能计算，智能信息处理等。E-mail：373907551@qq.com

2011-11-16

2012-02-17

1002-8331（2013）13-0105-05

CNKI出版日期：2012-04-25http://www.cnki.net/kcms/detail/11.2127.TP.20120425.1721.064.html