一种通信网络抗毁性评价的改进模型

蔡瑾曜，吴玲达

1.装备学院 研究生管理大队，北京 101416 2.装备学院 重点实验室，北京 101416

一种通信网络抗毁性评价的改进模型

蔡瑾曜1，吴玲达2

1.装备学院 研究生管理大队，北京 101416 2.装备学院 重点实验室，北京 101416

1 引言

现代信息化条件下的高技术战争已经从平台中心站转向网络中心站，未来战争中网络化作战模式越来越受到重视。然而随着信息网络技术的发展，针对通信网络的攻击也急剧上升，使得网络可靠性和安全度[1]大大下降，网络战争已经成为影响战争胜负的关键[2-3]。通信网络是网络化战争中最基本、最基础的研究内容之一，同时，通信网络往往是敌方打击的首选目标。因此通信网络如何在复杂的战场环境中满足战场通信要求，将在现代化战争中起到关键作用。

网络的抗毁性是从图论的概念中提出并发展而来的，在通信网的抗毁性分析中得到广泛应用，尤其在军事通信网中更是一个非常重要的概念。对于一个网络而言，网络抗毁性是指：当网络中出现确定性或随机性故障时，网络维持或恢复性能达到可接受程度的能力。确定一种定量有效的评价方法，是实现上述分析通信网的抗毁性能的基础。

针对现有的一些通信网抗毁性分析成果存在无法正确评价节点重要度，以及不能满足不同节点数的网络间的抗毁性分析与比较等不足，本文在已有的分析方法基础上，给出了一种基于节点的网络抗毁性评价改进方法，并验证了该方法的有效性。

2 现有通信网抗毁性评价方法概述

网络抗毁性能[4-6]和节点重要性[7-9]在通信网的分析和设计中具有重要意义。国内外有不少文献就网络拓扑结构的抗毁测度进行了论述，主要有基于割集信息、最小割集或最弱割集的全局性网络拓扑结构抗毁性度量[4]，基于熵的网络拓扑结构抗毁性度量[5]，基于节点的抗毁性度量值均方差的评估模型[6]和跳面节点法[7]等。节点重要性的评价方法主要有生成数目法[8]、网络凝聚度[9]、最短路径法等。研究发现，上述模型和方法各有其评估侧重点，也各有其局限所在，不具有普遍适用性。

通过深入研究文献[10]中抗毁性评价模型，发现利用跳面节点法来计算节点重要度不具有普遍适用性。跳面节点法只能体现跳面数、跳面节点数以及跳面间链路数，当这三者都相同时即认为两个节点具有相同的重要性，但并不能完完全全反映出各节点之间连接的细节。以图1所示的网络为例，跳面节点法的评价结果为节点2和节点5的相对重要性相同，显然不正确。因为节点5为网络割点，一旦失效则导致网络变得不连通，而节点2为非割点，即使失效全网仍保持连通，因此，节点5比节点2重要。

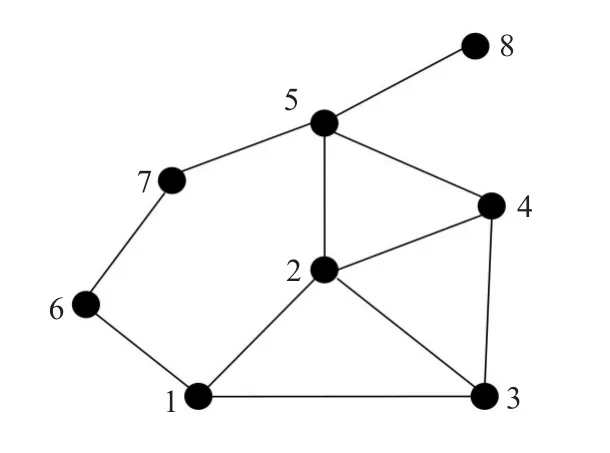
图1 通信网络拓扑结构图

另外，该抗毁性评价模型只能对某一个网络进行抗毁性评价或者是对节点数相同的不同网络之间进行评价，而无法对节点数不同的通信网络之间进行抗毁性能比较。针对上述两方面的不足，本文首先给出了基于最短路径数和跳面节点法节点重要性多指标评价方法，同时提出了一种基于节点的全网平均等效抗毁性测度的网络抗毁性评价模型，对不同节点数的网络进行抗毁性评价，全网平均等效抗毁性测度值越大，网络的抗毁能力越强。

3 基于节点的通信网抗毁性改进模型

3.1 全网平均等效抗毁性测度

经过实验分析，发现文献[11]中模型对不同节点数的网络进行抗毁性评价时不具有可操作性。因为节点数大的网络必然比节点数小的网络要多出它们节点数之差的CM(k)值，这样就无法评价它们之间抗毁性的强弱。我们发现全连通网络是结构最优的网络，也是抗毁性最强的网络，只是基于建设成本和运行效率等因素的考虑，现实中的网络很少采用全连通网络结构。本文研究发现，可以将网络抗毁性评价的着眼点放在实际网络与全连通网络的结构差异上，由此，在上述模型的基础上提出了一种基于节点的全网平均等效抗毁性测度的网络抗毁性评价模型。

假定给定网络节点的数量是N，那么网络抗毁性的测度指标[11]定义式为：

CM(0)为网络G的连通度；CM(k)为从网络中删除一个重要节点后所得到的网络的连通度；n是使网络完全失去连接（所有的节点都是孤立的，彼此没有连接）之前必须删除的节点的数量。CM(k)由下式给出：

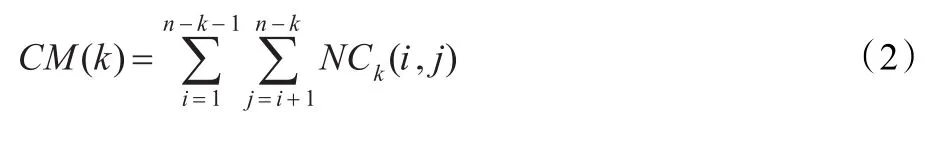
其中，NCk(i，j)是网络Gk中节点i与节点j的连通度；n-k是Gk的节点数；x是节点i与节点j之间独立路径的数目；JN(t)是这些路径的跳数。将式（2）和（3）带入式（1）计算出SM(G)的值，对网络的抗毁性进行评价。

在此基础上，给出网络抗毁性测度的新指标即抗毁性测度均值和全网平均等效抗毁性测度。

定义1

P定义为网络抗毁性测度均值，N为该网络的结点个数，i是总共删除节点的个数。对于一个节点数为N的全连通网络，按照上面抗毁性测度的算法易知：

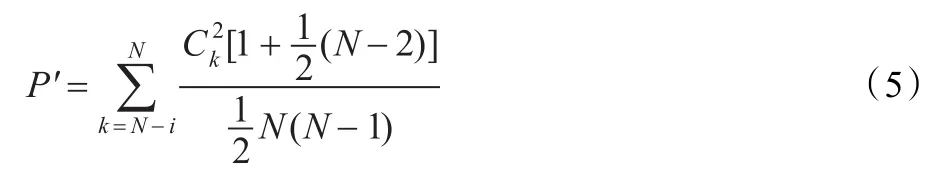
定义2全网平均等效抗毁性测度指标定义为：

由于全连通网络的特性，所以对于确定节点数的任意结构的网络，全连通网络的网络抗毁性测度是最大的，式（8）的分子就是全连通网络的网络抗毁性测度。因而任意非连通网络的等效抗毁性测度0≤D＜1，D的值越大，网络抗毁性越强。这样任意的网络的抗毁性都可归结为全网平均等效抗毁性测度这一指标，就解决了节点数不同网络之间抗毁性比较的问题。

3.2 节点重要性评价改进方法

在进行网络抗毁性分析时，对节点重要度的评价是十分重要的一环。如果不能正确评价节点重要度，将导致上述方法计算的抗毁性值比实际偏大，影响分析结果。通常情况下把节点的度数作为衡量重要性的指标，认为与该节点直接连接的边越多该点重要度就越大。但是这种思想往往忽略了节点和节点之间的连接情况，是不完备的。假设一个节点的度数不是所有节点中最高的，但它到其他各节点之间的路径数都非常短，这表明该节点与其他节点联系都很紧密，处于核心的位置，则该节点一旦被攻击整个通信网络就会瘫痪，此节点的重要性不言而喻。

前文已经阐述了利用跳面节点法来评价节点重要性的缺陷，这里将基于最短路径数的方法[12]与跳面节点法结合起来，进行多指标评价。深入研究发现，最短路径数方法虽然能解决跳面节点法对于节点之间连接细节的缺陷，但是它只考虑了最短路径数目，舍弃了其他更长的迂回路径，对节点数相对较多的网络结构的判断会失去精度；而跳面节点法则能体现跳面数、跳面节点数以及跳面间链路数，对节点数较大，结构较复杂的网络分析更具有层次感，能弥补最短路径法的不足。

下面给出了节点重要度地加权指标值的定义为：

Inv是最短路径数的节点重要性指标；Si是跳面节点法的节点重要性指标；α和β分别是它们的权值。则节点重要度就可以用指标Mv来确定。

基于最短路径数方法的节点重要度定义为：

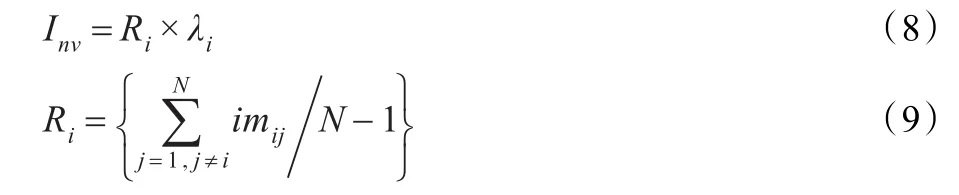
其中，Ri为基于最短路径数的节点重要度；λi为节点i的权重值。这里给出等效最短路径数的定义：

对于一个N节点的网络，如果节点i与节点j之间有mij条长度为kmin的最短路径，则节点i与节点j之间的等效最短路径数为：

其中，μ(kmin)是相应N节点全连通网络中节点间不大于kmin步的路径数。显然，0＜imij≤1，当且仅当两节点之间有直连边时，imij=1。对于任意的i与j，若imij=1，则为全连通网络。

跳面节点法的节点重要度定义为：

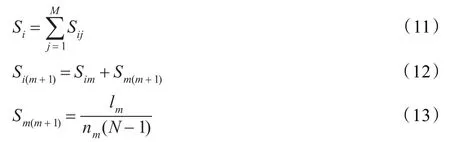
式中，n为第m跳面上的节点数目；第(m+1)跳面上的节点数目为n(m+1)，2跳面的连接链路数为lm。

对于α和β值的确定，给出如下处理方法：

网络节点数N＜10，α=0.7；相反α=0.3。

3.3 基于节点的通信网改进模型标准和流程

本文将通信网的攻击看成是通信网络节点和链路逐步失效的过程。对通信网抗毁性能的分析除了考虑网络节点完整时的抗毁性能，还包括了节点逐个失效时它们的抗毁性能，并将节点完整和节点逐步失效时的连通性能之和作为整个网络抗毁性的度量值，从而得出全网平均等效抗毁性测度D，D越大则认为抗毁性越强。

为了便于计算仿真，假设通信网络中的节点只有两种工作状态，即工作和失效。网络中节点工作状态也是相互独立的，彼此不受影响。通信网抗毁性分析程序步骤如下：

（1）根据网络拓扑图，输入当时拓扑结构中N个节点的网络邻接矩阵R。

（2）计算任意节点对之间的最短路长k和等效最短路径数。

（3）计算此时通信网络的连通性能（连通度）。

（4）计算通信网络各节点的重要度，并删除最重要的一个节点。

（5）判断是否所有节点都孤立，若不是，转到步骤1；若是，转到步骤（6）。

（6）计算所有连通度之和。

（7）得出全网平均等效抗毁性测度D。

图2给出了基于节点的通信网改进模型的流程图。

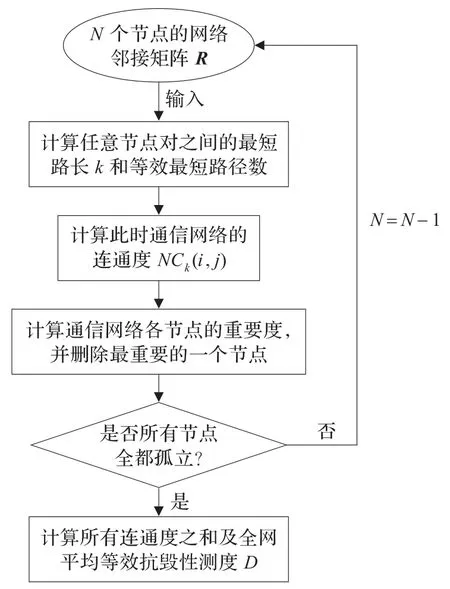
图2 改进模型流程图

4 实验分析

现有两个实际电力通信网络G1和G2，拓扑结构如图3、4所示，分别对它们进行网络的抗毁性计算。为了便于仿真实现，限定本文所有节点和链路的权重λi为1，同时在节点删除过程中，与之相连的链路也随之失效。

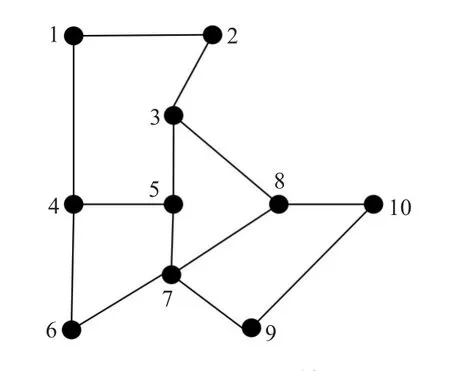
图3 G1网络拓扑结构图

图4 G2网络拓扑结构图

利用3.3节中的计算流程对G1、G2的分析结果，分别如表1和表2所示。

从实验分析结果中可以看出网络G1抗毁性比G2强，这是由于G2中节点4、5是处于上下层中间的两个关键节点，一旦被攻击，整个拓扑结构就会上下不能兼顾，网络就会陷入瘫痪，G2的抗毁性很差。显然G1抗毁性比G2强，符合实际情况。

在这里对图1所示通信网络进行节点重要度评价，利用本文描述的方法得出节点5的重要度比节点2高，这显然是与实际相符的。如果利用跳面节点法来评价节点重要度，则会认为节点2和5重要度一样，再对其抗毁性测度计算时，会出现很大偏差，因为如果第一次删除的节点不是最重要的节点，那么最终计算得到的抗毁性测度会偏大与实际不符。如图1网络所示，因节点重要度评价不准而先删除了节点2最终得到网络抗毁测度SM=55.716 7；而利用改进的节点重要度评价算法最终计算得到的抗毁性测度SM*=51.933 3。显然，原方法夸大了通信网路的抗毁性，给实验分析带来了误差。

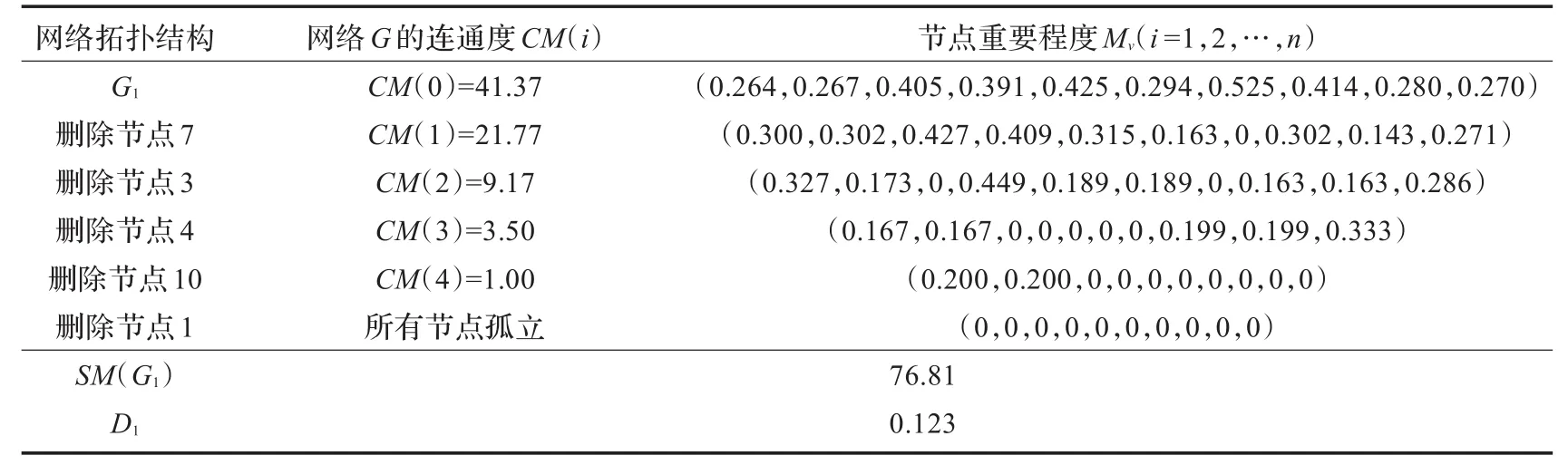
表1 G1网络抗毁性测度计算

表2 G2网络抗毁性测度计算

5 结束语

本文在以网络抗毁性测度分析模型的基础上，指出了现在此模型中利用跳面节点法评价节点重要度的缺陷和不足，结合基于最短路径数的方法对该模型进行完善；同时提出了一种基于节点的全网平均等效抗毁性测度的网络抗毁性评价模型，可以较有效地对不同节点数目的网络进行抗毁性分析和相互比较，为评价通信网络的抗毁性提供了一个可靠的定量标准和简单有效的计算方法。本文提出的方法全都是基于无权网络，而实际的网络往往涉及很多其他因素，下一步可以结合节点本身重要度和抗毁性以及链路传输宽带和速度等因素，综合评价网络抗毁性。

[1]谭小彬.基于多层次多角度分析的网络安全态势分析[J].信息网络安，2008（11）：56-63.

[2]叶征.浅析网络战争[J].国际电子战，2009（6）：12-13.

[3]陶陶.未来战争网络决定胜负[J].科学之友，2009（3）：90-91.

[4]Lin W，Varshney P K.On survivability measures for military networks[C]//Proceedings of the IEEE Communications Conference.[S.l.]：IEEE Press，1990：1120-1124.

[5]Schroeder M A，Newport K T.Tactical network survivability through connectivity optimization[C]//Proceedings of the IEEE Military Communications Conference.[S.l.]：IEEE Press，1987：590-597.

[6]陈建国，张永静.通信网络拓扑抗毁性评估算法研究[J].通信系统与网络技术，2006，32（1）：6-7.

[7]郭伟.野战地域通信网可靠性的评价方法[J].电子学报，2000，28（1）：3-6.

[8]陈勇，胡爱群，胡啸.通信网络中节点重要性的评价方法[J].通信学报，2004，25（8）：129-134.

[9]谭跃进，吴俊，邓宏钟.复杂网络中节点重要度评估的收缩方法[J].系统工程理论与实践，2006（11）：79-83.

[10]唐新强.基于节点的地域通信网抗毁性评价及应用[J].通信系统与网络技术，2008，34（2）：11-15.

[11]Kang H，Butler C，Yang Q.A new survivability measure for military communication networks[C]//Proceedings of IEEE MILCOM’98，Boston，MA，USA，1998：71-75.

[12]绕育萍，林竞羽，侯德亭.基于最短路径数的网络抗毁性评价方法[J].通信学报，2009，30（4）：113-118.

[13]张琨，谈革新，庄克琛.复杂网络抗毁性测度研究综述[J].计算机时代，2010（5）：5-7.

CAI Jinyao1,WU Lingda2

1.Graduate Management Team,Academy of Equipment,Beijing 101416,China
2.The Key Laboratory,Academy of Equipment,Beijing 101416,China

Deeply analyzing the requirements of invulnerability evaluation on communication network,and according to the problem that the existing invulnerability evaluation model is unable to evaluate invulnerability measure node importance and the invulnerability on networks of different numbers of nodes,an improvement is made combined with the evaluation method of node importance with respect to multiple performance measures based on the shortest route number.In addition,an invulnerability measure evaluation model of whole network average equivalent based on nodes is proposed with it,which is validated to be effective.

network topology;node importance;shortest route;invulnerability measure

分析了现代战场通信网抗毁性评价的需求，针对现有通信网抗毁性测度评价模型无法准确评价网络抗毁性测度和节点重要性，以及不同节点数的网络间抗毁性的问题，利用基于最短路径数和跳面节点法节点重要性多指标评价方法对该模型进行改进。在此基础上，提出一种基于节点的全网平均等效抗毁性测度的网络抗毁性评价模型，并验证了模型的有效性。

网络拓扑；节点重要性；最短路径；抗毁性测度

A

TN915.02

10.3778/j.issn.1002-8331.1112-0611

CAI Jinyao,WU Lingda.Improved invulnerability evaluation model on communication network.Computer Engineering and Applications,2013,49（13）：85-88.

蔡瑾曜（1988—），男，硕士研究生，主要研究领域为：天基通信网抗毁性。E-mail：caijinyao_52@163.com

2012-01-09

2012-04-09

1002-8331（2013）13-0085-04

CNKI出版日期：2012-05-21http://www.cnki.net/kcms/detail/11.2127.TP.20120521.1137.008.html