非强占有限优先权M/M/1排队系统

黄业文，吴红，王远世

1.华南理工大学 广州学院，广州 510800

2.中山大学 数学与计算科学学院，广州 510275

非强占有限优先权M/M/1排队系统

黄业文1，吴红2，王远世2

1.华南理工大学 广州学院，广州 510800

2.中山大学 数学与计算科学学院，广州 510275

1 引言

如今人们的日常工作、生活与互联网络的关系越来越密切，常常要求在网络通讯中既要保持某类服务的优先性又要保证整体网络的稳定性。例如一个节点上有一台服务器，服务器的多台终端进行不同课程的远程实时教学，同时少部分终端在进行教学研讨以及教学反馈等，此时既要优先保证实时教学视频流传输，同时也要保证少数终端的教学讨论等正常网络活动。如何同时满足这两方面的要求，是一个十分有意义的研究课题，涉及到了优先权排队系统的讨论。文献[1]对强占及非强占优先权系统进行基本研究；文献[2-5]讨论分析了几种优先级系统的性能；文献[6-11]更为深入地研究了非强占优先权的排队系统。从非强占优先权排队系统的研究[1]知道，在有优先权的排队系统中如果所有数据帧大部分有优先权时，则有优先权的数据帧的平均等待时间并不会缩短多少，此时，无优先权的数据帧的平均等待时间却会大大延长，甚至有时候会产生严重的队列拥塞，导致排队系统崩溃的结果。如果直接将优先权排队系统在实时视频流传输中进行应用，可能会产生服务器被实时视频流报文长时期霸占的无解状态。因此需要对优先权进行限制，目的为了解除优先权队列源比较大的报文长期霸占服务器的状态，使得在有限优先权下，系统能够很好地继续进行服务，稳定性较好，不至于产生系统崩溃。本文以有限优先权的报文在Internet中的传输为模型，对非强占有限优先权M/M/1排队系统进行研究。

2 系统假设

非强占有限优先权M/M/1排队系统假设如下：

（1）顾客分为两个等级，第1级享有最高优先权，第2级享有次优先权。

（2）顾客到达系统服从参数为λi的Poisson分布，λi为第i级顾客的平均到达率，i=1，2。

（3）服务员为每一级别的顾客服务的时间均服从参数为μ的负指数分布，平均服务时间为，μ为第i级顾客的平均服务率，i=1，2。

3 系统理论分析

3.1 系统队长与等待队长

对于整个排队系统，不区分第1级还是第2级顾客，那么该系统是一个顾客按参数λ的Poisson分布到达，到达的时间间隔和服务员为每个顾客服务的时间均服从负指数分布，平均服务率为μ的M/M/1排队系统，得系统平均队长[1]：

系统平均等待队长[1]：

3.2 顾客在系统中的等待时间

在系统平稳之后，当第1级顾客A到达系统时，若系统空闲，则可直接接受服务员服务；若服务员正忙着，他不能强占服务员进行服务，而只能在部分第2级顾客前排队等待服务。当第2级顾客B到达系统时，若系统空闲，则可直接接受服务员服务；若服务员正忙着，他或者由于系统之前服务了α个第1级顾客而插队排在队伍前面的位置，或者只能排在队末等待服务。记排队等待服务的第i级顾客平均人数为Lqi，第i级顾客的平均排队等待时间是Wqi，其中i=1，2。分两种情况讨论：

（a）到达系统的顾客为第1级顾客A。

（b）到达系统的顾客为第2级顾客B。

先讨论第1种情况（a），到达系统的顾客为第1级顾客A，把两队列合并排队，这时顾客A在系统中所用的平均等待排队时间分为3种情形（aj），记第i级顾客排队等待服务的平均人数为Lqiaj，平均等待时间为Wqiaj，i=1，2，j=1，2，3。对这3种情形的讨论如下。

（a1）第2级顾客足够按间隔α插位排队。此时，第1级顾客A在系统中所用的平均等待排队时间Wq1a1由两部分组成：

（1）顾客A排在队末等待在其之前排队的顾客平均服务时间之和T1：

（2）等待正在服务的服务员空闲出来的平均时间T2。剩余服务时间记作Se，其均值为：

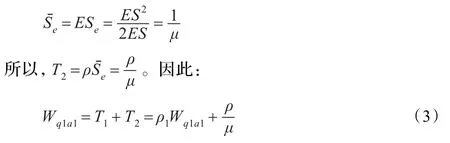
（a2）第2级顾客不足够按间隔α插位排队，在A排队等待期间，陆续到达的第2级顾客仍不足够按间隔α插位排队。第1级顾客A到来的时候，他就排在队末等待服务，在A等待服务期间到来的第2级顾客会排在A之前进行服务，因此A在系统中所用的平均等待排队时间Wq1a2由3部分组成：

（1）顾客A排在队末等待在其之前排队的顾客平均服务时间之和T1=ρ1Wq1a2。

（3）在顾客A排队等待期间，陆续到达的第2级顾客优先插队造成的平均耽误时间之和T3。由于顾客A所需排队等待时间为Wq1a2，在此期间内，第2级顾客到达的平均人数为Wq1a2λ2，其需要的平均服务时间T3=Wq1a2λ2ES2=ρ2Wq1a2，因此可得：

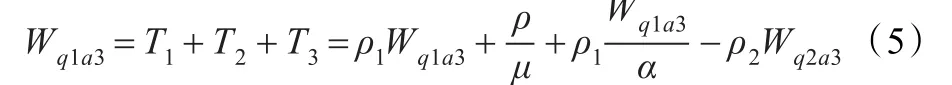
其中，T1、T2类似（a2）情形所求。

再接着讨论第2种情况（b）。到达系统的顾客为第2级顾客B，将两队队列分开排队进行讨论，这时，该顾客B在系统中所用的平均等待排队时间亦分为3种情形（bj），记第i级顾客排队等待服务的平均人数为Lqibj，平均等待时间为Wqibj，i=1，2，j=1，2，3。对这3种情形的讨论如下。

（b1）第2级顾客不足够按间隔α插位排队。Wq2b1由两部分组成：

（1）正在排队等待服务的排在顾客B之前的第1级顾客和全部第2级顾客平均服务时间之和T1。此时，第2级顾客平均排队等待时间为ρ2Wq2b1，则相应的第1级顾客排队等待时间为αρ2Wq2b1。

插队排进顾客B的时候，系统正在服务的顾客是随机的，因此一般情况下在B之前的第1级顾客不会刚好是第2级顾客的α倍，若系统当时排队队列的第1位顾客不是第2级顾客，这时第1级顾客数会比第2级顾客数的α倍要多。总之，在B之前会插队排进比第2级顾客的α倍更多的第1级顾客，多出的第1级顾客数在0到α之间，记多出的平均插队人数为b，则b个顾客接受服务的时间为，

下面计算b的值，有3种计算方法：

②Poisson概率法。当B到达系统时，若正在接受服务的顾客为第2级顾客，其后应该接着排的是α个第1级顾客，然后又是1个第2级顾客……则B之前会多出α个第1级顾客插队排队。这个事件出现的概率可以归结为出现1个第2级顾客的概率p(1，λ2)；若当B到达系统时，发现正在接受服务的顾客为第1级顾客，之后是第2级顾客，则B之前会多出0个第1级顾客插队排队。这个事件的概率等于出现1个第1级顾客的概率p(1，λ1)；若B到达系统排队时，发现正在接受服务的顾客为第1级顾客，之后是1个第1级顾客，接着是1个第2级顾客，此时B之前会多出1个第1级顾客插队排队。该事件的概率为p(2，λ2)……。由此可得：

③系统概率法。类似于Poisson概率法的讨论，只是计算概率时以第1级顾客出现1个的概率为ρ1，第2级顾客出现1个的概率为ρ2来进行计算，因此

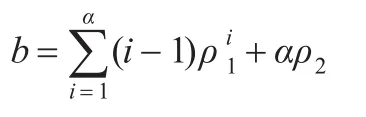
以上就是计算b值的3种方法，在用Matlab模拟实验得出最优方法为系统概率法。

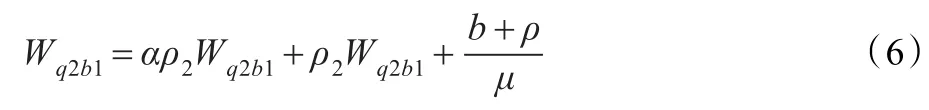
（b2）第2级顾客足够按间隔α插位排队，在顾客B排队等待期间，陆续到达第1级顾客后，第2级顾客仍足够按间隔插插位排队。第2级顾客B在系统中所用的平均等待排队时间由3部分组成。

（1）正在排队等待服务的所有第1级顾客和第2级顾客平均服务时间之和：

（2）等待正在服务的服务员空闲出来的平均时间：

（3）在顾客B排队等待期间，陆续到达的第1级顾客优先插队造成的平均耽误时间之和T3。第1级顾客到达的平均人数为Wq2b2λ1，其需要的平均服务时间为T3=Wq2b2λ1ES1= ρ1Wq2b2，因此可得：

（b3）第2级顾客足够按间隔α插位排队，在顾客B排队等待期间，陆续到达第1级顾客后，第2级顾客不足够按间隔α插位排队。在顾客B排队等待期间，陆续到达的第1级顾客优先插队在顾客B之前的m个顾客造成的平均耽误时间之和T3。这里顾客数m由两部分构成，第一部分是插队排在顾客B之前的陆续到达的αWq2b3λ2-Wq1b3λ1个第1级顾客，第二部分是由于随机情况产生的b个插队排队人数，b的确定参照（b1），所以

因此，可得：

其中，T1、T2类似（b2）情形所求。

这时发现：

因为对于顾客B，（b1）和（b3）情形都是属于第2级顾客不足够按间隔α插位排队的情形。

相等的还有：

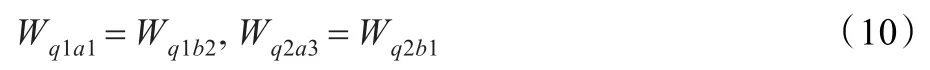
由式（3）～（10），解得：

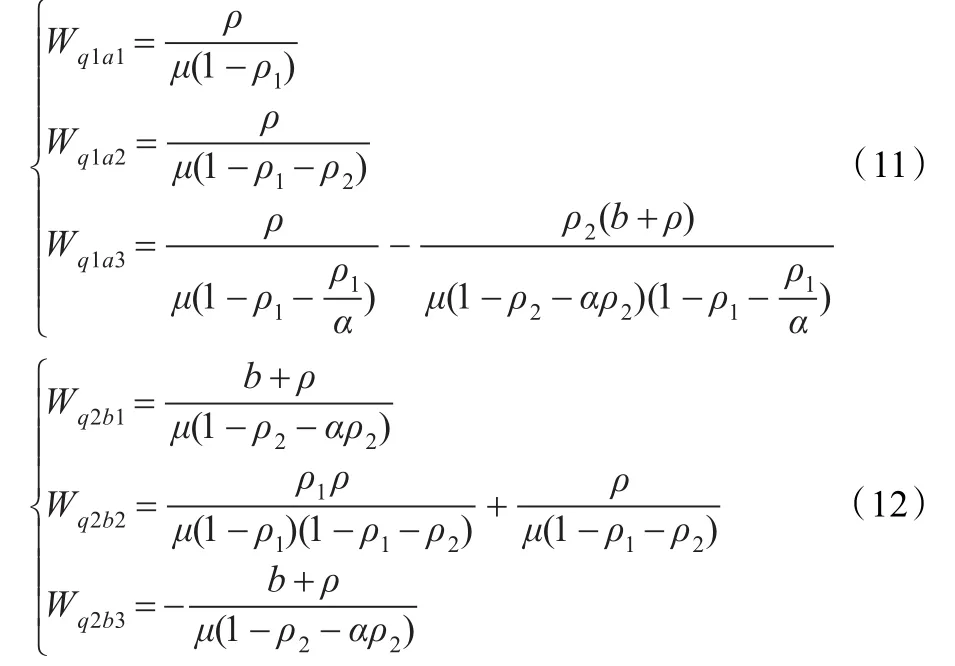
下面计算各种情形出现的概率，记lsi为系统内第i级排队等待的顾客数，i=1，2，包括正被服务和排队等候的顾客，

先计算（b1）情形的概率pb1，此时ls1≥αls2，所以

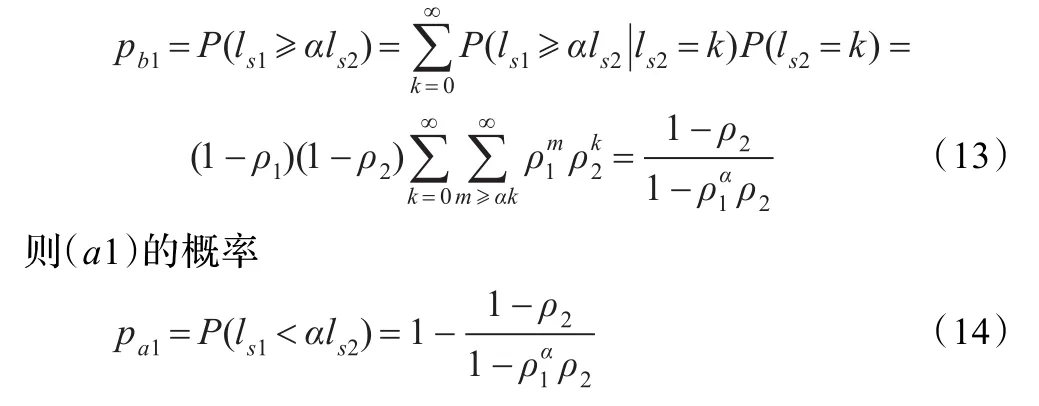
3.3 顾客在系统中的逗留时间

顾客在系统中的平均逗留时间等于顾客在系统中的平均排队时间加上平均服务时间。记Wsi为第i级顾客在系统中的平均逗留时间，则

3.4 不同优先级的队长

第1、2级顾客在系统内等待的平均等待队长：

4 模拟实验结果

为验证理论的正确性，用Matlab进行模拟实验。表1给出了λ1=2.85，λ2=0.15，α=3，μ取不同值的几种结果，其中λ1、λ2单位τ为512 bit时间。

表1 λ1=2.85，λ2=0.15，α=3，μ取不同值的结果

下面比较非强占有限优先权排队系统和一般的非强占优先权排队系统在不同情况下的运行结果，取λ1=3.85，λ2=0.15，μ=5，α=10作为有限优先权模型进行模拟。同时，由于当参数α=∞时，模型就变成第1组有完全优先权的非强占优先权排队系统模型，可以取α=100和α=10 000进行模拟。当第1级顾客被服务1 000次时，统计1次各项平均数据，一共统计100次，其第2级顾客平均排队等待时间结果对比，如图1所示。

图1 λ1=3.85，λ2=0.15，μ=5的第2级顾客平均排队等待时间图

5 结论

由模拟实验知，本文讨论非强占有限优先权M/M/1排队系统时，提出的系统概率法得出的理论结果是恰当的，并且本文模型相对一般非强占优先权排队模型，其系统顾客等待时间更加趋于稳定，更好地规避了系统崩溃风险。本文模型是为了解决计算机网络应用中碰到的远程教育视频流传输问题提出的，至此本文给出了诸如顾客在系统中的等待时间等一些较好的结果，对问题的解决起到了一定的作用。但本文的研究工作只是初步的，例如实际中服务器可能不止一台，而且本文对顾客到来假设服从Poisson分布也可以进行改进。下一步将对模型进行完善，使模型有更好的实际应用价值。

[1]陆传赉.排队论[M].北京：北京邮电大学出版社，1993.

[2]Eng K Y.A photogenic knockout switch for high-speed packet networks[J].IEEE J Select Areas Commun，1988，6（7）：1107-1115.

[3]Hluchyi M G，Karol M J.Queuing in high-performance packet switching[J].IEEE J Select Areas Commun，1988，6（9）：1587-1597.

[4]Iliadis I，Denzel W E.Analysis of packet switches with input andoutputqueuing[J].IEEETransonCommun，1993，41（5）：731-740.

[5]Delre E，Fantacci R.Performance evaluation of input and output queuing techniques in ATM switching systems[J].IEEE Trans on Commun，1993，41（10）：1565-1575.

[6]Krishna Reedy G V，Nadarajan R.A nonpreemptive priority multiserver queueing system with general bulk service and hetergeneous arrivals[J].Computers and Operations Research，1993，20（4）：447-453.

[7]Kapadia A S.Analysis of a finite capacity nonpreemptive priority queue[J].Computers and Operations Research，1984，11（3）：337-343.

[8]宁玉新.一种处理多优先级业务的新模型[J].青岛大学学报，2002，17（3）：1-6.

[9]王科，舒勤，李成.信元调度中的优先级排队研究[J].通信技术，2009，42（11）：133-137.

[10]侯冬倩.反馈后优先非抢占的M/M/1排队系统的等待队长分析[J].山东理工大学学报：自然科学版，2009，23（3）：4-7.

[11]边军辉，尹文运，庞秀梅，等.M/G/1的反馈后优先排队但非抢占的排队系统的初步分析[J].江汉大学学报：自然科学版，2010，38（1）：8-9.

HUANG Yewen1,WU Hong2,WANG Yuanshi2

1.Guangzhou College,South China University of Technology,Guangzhou 510800,China
2.School of Mathematics and Computational Science,Sun Yat-Sen University,Guangzhou 510275,China

The limited-priority concept is raised based on the practical application on the transmission of a real-time video stream of computer network packet（cell）and a non-preemptive limited-priority M/M/1 queuing system is founded.To analyze and study the system,it deduces the average waiting time,the average dwell time and average queue length while customers stay in the queuing system.

queuing theory;non-preemptive;limited-priority;M/M/1 queuing system

以计算机网络中实时视频流传输的实际应用为基础，建立非强占有限优先权M/M/1排队系统模型；对该系统模型进行分析研究，推导出顾客在系统内的的平均等待时间、平均逗留时间和平均队长。

排队论；非强占；有限优先权；M/M/1排队系统

A

TP110.74

10.3778/j.issn.1002-8331.1111-0222

HUANG Yewen,WU Hong,WANG Yuanshi.M/M/1 queuing model under non-preemptive limited-priority.Computer Engineering and Applications,2013,49（13）：80-84.

黄业文（1979—），男，讲师，主要研究方向：数理统计，计算机网络与分布计算，模式识别；吴红（1966—），女，副教授；王远世（1964—），男，副教授。E-mail：yewenh@foxmail.com

2011-11-17

2012-01-13

1002-8331（2013）13-0080-05

CNKI出版日期：2012-04-25http://www.cnki.net/kcms/detail/11.2127.TP.20120425.1721.061.html