Helmholtz方程的楔形基区域分解法

童小红，秦新强

西安理工大学 理学院，西安 710054

Helmholtz方程的楔形基区域分解法

童小红，秦新强

西安理工大学 理学院，西安 710054

1 引言

Helmholtz型方程在许多工程领域都会遇到，如电磁场中的波导问题、薄膜振动问题以及海洋工程中水波衍射问题等都是由Helmholtz型方程控制的[1-2]。因此，构造稳定、快速实用的数值算法求解Helmholtz型方程，有着重要的理论和实际意义。

考虑二维Helmholtz型方程的边值问题：

其中，Ω是有界矩形区域，光滑边界∂Ω，Δ为Laplace算子，k为波数。

目前，求解Helmholtz型方程的数值方法有有限元法[3]、有限差分[4]、光谱法[5]。而无网格法是近年来迅速兴起的一种新型、高效的数值方法，基于无网格方法求解偏微分方程的研究也有了一些成果[6-7]。现在国际上常用的处理多元问题的函数基有两种：径向基函数和楔形基函数。基于径向基函数插值求偏微分方程数值解的研究已经有了一系列成果[8-9]，而对于楔形基函数的研究，无论在理论研究方面还是实际应用方面都非常少[10-14]。

但是，使用无网格配点法求解区域较大的问题，当空间步长较小时，节点数的增加会引起系数矩阵的条件数太大，以至于出现病态问题[10，15]。针对这种病态问题，本文引入了楔形基无网格配点的区域分解方法，并应用于求解Helmholtz型方程数值解问题。通过数值算例表明该算法兼有楔形基无网格配点法的优点，降低了系数矩阵的条件数，提高了算法的稳定性，并达到了满意的收敛效果。

2 楔形基配点无网格法

2.1 数值方法的构造

定理1[6]如果ϕ(·)不是多项式，则楔形基{ϕ(cTx+d)}可以逼近几乎所有的函数。

定理2[12]若楔形基函数Ф(x)的傅立叶变换F[Ф](ω)几乎处处大于0，则插值矩阵Q是正定的。

由定理1，设u(x)的近似值u～(x)可以表示为：

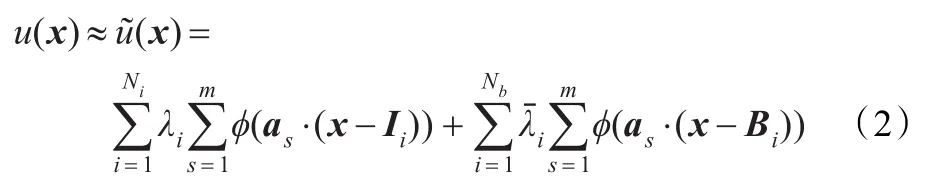
其中，Ii∈W，Bi∈∂Ω，λi为未知系数，Ni表示域内的节点数，Nb表示边界上的节点数，as为固定方向[10]，m为圆盘方向的总组数[10]，ϕ为楔形基函数。

下面，利用楔形基函数作为逼近函数构造无网格方法对问题（1）进行数值求解，离散方案采用配点法。要求式（2）在边界处满足边界条件，在域内满足方程，由（1）可以得到：

当j=1，2，…，(Nb+Ni)时，式（3）和（4）表示的是线性方程组，也就是椭圆型方程的楔形基配点无网格计算方法。为讨论该方法解的存在唯一性，定义矩阵：

其中，A是(Nb+Ni)×(Nb+Ni)矩阵，Λ是待定系数向量，B是给定的右端向量。

2.2 数值解的存在唯一性

定理3[10]函数Ф(x)=ϕ(a·x)是正定函数的充分必要条件是其傅里叶变换F[Ф](w)几乎处处大于零。

定理4如果楔形基函数Ф(x)=ϕ(a·x)是正定的，并且存在，那么AΛ=B存在唯一解。

证明首先证明和存在性。

一般地，取楔形基函数Ф(x)=ϕ(a·x)为偶函数，由定理1和定理3可知，A1是正定的，即存在。

式（6）两边取行列式得：

3 楔形基函数配点区域分解法

假设Ω被分解为两个重叠的区域Ω1和Ω2，记Γ=Ω1∩Ω2≠∅，∂2=∂Ω1∩Ω2，∂1=∂Ω2∩Ω1，如图1所示。

图1 重叠区域图

引理1[16]如果对域Ω1和Ω2的Dirichlet问题皆有解，则对Ω的问题也有解。

由定理4和引理1，得到下面定理：

定理5如果楔形基函数Ф(x)=ϕ(a·x)是正定的，并且存在，那么楔形基函数配点区域分解算法求解Helmholtz型方程（1）存在唯一解。

下面给出求解Helmholtz型方程的楔形基函数配点区域分解算法：

步骤1选初始∈C(∂1)，n:=0。

步骤2在Ω1上采用楔形基函数配点区域分解求解Helmholtz型方程的Dirichlet问题，解得，即

然后，在Ω2上采用楔形基函数配点区域分解求解Helmholtz型方程的Dirichlet问题，解得u～2n+2∈H1(Ω2)，即

步骤3，预先设定的精度为ε0，当εn≤ε0时，结束程序；否则转步骤2。

步骤4置n:=n+1转步骤2。

4 数值算例和分析

算例考虑二维Helmholtz型方程初边值问题：

为了比较楔形基无网格算法的优劣，分别用径向基配点法、有限差分法和有限元法进行计算，结果如图2～5所示。首先，通过图2和图3可以看到楔形基配点法和径向基配点法一样，都能达到满意的收敛效果，其次，将计算时间和计算误差进行了比较，结果如表1。

表1 本文方法与其他数值方法的比较（节点数13×13）

通过表1可以得到结论：楔形基配点法和径向基配点法都能达到较高的精度，得到比较满意的结果；相对于传统的有限差分法和有限元法，本文的楔形基配点无网格方法更有些优势。

将区域Ω分解为Ω1={(x，y)|0≤x≤3/4，0≤y≤1}和Ω2={(x，y)|1/4≤x≤1，0≤y≤1}两个区域，∂1为边x=3/4，∂2为边x=1/4。当ε0=10-6，计算结果如图6～9和表2所示。

通过图6～9和表2，可以看到楔形基配点区域分解法求解Helmholtz型方程切实可行。再通过表2比较发现：楔形基配点区域分解法降低了系数矩阵的条件数，同时降低了计算误差，并达到了满意的收敛效果。

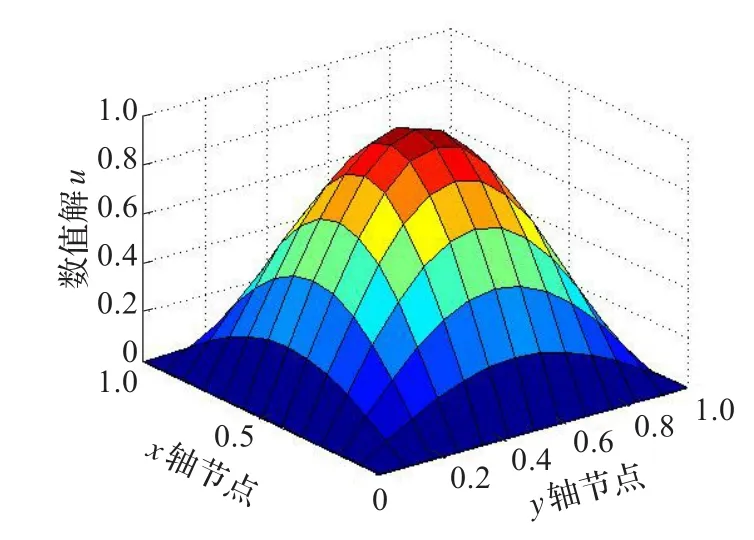
图2 本文的楔形基配点法数值解

图3 径向基配点法数值解

图5 有限元法数值解

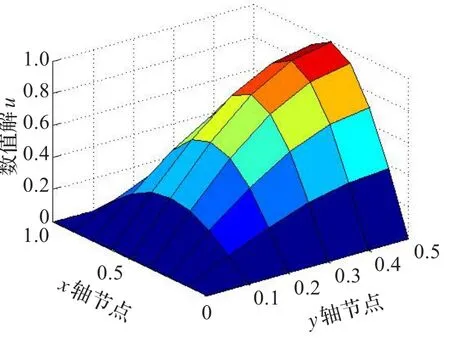
图6 本文区域分解左区域数值解

图7 左区域的误差图

图8 本文区域分解右区域数值解

图9 右区域的误差图

表2 本文数值方法的计算误差和系数矩阵条件数

5 结束语

楔形基配点区域分解法求解Helmholtz型方程切实可行，通过数值算例和分析发现：基于楔形基函数配点区域分解法降低了系数矩阵的条件数，同时降低了计算误差，并达到满意的收敛效果。数值结果表明本文算法具有可行性，能有效地应用于大型区域的工程问题中。

[1]Jin B，Marin L.The plane wave method for inverse problems associated with Helmholtz-type equations[J].Engineering Analysis with Boundary Elements，2008，32（3）：223-240.

[2]Cheng H，Huang J，Leiterman T.An adaptive fast solver for the modifiedHelmholtzequationintwodimensions[J].Journal of Computational Physics，2006，211（2）：616-637.

[3]Van T，Wood A.A time-domain finite element method for Helmholtzequations[J].JournalofComputationalPhysics，2002，183（2）：486-507.

[4]Lambe L A，Luczak R，Nehrbass J W.A new finite difference method for the Helmholtz equation using symbolic computation[J].International Journal of Computational Engineering Science，2003，4（1）：121-144.

[5]Auteri F，Quartapelle L.Galerkin-legendre spectral method for the 3D Helmholtz equation[J].Journal of Computational Physics，2000，161（2）：454-483.

[6]吴宗敏.径向基函数、散乱数据拟合与无网格偏微分方程数值解[J].工程数学学报，2002，19（2）：1-12.

[7]张雄，宋康祖，陆明万.无网格法研究进展及其应用[J].计算力学学报，2003，20（6）：730-742.

[8]Zhang X，Song K Z，Lu M W，et al.Meshless methods based on collocation with radial basis functions[J].Computational mechanics，2000，26（4）：333-343.

[9]Duan Y，Tan Y.Meshless collocation method based on Dirichlet-Neumann substructure iteration[J].Applied Mathematics and Computation，2005，166（2）：373-384.

[10]Wang Z，Qin X，Wei G，et al.Meshless method with ridge basisfunctions[J].AppliedMathematicsandComputation，2010，217（5）：1870-1886.

[11]Tong X，Qin X.A new meshless method for convection diffusion boundary value problems[J].Chinese Journal of Computational Mechanics，2012，29（5）：716-720.

[12]张立伟.楔形基函数插值及其误差估计[J].复旦学报：自然科学版，2005，44（2）：302-306.

[13]张立伟.有限平面波的线性组合的楔形基函数逼近[J].山东大学学报：理学版，2006，41（6）：89-92.

[14]王志刚，秦新强，党发宁，等.楔形基无网格法解的存在惟一性[J].山东大学学报：理学版，2010，45（2）：44-49.

[15]房保言，王志刚，梁波，等.修正Helmholtz方程的小波配点区域分解法[J].武汉理工大学学报，2010，32（3）：120-123.

[16]吕涛，石济民，林振宝.区域分解算法-偏微分方程数值解新技术[M].北京：科学出版社，1992.

TONG Xiaohong,QIN Xinqiang

School of Sciences,Xi’an University of Technology,Xi’an 710054,China

A meshless collocation method for Helmholtz-type equations is developed,which is based on domain decomposition method and ridge basis function.This method overcomes the ill-conditioned problems caused by much larger condition number of the coefficient matrix when collocation method is used for solving Helmholtz-type equations defined large-scale regions. According to numerical example and analysis,it is seen that the method Helmholtz-type equations slows down the condition number of the coefficient matrix and calculation errors,and can achieve satisfactory results.

Helmholtz-type equations;collocation method;ridge basis function;domain decomposition method

基于楔形基函数和无网格配点法，提出了一种求解Helmholtz型方程区域分解法。该方法克服了在求解大规模问题时用一般的全域配点法所带来的配置矩阵为非对称满阵，且高度病态的问题。通过数值结果表明，该算法在求解Helmholtz型方程降低系数矩阵条件数的同时，也能够降低误差，并达到满意的收敛效果。

Helmholtz型方程；配点法；楔形基函数；区域分解法

A

O225

10.3778/j.issn.1002-8331.1210-0240

TONG Xiaohong,QIN Xinqiang.Domain decomposition method for Helmholtz equations based on ridge basis function. Computer Engineering and Applications,2013,49（13）：40-42.

陕西省自然科学基金（No.2012JM1008）。

童小红（1971—），男，讲师，研究方向：计算机图形学，偏微分方程数值解。E-mail：xiaohtong@163.com

2012-10-24

2012-12-20

1002-8331（2013）13-0040-03

CNKI出版日期：2012-12-26http://www.cnki.net/kcms/detail/11.2127.TP.20121226.1120.006.html