具有BIBO稳定的网络系统随机容错设计

周霞，钟守铭

1.阜阳师范学院 数学与计算科学学院，安徽 阜阳 236037 2.电子科技大学 数学科学学院，成都 611731

具有BIBO稳定的网络系统随机容错设计

周霞1，钟守铭2

1.阜阳师范学院 数学与计算科学学院，安徽 阜阳 236037 2.电子科技大学 数学科学学院，成都 611731

1 引言

网络化系统（networked systems），是指通过网络实现控制系统各元件（传感器、控制器、执行器等）之间信息交换的闭环反馈控制系统[1]。相对于传统的点对点互连控制系统而言，网络化系统具有资源共享，系统布线少，成本低，交互性好，诊断能力高，安装和维护容易，可靠性高等优点，广泛地应用于智能交通、航空航天、电气化运输等领域。这些应用对系统的安全性和可靠性要求很高，控制系统一旦发生故障，将会带来无法估量的危害。但另一方面，由于网络带宽等资源受限，网络化系统中存在网络传输时延，数据丢包、乱序等问题，同时系统运行中还可能存在执行器或传感器等故障，这些因素会引起系统控制性能下降，甚至导致系统不稳定。因此，使其具有容错能力是现代网络化控制系统的本质性能要求，同时网络化控制系统的容错控制及控制器的设计引起了学术界的广泛关注。

目前，针对网络化控制系统的容错控制及控制器的设计方面已有相关研究。文献[2]研究了一类不确定网络化控制系统的完整性和保性能鲁棒容错控制问题；文献[3-5]研究了一类具有Markovian特性的随机时延的网络化控制系统的容错控制问题；文献[6]建立网络化控制系统的随机模型，并研究了该模型在传感器和执行器失效故障情况下系统的随机容错控制问题；文献[7]研究了基于观测器的非线性连续网络控制系统容错控制器设计问题；文献[8-9]研究了一类网络化控制系统的控制器设计问题，在[8]中采用连接权矩阵分解的方法，在[9]中采用了反馈增益矩阵分解的方法；文献[10]研究了具有α-稳定的网络化控制系统的容错控制器设计问题；文献[11]研究了一类含有随机扰动的网络化控制系统，具有均方BIBO稳定控制器的设计问题。

以上的研究工作主要是针对网络化控制系统的一般容错控制问题，通过引入0、1常数开关矩阵来实现传感器失效故障、控制器失效故障控制。而事实上，这些元器件的失效故障具有随机性[5]，因此可以引入Bernoulli随机变量序列作为开关矩阵更精确，从而需要研究网络化控制系统的随机容错控制问题。另一方面，在实际问题中，往往还需要追踪到系统的输入信号，对系统的有界输入和有界输出（BIBO）稳定性研究也很有意义，参见文献[11-14]。基于以上讨论，本文将研究具有均方BIBO稳定的网络化控制系统的随机容错控制问题，给出系统存在传感器失效故障和执行器失效故障两种情况下的均方BIBO稳定性条件，及基于该条件下控制器的设计问题。

2 系统的描述和预备工作

考虑网络诱导时延，数据丢包及错序等非理想网络状况因素的单回路网络控制系统，其结构如图1所示。

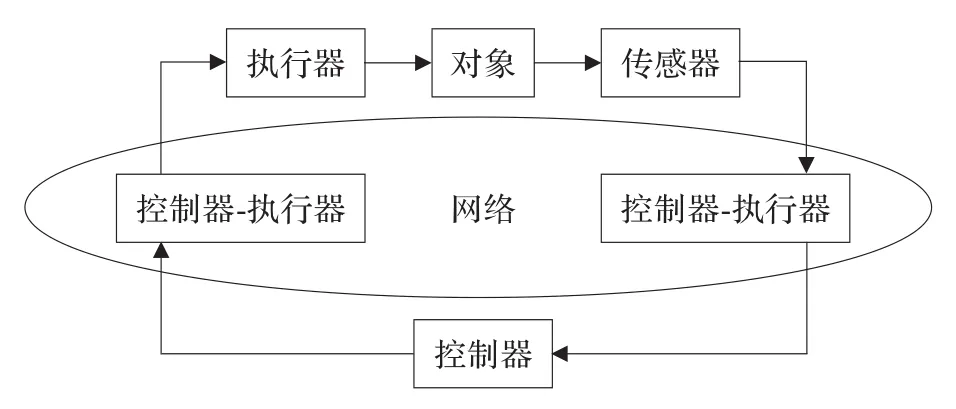
图1 网络化控制系统结构图

假定被控对象为：

其中，x(k)∈Rn为系统的状态变量，u(k)∈Rm为系统控制输入变量，y(k)∈Rl为控制输出变量，A、B、C为合适维数常数矩阵。为了追踪到系统（1）的控制输入，状态反馈控制规律设计为：

其中，K为控制增益矩阵，r(k)为相应的输入向量，τ(k)为传感器到控制器的网络时延τsa(k)与控制器到执行器的网络时延为τca(k)的和，即τ(k)=τsa(k)+τca(k)。则τ(k)为时变时延，且满足：

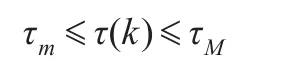
其中τm为网络时延的下界，τM为网络时延的上界。则闭环控制系统（1）可以写为：

为了进一步讨论的需要，引入如下的定义、引理和假设。

定义1[11]向量函数称为的元素，如果满足，其中‖·‖表示Rm空间中Euclid范数或者矩阵范数，N[0，+∞)=[0，1，2，…)。

定义2[11]网络控制系统（1）是均方BIBO稳定的，如果控制器设计为（2）的形式，控制输出y(k)满足：

其中N1、N2是正常数。

引理1[15]对任意的实向量νi∈Rn，i∈N+，有：

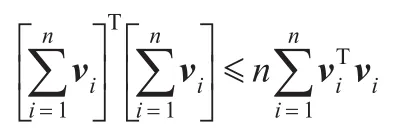
引理2[11]对任意的实向量x、y和合适维数的正定矩阵Q，有：

假设1传感器采用时间驱动，执行器和控制器都采用事件驱动。

假设2传感器与执行器的失效故障与网络状态变量相互独立。

假设3传感器之间、执行器之间及传感器与执行器之间的失效故障相互独立。

3 具有均方BIBO稳定的网络化系统的随机容错设计

情况1传感器存在失效故障情况

在传感器存在失效故障情况下，引入随机开关矩阵序列F(k)，并把它放在反馈增益矩阵和状态变量x(k)之间：

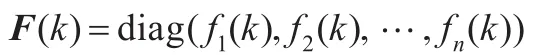
其中，{fi(k)}是一组相互独立的Bernoulli随机变量序列，fi(k)=1表示第i个传感器正常，fi(k)=0表示第i个传感器失效。其概率分布为：，且F可逆。

当系统存在传感器失效故障时，闭环系统（3）可改写为：

基于式（7），可以得到如下定理。

定理1存在状态反馈控制律（2）的随机系统（7）是均方BIBO稳定，若存在实数ρ＞0，正定对称矩阵P、Q、R使得下列矩阵不等式成立：

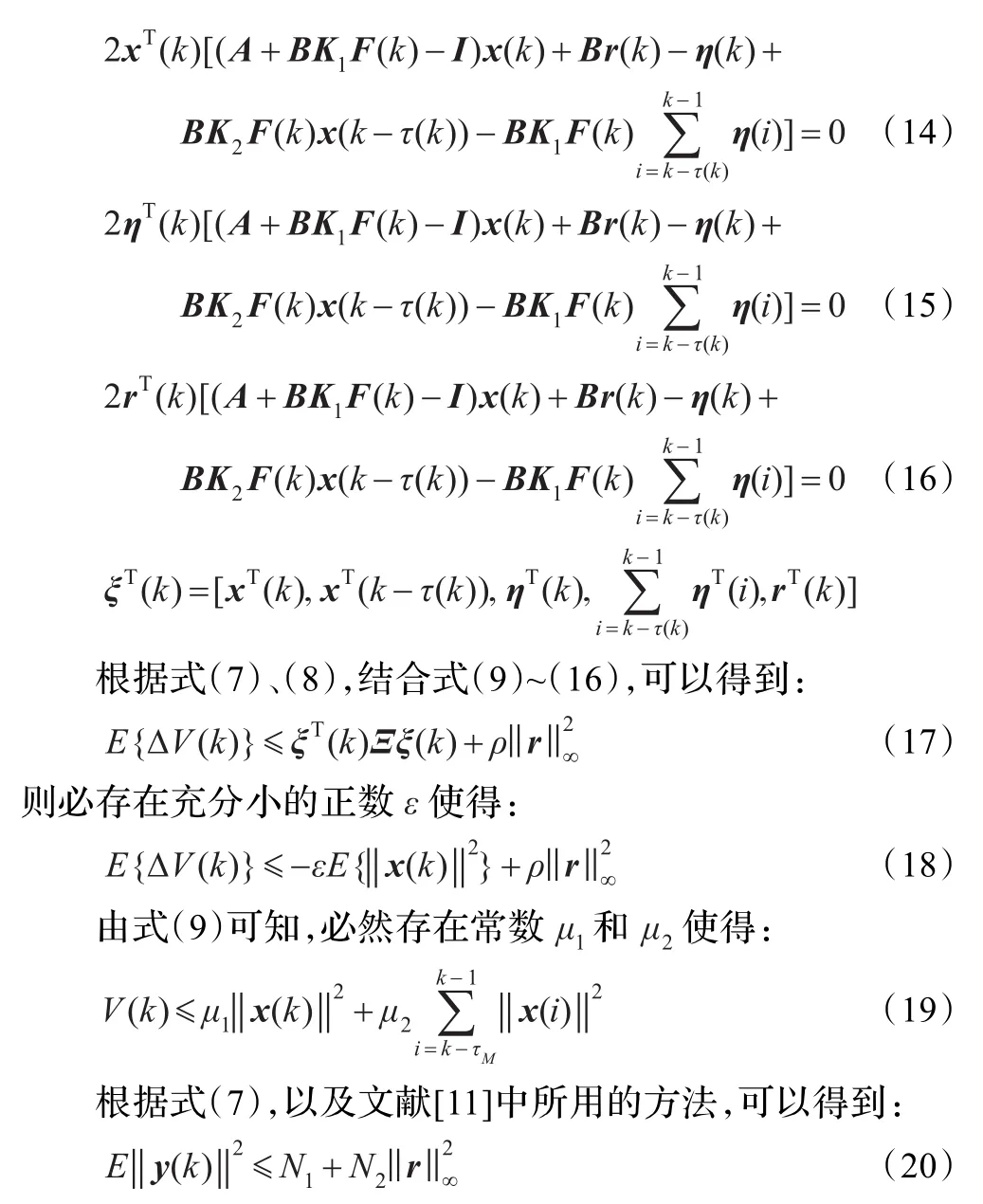
其中，N1、N2为常数。根据定义2可知，具有反馈控制律（2）的网络化系统（7）是均方BIBO稳定的。证明完毕。

注1 由于定理1的条件中出现非线性项，不能通过LMI工具箱直接求出反馈增益矩阵，所以有下面定理。

定理2存在状态反馈控制律（2）的随机系统（7）是均方BIBO稳定，设，如果对任意的正实数ε1、ε2、ε3，若存在正定对称矩阵P、Q、R使得下列矩阵不等式成立：

注2在定理2中，K2的设计有一定的保守性，K1的求解需要通过根据线性矩阵不等式（21）先求出P之后才可以得到。下面试图给出K=K1+K2的任意分解，并且K1、K2的求解可以直接通过LMI工具箱求解。得到如下定理。

定理3存在状态反馈控制律（2）的随机系统（7）是均方BIBO稳定，对任意的对称正定矩阵N、Φ，若存在对称正定矩阵Q、R使得下面线性矩阵不等式成立：

其余的过程证明方法同定理1，这里不再赘述。证明完毕。

注3在定理3中的式（22）中，可以通过LMI不等式直接求解出K1、K2，从而得到控制反馈增益矩阵K。此方法得到的均方BIBO稳定性条件保守性低，自由矩阵少，K的分解也是任意分解。

情况2执行器存在失效故障情况

在传感器存在失效故障情况下，引入随机开关矩阵序列L(k)，并把它放在连接权矩阵和状态反馈矩阵之间：

其中，{li(k)}是一组相互独立的Bernoulli随机变量序列，li(k)=1表示第i个执行器正常，li(k)=0表示第i个执行器失效。其概率分布为：，且L可逆。

当系统存在执行器失效故障时，闭环系统（3）可改写为：

类似于定理1和定理2，针对系统（24）可以得到相应定理，这里不再阐述。在此，只给出类似定理3的相关结论。

定理4存在状态反馈控制律（2）的随机系统（24）是均方BIBO稳定，对任意的对称正定矩阵、，若存在对称正定矩阵、使得下面线性矩阵不等式成立：

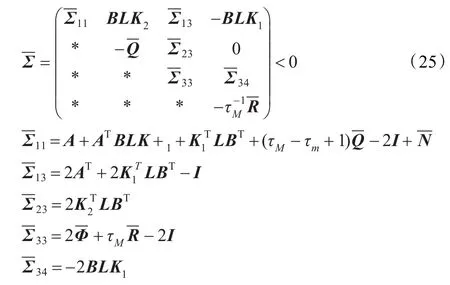
情况3当传感器和执行器同时存在失效故障情况

如同情况1和情况2，引入随机开关矩阵序列F(k)，L(k)，则闭环系统（3）改写为：

由于F(k)，L(k)，x(k)的相互独立性，类似于定理3和定理4，可得下面定理。

定理5存在状态反馈控制律（2）的随机系统（26）是均方BIBO稳定，对任意的对称正定矩阵、，若存在对称正定矩阵、使得下面线性矩阵不等式成立：

4 数值实例

考虑离散化网络控制系统（1），其参数矩阵为：

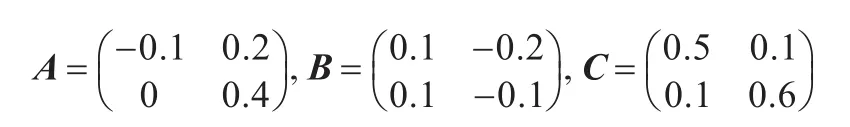
首先，考虑控制系统只存在传感器失效故障情况，并假定传感器的失效概率数学期望矩阵为：

取τm=1，τM=9，由定理3，利用Matlab LMI工具箱可以解得可行解为：

其次，考虑控制系统只存在执行器失效故障情况，并假定执行器的失效概率数学期望矩阵为：

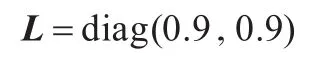
取τm=1，τM=9，由定理4，利用Matlab LMI工具箱可以解得可行解为：

最后，考虑控制系统同时存在传感器和执行器失效故障情况，并假定传感器失效概率数学期望矩阵和执行器的失效概率数学期望矩阵分别为：

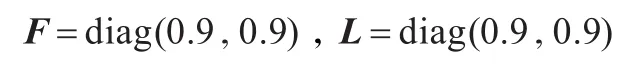
取τm=1，τM=9，由定理5，利用Matlab LMI工具箱可以解得可行解为：

5 结束语

本文就离散时间网络化系统在均方BIBO稳定条件下，系统的随机容错控制和反馈增益矩阵的设计问题进行了研究。通过引入相互独立的Bernoulli随机变量序列作为传感器、执行器失效故障的开关矩阵，研究了在传感器失效故障情况下和执行器失效故障情况下，以及二者同时失效故障情况下的系统均方BIBO稳定条件，并基于此条件给出了反馈增益矩阵的设计。文中定理1和定理2给出的稳定性条件都需要通过对反馈增益矩阵进行设定，通过求解出自由矩阵之后才可以得到反馈增益矩阵，而定理3、4、5可以通过LMI工具箱直接进行求解，并得到反馈增益矩阵的任意分解。数值实例结果表明，本文的结论是有效的。

[1]邱丽.基于Markov跳变理论的网络控制系统研究[D].广州：华南理工大学，2011.

[2]李炜，李亚洁.不确定网络化控制系统的保性能鲁棒容错控制[J].系统仿真学报，2009，21（23）：7544-7548.

[3]霍志红，方华京.一类随机时延网络化控制系统的容错控制研究[J].信息与控制，2006，35（5）：584-587.

[4]Huang D，Nguang S K.Robust fault estimator design for uncertain networked control systems with random time delays：an LMI approach[J].Information Sciences，2010，180（3）：456-480.

[5]Yang C，Guan Z，Huang J.Stochastic fault tolerant control of networked control systems[J].Journal of the Franklin Institute，2009，346（10）：1006-1020.

[6]刘自鑫，钟守铭.网络化控制系统随机容错控制[J].电子科技大学学报，2011，40（4）：549-553.

[7]王燕锋，井元伟，张嗣瀛.基于观测器的非线性网络控制系统容错控制[J].控制理论与应用，2012，29（10）：1348-1352.

[8]刘自鑫，吕恕，钟守铭，等.网络化系统控制器设计的矩阵分解法[J].计算机工程与应用，2010，46（4）：18-21.

[9]刘自鑫，吕恕，钟守铭，等.一类网络化系统控制器设计新方法[J].微电子学与计算机，2010，27（12）：15-21.

[10]李炜，申富媛，曹慧超.具有α-稳定的网络化控制系统容错设计[J].兰州理工大学学报，2011，27（2）：73-79.

[11]周霞，一类网络化随机控制系统的均方BIBO稳定[J].阜阳师范学院学报，2012，29（1）：14-17.

[12]Zhou X，Zhong S.Riccati equations and delay-dependent BIBO stabilization of stochastic systems with mixed delays and nonlinearperturbations[J].AdvancesinDifferenceEquations，2010，Article ID 494607：1-14.

[13]Li P，Zhong S.BIBO stabilization of piecewise switched linear systems with delays and nonlinear perturbations[J].Applied Mathematics and Computation，2009，213（2）：405-410.

[14]Fu Y，Liao X.BIBO stabilization of stochastic delay systems with uncertainty[J].IEEE Transactions on Automatic Control，2003，48（1）：133-138.

[15]Lee T，Radovic U.General decentralized stabilization of largescale linear continuous and discrete time-delay systems[J]. International Journal of Control，1987，46（6）：2127-2140.

ZHOU Xia1,ZHONG Shouming2

1.School of Mathematics and Computational Science,Fuyang Teachers College,Fuyang,Anhui 236037,China
2.College of Mathematics Science,University of Electronic Science and Technology of China,Chengdu 611731,China

The problem of stochastic fault-tolerant control and controller design for networked systems with mean square Bounded Input Bounded Output（BIBO）stability are investigated.Considering the random phenomenon of sensor failure and actuator failure,the random sensor failure and actuator failure are modeled as independent Bernoulli random variable sequence.Combined with linear matrix inequality technology and Lyapunov stability theory,by decomposing the feedback gain matrix,the mean square BIBO stability conditions under the system existence of sensor failure and actuator failure are obtained respectively. Based on the stability conditions,random fault-tolerant controller design of the system is given.Finally,the simulation example is given to demonstrate the effectiveness of design method.

networked systems;stochastic fault-tolerant control;Bernoulli random variable sequence;mean square BIBO stability;controller design method

研究了具有均方BIBO稳定的网络化控制系统的随机容错控制及控制器设计问题。针对网络化控制系统的传感器失效故障和执行器失效故障均具有随机性这一现象，将传感器和执行器的故障建模为相互独立的Bernoulli随机变量序列；利用Lyapunov稳定性理论，结合线性矩阵不等式技术，通过对反馈增益矩阵的分解，得到了网络控制系统存在传感器失效故障和执行器失效故障情况下的均方BIBO稳定条件；基于该稳定条件给出了系统随机容错控制器的设计。以数值实例验证了该方法的有效性。

网络化系统；随机容错控制；Bernoulli随机变量序列；均方BIBO稳定；控制器设计

A

TP13

10.3778/j.issn.1002-8331.1303-0203

ZHOU Xia,ZHONG Shouming.Stochastic fault-tolerant design of networked systems with BIBO stability.Computer Engineering and Applications,2013,49（13）：26-30.

国家自然科学基金（No.11226140）；安徽省教育厅自然科学研究项目（No.KJ2013Z267）；阜阳师范学院自然科学基金（No.2012FSKJ08）。

周霞（1981—），女，博士，讲师，主要研究方向：网络控制系统容错控制，随机系统均方BIBO稳定等；钟守铭，教授，博士生导师，主要研究领域：动力系统及定性理论。E-mail：zhouxia44185@163.com

2013-02-26

2013-04-16

1002-8331（2013）13-0026-05

CNKI出版日期：2013-04-27http://www.cnki.net/kcms/detail/11.2127.TP.20130427.1412.005.html

◎理论研究、研发设计◎