新的直觉模糊熵公式及其应用

沈小雪，郭嗣琮

辽宁工程技术大学理学院，辽宁阜新 123000

新的直觉模糊熵公式及其应用

沈小雪，郭嗣琮

辽宁工程技术大学理学院，辽宁阜新 123000

1 引言

在模糊集理论诞生的初期，模糊熵就作为一种重要的模糊信息度量被引入，并广泛应用在模式识别、图像处理、神经网络等领域。随着模糊集概念的拓展，熵理论的应用也延伸到更多的领域。

模糊集熵的公理化定义是由De Luca和Termini在1972年给出的[1]，1986年，保加利亚学者Atanassov提出了直觉模糊集的概念[2-3]，拓展了传统的模糊集。其后，Gau等人提出了Vague集的概念[4]，Bustince H和Burillo P证明了这两个概念在本质上是相同的[5]，并最早提出了直觉模糊集的模糊熵的公理化定义[6]。拓展的直觉模糊集模糊熵及相关理论的研究引起人们的兴趣，大批学者对直觉模糊集和Vague集的模糊熵开展了深入探究。

由于Burillo P和Bustince H给出的直觉模糊集熵的定义与模糊集熵之间不具有相容性，2001年E.Szmidt和J.Kacprzyk[7]提出了另一种直觉模糊集合熵的公理化定义，并且给出模糊熵的计算公式。李凡等人在文献[8]中指出任意的Vague集的模糊熵可以用其对应的Fuzzy集的模糊熵来表示，但是，黄国顺等在文献[9]中指出了文献[8]的不足之处，考虑了影响Vague集模糊熵的两个因素，提出一个基于非模糊集的Vague集模糊熵公理化定义，给出一个该类熵的计算公式。其后，许多人在前人研究的基础上进一步修正了Vague集模糊熵的公理化定义，用真假隶属度的差异来反映Vague本身具有的模糊性，并相应得到新的模糊熵[10-19]。吕印超等在文献[20]中指出直觉模糊熵应同时反映模糊性和不确定性两方面的影响，提出了模糊度定义，并给出新的修改后的公理化定义，给出直觉模糊熵的一般形式，讨论了模糊熵与测度之间的关系。吴涛等人在文献[21]中指出文献[20]中公理化定义的不合理处，提出新的公理化定义，并且给出新的直觉模糊熵的计算公式。在文献[21]的基础上，文献[22]提出了基于直觉模糊熵的多属性直觉模糊决策问题。

然而，本文通过实例发现文献[21]中直觉模糊熵计算公式仍存在不合理之处，进而给出新的直觉模糊熵的计算公式，并证明新的计算公式符合文献[21]中提出的直觉模糊熵公理化定义，并且把直觉模糊熵转化为权重应用到模糊推理中。

2 基础知识

定义2.1[2]（直觉模糊集）设X是一个给定的有限论域，则X上的一个直觉模糊集A为：

用P(X)和F(X)分别表示X上所有普通集合和模糊集合全体，IFS(X)表示X上所有直觉模糊集全体。

在上述定义中，若∀x∈X，都有μA(x)+νA(x)=1，则直觉模糊集退化为模糊集。对于给定的x∈X，称

为A中x的直觉指数，π(x)为元素x属于A的犹豫度或不确定度。它是x对A的犹豫程度的一种测量，表示“非此非彼”的中立状态。

X中x属于A的隶属度和非隶属度所组成的有序数对：

称为直觉模糊数[23]。

定义2.2[20]（模糊度）称：

为x在A中的模糊度。

在直觉模糊集中，隶属度和非隶属度从不同侧面反映了集合元素的模糊性，而犹豫度反映了集合元素的不确定性。因而，直觉模糊集的熵应该综合反映模糊性和不确定性这两个方面的性质。

3 现有直觉模糊熵的不足

Burillo P和Bustince H给出的直觉模糊集的模糊熵的公理化定义主要考虑了直觉模糊集的不确定性，忽略了直觉模糊集的模糊性，当直觉模糊集退化为模糊集时，该定义与模糊集熵的定义不一致，因而，Szmidt E和Kacprzyk J于2001年提出了直觉模糊熵的新的公理化定义。

定义3.1[7]称映射E：IFS(X)→R+为IFS(X)上的熵，如果E满足下列条件：

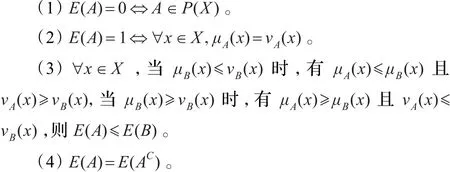
但是，不难发现，在该定义中，直觉模糊熵主要考虑了直觉模糊集的模糊性，但又忽略了直觉模糊集的不确定性。

文献[20]同时考虑了直觉模糊集的不确定性和模糊性，对定义3.1中条件（3）进行补充，将其修改为：

但是，不难看出上述式子仍存在缺陷，例如A1=＜0.3,0.1＞，A2=＜0.3,0.2＞，由公式（2）求得E(A1)=E(A2)= 0.7，显然与直觉也不符合。

4 新的直觉模糊熵公式

从而表明新的直觉模糊熵比文献[21]更符合直觉。

5 直觉模糊推理算法

直觉模糊推理模型为：

步骤1由公式（4），计算出所有直觉模糊数Aij的直觉模糊熵E(Aij)。

步骤2由式（5），求得所有权重ωij。

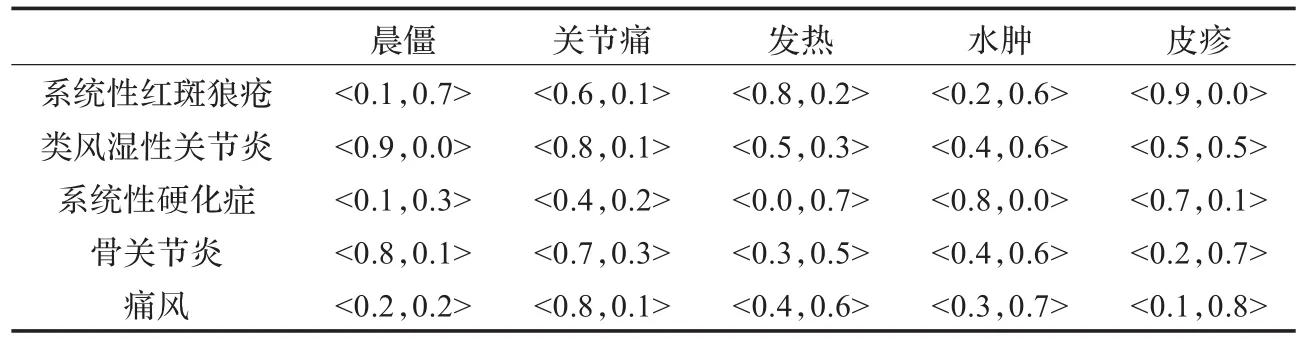
表1 直觉模糊数的病情知识

步骤3利用公式（6），求出给定输入A*与每个直觉模糊推理规则前件Ai(i=1,2,…,n)的加权Hamming距离di=d(A*,Ai)。

步骤4若di=min{d1,d2,…,dn}，则取给定输入A*对应的结论为Bi。

6 实例分析

在疾病诊断中，人们可以通过对“晨僵”、“关节痛”、“发热”、“水肿”、“皮疹”的症状观测，来实现对“系统性红斑狼疮”、“类风湿性关节炎”、“系统性硬化症”、“骨关节炎”和“痛风”这五种疾病的诊断。

为能得出正确的诊断，需要借用在长期临床实践中得到的直觉模糊数表述病情的有关医学知识，即直觉模糊推理规则。这个规则也可以利用一个表给出，如表1。

现有一患者，其关于“晨僵”、“关节痛”、“发热”、“水肿”、“皮疹”的直觉症状为：

7 结束语

本文给出了新的直觉模糊熵的计算公式，并且证明了其符合文献[21]修正的直觉模糊熵的公理定义。进一步根据该直觉模糊熵来确定因素的权重，并将其应用到直觉模糊推理问题中。

[1]De Luca A，Termini S.A definition of a nonprobabilities entropy in the setting of fuzzy set theory[J].Inform and Control，1972，20：301-312.

[2]Atanassov K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，1986，20：87-96.

[3]Atanassov K.More on intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，1989，33（1）：37-46.

[4]Gau W L，Buchrer D J.Vague sets[J].IEEE Trans SMC，1993，23（2）：610-614.

[5]Bustince H，Burillo P.Vague sets are intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems，1996，79（3）：403-405.

[6]Burillo P，Bustince H.Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets[J].Fuzzy Sets and Systems，1996，78（3）：305-316.

[7]Szmidt E，Kacprzyk J.Entropy for intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems，2001，118：467-477.

[8]李凡，吕泽华，蔡立晶.基于Fuzzy集的Vague集的模糊熵[J].华中科技大学学报：自然科学版，2003，31（1）：1-2.

[9]黄国顺，刘云山.关于Vague集的模糊熵[J].计算机工程与应用，2005，41（33）：48-50.

[10]牛彩云，杨勇，金兰.一种新的直觉模糊集的熵[J].计算机工程与应用，2009，45（34）：32-34.

[11]王毅，雷英杰.一种直觉模糊熵的构造方法[J].控制与决策，2007，22（12）：1390-1394.

[12]孙宁宁，余建坤，杨力军.一种新的Vague集的熵[J].计算机工程与应用，2011，47（24）：43-45.

[13]江伟，梁家荣，蒋建兵.新的Vague熵构造方法[J].计算机工程与应用，2008，44（27）：75-77.

[14]王凌云，鲁小云，王治和.Vague集模糊熵的再研究[J].计算机工程与应用，2009，45（30）：31-33.

[15]彭芳艳，梁家荣，伍华健.Vague集模糊熵的新构造方法[J].计算机工程与应用，2009，45（29）：52-54.

[16]朱六兵，杨斌，陈纪东.Vague集模糊熵的构造方法研究[J].模式识别与人工智能，2006，19（4）：481-484.

[17]范平，梁家荣，李天志.Vague集的新模糊熵[J].计算机工程与应用，2007，43（13）：179-181.

[18]李天志，梁家荣，范平，等.Vague集的模糊熵[J].计算机应用研究，2007，24（10）：93-98.

[19]徐凤生.Vague集的模糊熵及其构造[J].计算机工程与应用，2011，47（23）：39-40.

[20]吕印超，郭嗣琮.直觉模糊集的熵及其一般形式[J].计算机工程与应用，2011，47（28）：52-55.

[21]吴涛，白礼虎，刘二宝，等.直觉模糊集新的熵公式及应用[J].计算机工程与应用，2013，49（23）：48-51.

[22]秦华妮，骆达荣.直觉模糊熵与加权决策算法[J].数学的实践与认识，2012，42（4）：255-260.

[23]Xu Z S，Yager R R.Some geometric aggregation operators based on intuitionistic fuzzy sets[J].International Journal of General Systems，2006，35：417-433.

[24]Szmidt E，Kacprzyk J.Distances between intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，2000，114（3）：505-518.

[25]万鑫.模糊推理在急病辅助诊断系统中的应用研究[D].长沙：湖南大学，2009.

SHEN Xiaoxue,GUO Sicong

College of Science,Liaoning Technical University,Fuxin,Liaoning 123000,China

The entropy for intuitionistic fuzzy sets reflects the fuzziness and uncertainty of the intuitionistic fuzzy sets.Therefore, it is extremely significant to put forward the reasonable and right axiomatic definition and calculation formula of the intuitionistic fuzzy sets.The paper points out the irrationality of the calculation formula in the literature by example,and puts forward a new calculation formula of the entropy for intuitionistic fuzzy sets.The proof is given.The weight determined by the entropy for intuitionistic fuzzy sets is applied to the fuzzy reasoning.Accordingly,to solve the practical problems is effective.

intuitionistic fuzzy sets;entropy;weight;fuzzy reasoning

直觉模糊熵反映了直觉模糊集的模糊性和不确定性，因而提出合理正确的直觉模糊熵的公理化定义以及计算公式是十分重要的。通过实例指出已有文献中直觉模糊熵计算公式的不合理，提出新的直觉模糊熵的计算公式，对其进行了证明。根据该直觉模糊熵确定的权重应用到模糊推理过程中，从而有效地解决实际问题。

直觉模糊集；熵；权重；模糊推理

A

TP18

10.3778/j.issn.1002-8331.1305-0467

SHEN Xiaoxue,GUO Sicong.New entropy formular for intuitionistic fuzzy sets and its application.Computer Engineering and Applications,2013,49（24）：28-31.

教育部高校博士学科点专项科研基金（No.20102121110002）。

沈小雪（1988—），女，硕士研究生，研究领域为模糊推理；郭嗣琮（1951—），男，教授，研究领域为模糊分析学、模糊预测与决策等。E-mail：xiaoxue1989314@163.com

2013-06-03

2013-08-19

1002-8331（2013）24-0028-04

CNKI出版日期：2013-10-11http://www.cnki.net/kcms/detail/11.2127.TP.20131011.1653.001.html