基于协同PSO算法的非均匀采样系统辨识

王涛，林卫星，包建孟

宁波大学信息科学与工程学院，浙江宁波 315211

基于协同PSO算法的非均匀采样系统辨识

王涛，林卫星，包建孟

宁波大学信息科学与工程学院，浙江宁波 315211

1 引言

多率系统（Multirate system）是指存在两种及两种以上操作频率的系统，它在石油、化工、冶金等工业过程控制方面得到广泛的应用。诸如：在复杂设备和生产线中的塔釜、容器和管道等都具有多个控制（测量）点，这些过程不仅采样率不一样，而且可能采样间隔也不均匀，检测数的时间往往较长，而过程控制信号的刷新频率则相对较快，所以传统的控制系统是无法满足工业过程的需要的[1]。对多率系统的研究可以追溯到20世纪50年代，第一个重要工作是Kranc于1957年提出的开关分解技术（Switch decomposition technique），后来由Friedland和Khargoneckar等人发展而引入提升技术（Lifting technique）[2]，它可以将一个周期离散时变系统化为一个时不变系统。现在，提升技术已成为处理多率系统的一个标准工具。在获得非均匀采样数据系统的提升状态空间模型的基础上，进一步将其转化为输入输出表达的传递函数模型，从而应用多种辨识方法进行系统的辨识。目前多率系统的研究已经成为国内外研究的一个热门领域，研究的活动涉及多率系统的系统辨识、鲁棒性研究、预测控制等。但是，值得注意的是，多率系统的数学模型是研究和分析多率系统的基础。近些年来，许多学者也相继提出了一些模型框架，有时域模型（其中包括时变传递函数模型）、有理分式传递函数模型、状态空间模型、频域模型、小波模型还有其他的模型等[3]。

PSO算法是由美国学者Kennedy和Eberhart于1995年提出的一种模拟鸟群觅食寻优算法。由于PSO算法可用于解决非线性、不可微和多峰值复杂函数的优化问题。与其他进化算法相比，它有着思想简单、容易实现、可调参数较少和应用效果明显等优点，所以得到了广泛的研究和应用[4]。本文提出将改进的PSO算法应用在双率系统的参数辨识问题上，与传统的多率辨识方法进行比较、分析来证明该算法的有效性和优越性。

2 系统描述

2.1 非均匀采样多率系统

在一类工业过程控制领域中，普遍采用的双率系统（Dual-rate system）如图1所示。其为单输入单输出的离散时间系统，其中控制输入非均匀刷新周期不等于控制输出的非均匀采样周期，就得到了一个简单的非均匀采样多率系统，P表示连续时间过程，v(t)是一个零均值随机白噪声，连续时间过程P的输入u由非均匀零阶保持器HmT生成，P的输出受噪声v(t)的影响，并由非均匀采样器SnT生成输出为y。输入u和输出y是离散时间信号，经过保持器和采样器的作用，输入和输出的周期可视为mT和nT。即使过程P是一个线性时不变过程，由于输入刷新和输出采样周期的不同，从u到y的整个系统也是一个时变系统。为了使这个时变系统易于处理，下面介绍空间提升技术[5]。

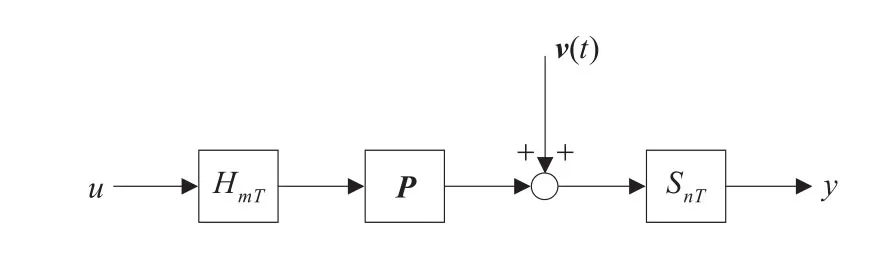
图1 非均匀采样系统

2.2 空间提升技术

假设u(k)是一个离散时间信号，把连续n次输入u(k)放在一起构成一个输入信号序列u(L)，u(k)到u(L)的映射关系可以表示为式（1）、式（2）所示。

虽然提升后u(L)的刷新周期是原信号u的n倍，但是提升信号u的维数也提高为原信号u的n倍，因此原有的系统信息并没有因为刷新周期的变化而遗失[6]。同样，对输出采样信号通过Lm进行提升得到y，对噪声信号v通过Lm进行提升得到v，原双率采样系统通过提升技术获得框架周期为mnT的单率采样系统，如图2所示。

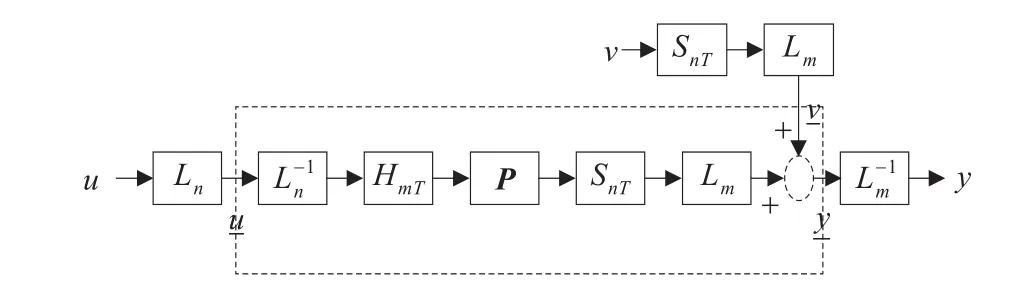
图2 提升的双率采样系统

提升后，得到一个离散时间线性单率系统，如公式（3）所示。系统提升后的状态空间模型如式（5）、式（6）所示。

式中，k=0表示采用输出误差结构，-v为一个白噪声向量，x是状态向量[7-8]。假设P(z)的秩为p，则A，B，C，D的维数可以表示为p×p，p×1，1×p，1×1，而的维数可以表示为p×p，p×n，m×p，m×n。

2.3 传递函数转换

已知一提升状态空间方程如式（8）所示。

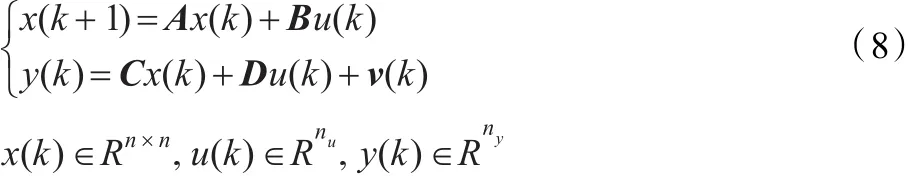
其中，离散时间变量k为一个正整数。通过Z变换得式（9）所示。

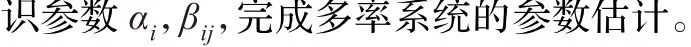
3 改进协同PSO

3.1 标准PSO

PSO算法首先在解空间中初始化一群粒子，用位置、速度、适应度值三项指标来表示粒子的特性。适应度是由适应度函数计算得到的，其值的好坏代表粒子的优劣。粒子在空间中运动，通过跟踪个体极值Pbest和群体极值Gbest来更新位置，并且通过比较新粒子的适应度值和群体极值的适应度值来更新个体极值Pbest和群体极值Gbest[11]。

现假设在一个D维的空间里，有n个粒子组成的种群X=(X1,X2,…,Xn)，其中Xi=(xi1,xi2,…,xiD)，代表第i个粒子在D维空间中的位置，根据目标函数即可计算出粒子在位置Xi的适应度值。第i个粒子的速度为Vi=(Vi1,Vi2,…,ViD)T，其个体极值为Pi=(Pi1,Pi2,…,PiD)T，种群的全局极值为Pg=(Pg1,Pg2,…,PgD)T。每次迭代中，粒子通过个体极值和全局极值来更新自身的速度和位置，更新公式如式（14）、式（15）所示。

式中，w为惯性权重(d=1,2,…,D)，Vid为粒子的速度，c1、c2为非负数常数，r1、r2为分布在[0，1]的随机数，为了防止粒子的盲目搜索，通常会设定其位置速度在一定的区间里[-Xmax,Xmax]，[-Vmax,Vmax]。

与遗传算法相比，粒子群优化算法操作和实现都比较简单，保留了基于种群的全局搜索策略，省略了遗传算法中的交叉和变异操作。其比较独特地利用了本身最优信息和群体最优信息来搜索当前区域，是一种高效的概率搜索算法，已经列入“国际进化计算会议”的专题讨论之一[12-13]。

3.2 协同PSO

PSO具有收敛速度快和通用性强的特点，但是同时存在着容易早熟的缺点，这时就丧失了种群多样性[14]。另一方面，在粒子更新公式（14）、公式（15）中，只有种群的最优值和个体最优值被粒子应用，这也是造成早熟收敛的另一原因[15]。为了避免早熟收敛，充分利用所有粒子的信息，设置早熟判定器。当早期粒子陷入局部极值点时，用扰动来跳出这个早熟点。本文利用群体生物的协作行为特点，在粒子更新公式中加入其他粒子的搜索结果，并加入基于阈值的早熟判定因子，在检测到早熟时加入交叉变异扰动种群，以改善粒子群优化算法的搜索性能。

3.2.1 粒子协同机制算法

3.2.2 算法收敛性分析

公式（16）中，主要通过四部分来更新粒子速度：第一部分参考粒子前一时刻的一定比例速度；第二部分以粒子当前位置和自己最好位置之间的距离为依据，向个体最优值靠近；第三部分是粒子的当前位置和群体最优位置之间的距离，表现群体知识的共享和合作；第四部分为粒子当代所有粒子的平均位置和粒子的当前位置之间的距离为依据，取平均值，更能客观反映大多数粒子的位置范围，指示粒子以一定的概率追随大多数粒子的位置所在，往大多粒子聚集的地方靠拢，可以更加快捷，准确地找到群体的最优值，有效避免陷入局部峰值的现象。

可以看到，方程（19）为标准的离散线性状态方程，则状态变量的离散状态方程的特征方程为：λ2+(φ-1-w)·λ+w=0。

经过上述分析化简可得，CPSO算法的系统特征方程化简形式仍与标准PSO保持一致，根据系统稳定性理论，当G的所有特征值幅值都小于1时，系统稳定，文献[12]已有详细证明。说明了新的算法和标准PSO具有相同的收敛特性，本算法在加入平均变异扰动后，只是对历史搜索的最优值进行扰动变异，增强了算法的鲁棒性，使粒子更易逃出局部最优，更快地达到更好的最优点。

3.2.3 阈值自判断机制

当粒子陷入局部最优时，粒子的迭代过程中全局最优解Gbest不再变化或者变化很小。由此可设置一个基于阈值的早熟检测方法。当Gbest在连续迭代中更新很小或不更新，检测计数num加1，当num≥Tm（Tm是连续Gbest的变化不超过阈值的迭代次数）时，判定群体搜索处于局部最优。

3.2.4 随机交叉和变异

3.2.5 算法流程

步骤1初始化最大迭代代数，种群规模N，粒子维数D，迭代代数计数器num，早熟阈值Q，迭代次数阀值Tm，c1=c2=2。

4.2.3 出口创汇的发展。胶州大白菜在国内市场不断增长，同时又销往日韩、欧美等国家，在全球市场上得到广泛认可。2016年，胶州大白菜的国内市场占其销量的74.12%，国外市场占25.88%。其中，日、韩成为胶州大白菜国外的主要市场，韩国约占18.31%，日本占其销量的6.16%。

步骤2根据公式（17）、公式（18）更新粒子速度和位置，如溢出取上下限值。

步骤3计算每个粒子适应度值Jh。

步骤4比较Jh、Pbest、Gbest，更新粒子最优位置。

步骤5判断ΔGbest，若ΔGbest≤Q，num++，当num≥Tm时，转到式（16）进行更新粒子位置。

步骤6判断算法是否满足终止条件，若满足转向步骤7，否则转向步骤3。

步骤7输出粒子的相关信息，算法结束。

4 实验验证

4.1 状态空间模型辨识

取p=3，刷新和采样时间间隔依次为τ1=1 s，τ2=2 s，τ3=3 s，刷新和采样时间点为t1=1 s，t2=3 s，框架周期t3=T=τ1+τ2+τ3=6 s。提升状态空间模型如式（21）所示。

为验证上述改进算法的有效性，分别研究了系统在白噪声和有色噪声干扰情况下的用MATLAB软件设计实现的数字仿真，仿真对象如式（20）所示。

当系统的输入为零均值的单位方差随机信号序列，{v(kT)}采用零均值方差为的白噪声序列，取σr=0.1，其

其中，h为数据宽度，λ为遗忘因子且λ∈[0,1]，i越大，λi就越小，以提高数据的权重，更好地跟踪系统。系统实际输出Y(k)、估计输出Yˆ(k)。定义误差率为δ=||θ′-θ||/||θ||,(||X||= XTX)为参数估计误差，θ为真值参数构成的向量，θ′为θ的估计。采用本文提出的协同粒子群算法辨识对应的可观测性空间状态模型如式（23）所示。适应度函数如式（22）。

误差估计曲线如图3示，表1给出了运用CPSO得到的参数估计、真值和系统的相对的误差率值。最后辨识得到的提升多率系统的空间状态模型如式（24）所示。

图3 CPSO参数误差随k的变化曲线

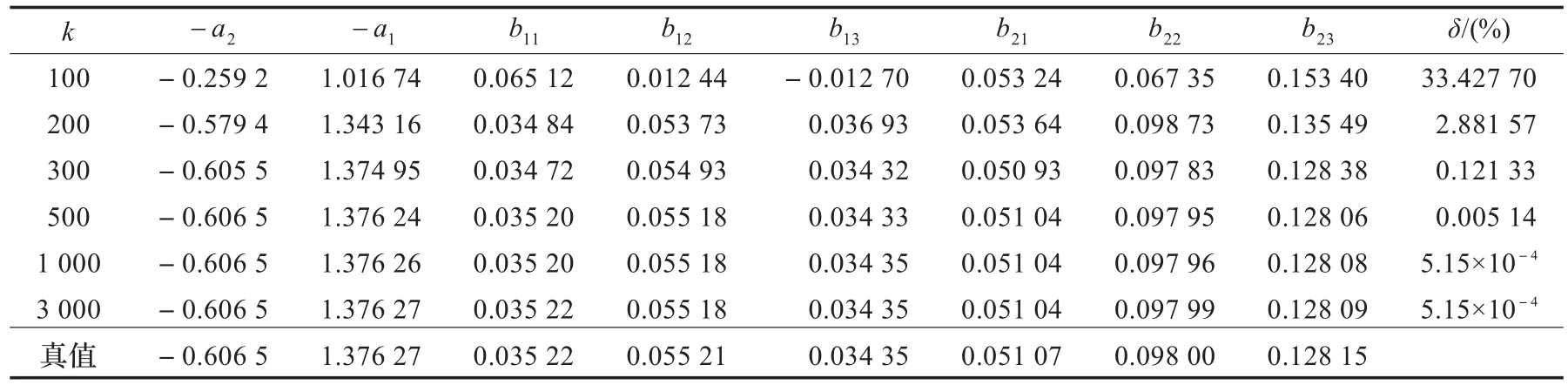
表1 CPSO的真值与参数估计(σr=0.1)

表2 随机梯度法真值与参数估计(σr=0.1)

随机梯度法得到的实验数据如表2所示[16]。

从表1和表2的数据对比中，可以看到，对含有白噪声干扰的非均匀采样系统。引入变异因子的协同CPSO算法在迭代次数200次的时候系统误差率2.881%远远优于随机梯度算法的42.94%，几乎已经达到随机算法在3 000次时误差率1.797 5%收敛效果。迭代3次时，CPSO算法收敛精度为5.15×10－4%，随机算法收敛在1.797%，精度倍数约104个数量级。图3研究了CPSO在白噪声干扰下系统的收敛过程。从图中可以看出，在前300次迭代时没有引入变异因子，系统收敛速度比较快。在500次时，系统收敛速度缓慢，误差率几乎为零，系统平稳，达到很好的收敛效果。

4.2 传递函数模型辨识

现假设当系统的输入为零均值的单位方差随机信号序列，{v(kT)}采用零均值方差的有色噪声信号，取σr= 0.1时，则得到系统提升的传递函数模型如式（25）所示。

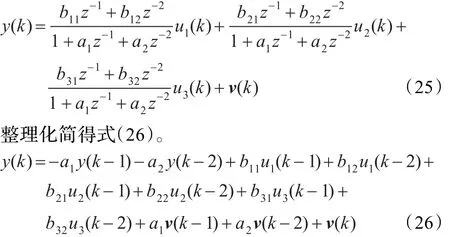
其中，a1v(k-1)+a2v(k-2)+v(k)为一有色噪声序法辨识在有色噪声(σr=0.1)干扰下时的参数估计，如表3所示。各算法的误差跟踪曲线如图4所示。为了更好研究CPSO算法的鲁棒性，定义噪信比为噪声幅值与信号幅值之比，分别取噪信比为0.1、0.5、2时系统的参数估计如表4，误差曲线如图5所示。

表3 有色噪声下参数真值和参数估计(σr=0.1)

图4 有色噪声下各算法的误差变化曲线(σr=0.1)

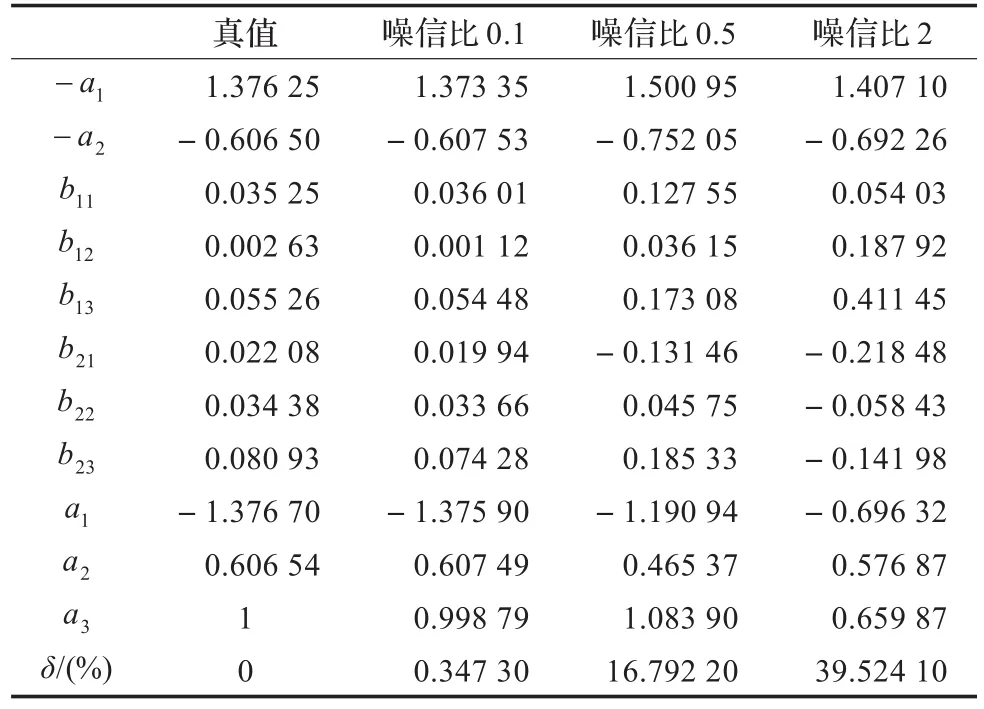
表4 CPSO在不同噪信比噪声下的辨识值

图5 不同有色噪信比下的CPSO算法的误差曲线

从表3得出各算法在有色噪声(σr=0.1)干扰下系统的收敛情况。CPSO收敛误差率为0.347 3%、SPSO为33.150 5%、递推LS为81.548 4%。CPSO参数辨识的精度最高。表4实验数据是将噪声扰动依次提高的结果，噪信比分别为0.1、0.5、2时，CPSO算法的收敛在误差率分别为0.347 3%、16.792 9%、39.524 1%。图4研究了在有色噪声干扰下，三种算法的收敛性能的比较。从图中可以看出，SPSO和LS算法收敛速度很快但是精度不高。CPSO虽然收敛速度稍慢，但是保持了很高精度，能够准确估计到参数真实值。图5是依次取噪信比0.1、0.5、2，曲线仍然可以收敛，表明CPSO算法无论从精度还是鲁棒性都优于其他几种算法，较好地克服了SPSO易陷入局部收敛的缺点。

5 结论

本文针对非均匀采样的多率系统的输入和输出数据，采用提升技术，提出了基于新型的协同粒子群优化的辨识算法，通过在白噪声干扰下的空间状态方程模型和有色噪声干扰下的差分模型的参数辨识，对比传统的辨识算法，新型的协同算法在参数精确度、鲁棒性和实时性上都得到较好的结果，从而证明了该算法的合理性和有效性。

[1]倪博溢，萧德云.多采样率系统的辨识问题综述[J].控制理论与应用，2009，26（1）：62-68.

[2]Ding F，Chen T.Modeling and identification for multirate systems[J].Acta Automation Sinica，2005，31（1）：105-122.

[3]宋广雷，陈晓明，丁峰.基于双率采样数据的动态调节系统的辨识[J].科学工程，2010，10（35）：8831-8833.

[4]Zhu Y，Telkamp H，Wang J H，et al.System identification using slow and irregular output samples[J].Journal of Process Control，2009，19（1）：58-67.

[5]刘建华，刘国买，杨荣华，等.粒子群算法的交互性和随机性分析[J].自动化学报，2012，38（9）：1471-1484.

[6]丁峰，陈通文，萧德云.一般双率随机系统状态空间模型及其辨识[J].自动化学报，2004，30（5）：652-661.

[7]吴晓军，李峰，马悦，等.均匀搜索粒子群算法的收敛性分析[J].电子学报，2012，40（2）：1117-1120.

[8]方崇智，萧德云.过程辨识[M].北京：清华大学出版社，1988.

[9]丁峰.系统辨识理论与方法[M].北京：电力出版社，2011.

[10]Francis B A，Georgiou T T.Stability theory for linear timeinvariant plants with periodic digital controllers[J].IEEE Trans on Automat Control，1988，33（9）：820-823.

[11]Zhou Y L.Research and application on bacteria foraging optimization algorithm[J].Computer Engineering and Applications，2011，20（46）：16-21.

[12]林卫星，陈炎海.一种快速收敛的改进粒子群算法[J].系统仿真学报，2011，23（11）：2406-2411.

[13]杨志鹏，朱丽莉，袁华.粒子群优化算法研究与发展[J].计算机工程与科学，2007，29（6）：61-64.

[14]罗金炎.连续型粒子群优化算法的均方收敛性分析[J].电子学报，2012，40（7）：1364-1367.

[15]郭冀，彭鑫，马林华.结合文化算法的多种群协同变异PSO算法[J].计算机工程与应用，2011，47（6）：48-49.

[16]丁锋，陈通文，萧德云.非均匀周期采样多率系统的一种辨识方法[J].电子学报，2004，32（9）：1414-1420.

WANG Tao,LIN Weixing,BAO Jianmeng

Faculty of Information Science and Technology,Ningbo University,Ningbo,Zhejiang 315211,China

For one type of non-uniformly sampled data of dual-rate system,by using the lifting technique the state space models of the multirate systems are got and thus the corresponding transfer functions are obtained.An asynchronous pattern from analyzing on biologic character of particle swarm optimization is proposed,and a novel method is studied for dual-rate system identification which is based on the improved CPSO（Cooperative Particle Swarm Optimization,CPSO）under different noise models.To prove the validity and rationality of the new algorithm,this paper compares the differences of many traditional algorithms and CPSO algorithm in accuracy and robustness by experimental simulation.

dual-rate system;non-uniformly sampled-data systems;state space model;parameter estimation;cooperative Particle Swarm Optimization（PSO）

对于非均匀采样数据的双率系统，运用提升技术，得到系统离散状态空间模型，变换得到相应的传递函数模型。讨论在有色噪声和白噪声的干扰下，提出了利用协同粒子群（Cooperative Particle Swarm Optimization，CPSO）的新颖算法，通过实验仿真对比传统的算法和协同PSO算法的精度和鲁棒性，证明新型算法的有效性和合理性。

双率系统；非均匀采样系统；状态空间模型；参数估计；协同粒子群优化（PSO）

A

TP271

10.3778/j.issn.1002-8331.1303-0473

WANG Tao,LIN Weixing,BAO Jianmeng.Method of non-uniformly sampled-data system identification based on cooperative PSO.Computer Engineering and Applications,2013,49（24）：32-37.

浙江省教育厅重点项目（No.Z201017236）；浙江省钱江人才项目（No.2011R10074）；宁波市自然科学基金（No.2012A610005）。

王涛（1988—），男，硕士，研究方向为智能算法，信息集成和智能控制；林卫星（1957—），男，教授，研究方向为系统辨识，智能控制与优化，计算机控制；包建孟（1987—），男，硕士，研究方向为信息集成和智能控制与优化。

2013-03-29

2013-06-07

1002-8331（2013）24-0032-06

CNKI出版日期：2013-09-12http://www.cnki.net/kcms/detail/11.2127.TP.20130912.1436.013.html