关于“扇形的面积”的教学指导研究报告

俞宏毓，顾非石

（1．绍兴文理学院 数理信息学院，浙江 绍兴 312000；2．华东师范大学 数学系，上海 200241；3．上海市徐汇区教师进修学院，上海 200231）

1 研究背景

2011年2月，顾泠沅教授组织发起对教师发展指导者工作的研究，并且同美国的Paine Lynn教授、日本的Takashi Nakamura教授等人合作，进行关于教师发展指导者的国际比较研究．教师发展指导者项目的研究，是顾泠沅教授领衔的青浦实验研究的延续，目的是通过对教师发展指导者工作现状的研究，分析其优势和不足，并探索如何提高其自身素养和指导水平，从而使其更好地为促进教师的专业发展服务，同时通过国际比较进行取长补短．和青浦实验以往的做法一样，这次的项目也是从数学学科开始的[1]．2011年 5月下旬，顾泠沅教授组织了一个23人的研究团队，在浙江义乌进行了一周的预研究实验，于9月份在上海市青浦教师进修学院对实验的材料进行了精致化的分析，得出了教师发展指导者工作的分析框架，并在9月底的中、日、美3国会议上进行了交流．（详见文[2]）在该次会议上，三方达成一致，将教师发展者界定为教研员、第一线的专家教师和大学等教育研究机构的课程教学研究人员的总体．

2011年10月起，在顾泠沅教授的号召下，上海市的青浦等区大面积开展各学科、各学段的实验研究．2011年底在青浦实验中学开展的关于“扇形的面积”的教学指导研究活动是其中之一．顾泠沅教授根据自己多年从事教研员工作及教师教育研究的经验，指出教师发展指导的软肋是教学设计的改进．因此对这次“扇形的面积”的教学指导活动，顾泠沅教授提出了一个全新的设计方案，运用行动教育模式验证其有效性．

2 研究过程与方法

2.1 参与人员与研究对象

上海市青浦区实验中学，是一所公办初级中学，其前身是有八十多年历史的青浦中学初中部，现为上海市文明单位，是上海市课程教学改革基地学校．学校每个年级有 14个平行班，班级规模一般在55人左右．

2011年11月下旬开始，青浦教师进修学院宋伟倩等教师、徐汇区教师进修学院科研员顾非石、华东师范大学数学系研究生俞宏毓等 3人以及青浦实验中学的忻映霞等数学教师，在青浦实验中学进行了延续一个月的教学指导研究活动．其中青浦教师进修学院的宋伟倩和肖彩凤作为区域层面的教师发展指导者角色，青浦实验中学的专家教师忻映霞和班丽娜作为学校层面的教师发展指导者的角色．参加活动的执教教师是有6年教龄的男教师宋秦．宋秦老师毕业于上海师范大学的小学教育专业，职称为中教二级．执教的班级是六年级的3个平行班，各班学生基础相当．

2.2 研究材料

执教内容是上海教育出版社的六年级上册“4.4 扇形的面积”．这节课主要是学习扇形面积的两个公式及其应用．在这节课之前，学生已经学习了圆的周长和弧长以及圆的面积．

2.3 研究思路与过程

活动采用顾泠沅教授的“三个关注、两个反思”的行动教育模式，上了3次课，每次课后召开教学指导会议．根据行动教育模式，第一次课是执教教师自己设计的原生态课．指导会议首先由执教教师陈述对教学的看法及教学的得失，然后教师发展指导者点评、提出改进意见．第一次课后的指导会议，教师发展指导者和执教教师根据顾泠沅教授的设计思路，讨论确定第二次上课的教学设计．第二次课后的指导会议，根据设计与学生现实的差距，重在教学行为上的改进．

3次课都进行了前后测试，测试题由顾泠沅教授亲自设计，其中后测分两次进行，分别考察学生应用扇形面积公式的能力和公式推导能力（见附录）．活动中分别对教师发展指导者、执教教师和学生进行了深度访谈，每次访谈都进行了录音．

活动的课堂和会议都进行了全程录像，并转化成了文本，运用录像带分析法进行分析．首先对课堂教学的整体结构进行研究，展现执教教师3次课教学的异同，分析其进步的历程．然后通过对3次课测试结果的比较，分析教学效果的差异，并结合访谈的结果，验证新设计思路的有效性．

3 新设计基本思路

顾泠沅教授的新设计思路是通过复习推导圆面积公式的分割和拼接过程，引导得出如图1），然后由部分与整体关系得出两个公式的一致性．为帮助学生对公式进行相互推导，还借助另外一个公式公式②），这个公式也可以由部分与整体关系得出．由公式②推出公式③相对比较直接．在课堂上，这3个公式可以让学生通过探究得出．

练习的设计安排，除公式应用的常规题之外，最后设计了一个拓展题，让学生思考如何求图2所示扇环的面积．

图1 圆面积公式推导

图2 求扇环面积

4 三次教学情况比较分析

4.1 整体结构比较

4.1.1 基本教学流程概观

第一、三次课的整体结构如图3所示．第二次课除了让学生通过特殊角的扇形来探究面积公式外，其它环节与第三次课基本一致．

4.1.2 三次课教学用时分布3次课教学用时分布如表1所示．

图3 第一和第三次课的整体结构

表1 3次课教学用时分布

4.1.3 主要变化

通过对3节课教学流程的概括和3次课教学用时分布可以看出，执教教师在活动过程中对同一内容的3次执教行为发生了很大变化．这里仅分析4个比较显著方面．（1）复习引入．执教教师原生态的引入方式是用和教材一样的方法，通过复习三色陀螺引入．而改进后的第二、三次课是通过复习圆面积公式的原理．这种安排为帮助学生探究公式设置了有效的铺垫．（2）扇形概念．关于扇形概念，第二次和第三次课都设置了扇形变式图形的辨析，加强学生对扇形概念本质的理解．（3）公式探究．第一次课让学生探究，而公式则由教师通过将弧长公式替代进入经过变形得到．课后研究者询问执教教师为什么这样处理，执教教师回答是因为估计学生无法通过推导得出公式第二、三次课通过复习圆面积公式的原理来引导学生探究扇形面积公式，一部分学生通过探究是可以得出3个公式的．第二次课教师又安排了学生通过特殊角的扇形来探究扇形面积公式，缩小了探究空间，说明这一次课执教教师对研究者的设计意图的理解并不透彻．（4）各环节所占时间．从3次课时间分布的情况来看，3次课有很大差异．特别是公式探究和公式应用所用时间差别较大．第一次课，公式探究用时16′27″，占整节课的41.1%，公式应用17′45″，占整节课的44.3%．第二和第三次课，公式探究时间比第一次课用时长，分别为 22′1″和 25′12″，占比高达 50%和 57%．这是符合现在课堂教学注重学生探究的理念的．相应地，第二、三次课公式应用用时就短了，分别为 15′43″和 13′30″．

4.2 三次课教学效果的对比

从3次课后测试的结果来看，3次课的教学效果有很大差别，第三次课的效果明显优于第一、二次课．

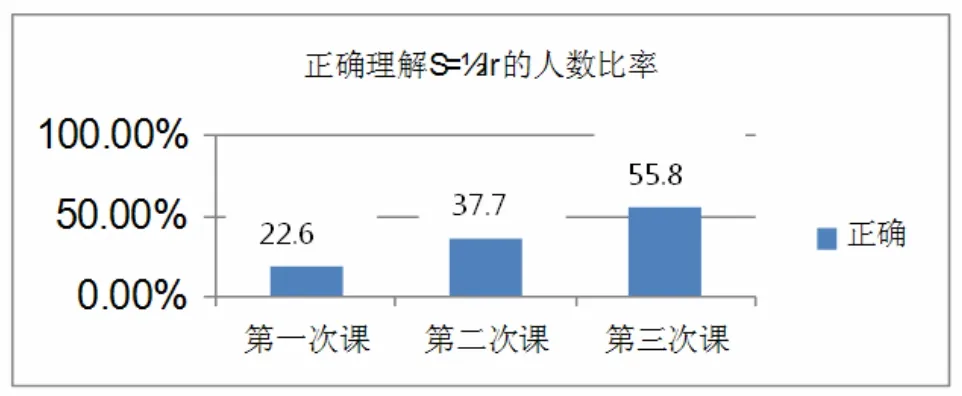
图4 正确理解的人数比率

4.2.2 关于公式的相互推导

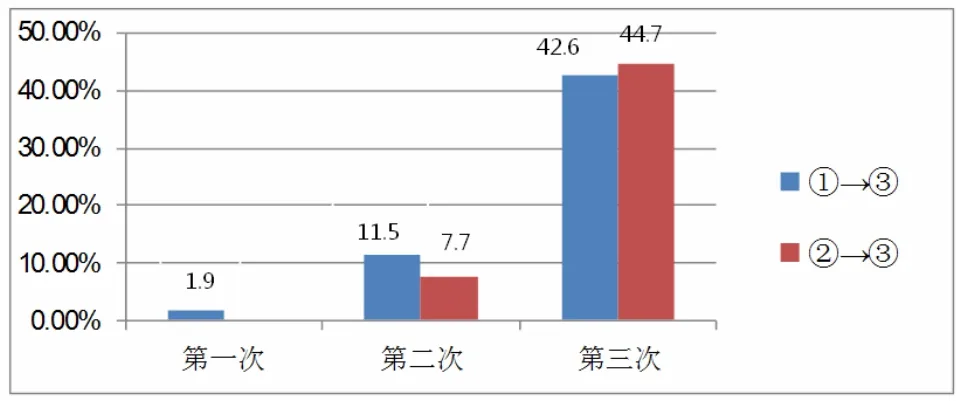
图5 公式相互推导检测结果

4.2.3 关于公式的应用

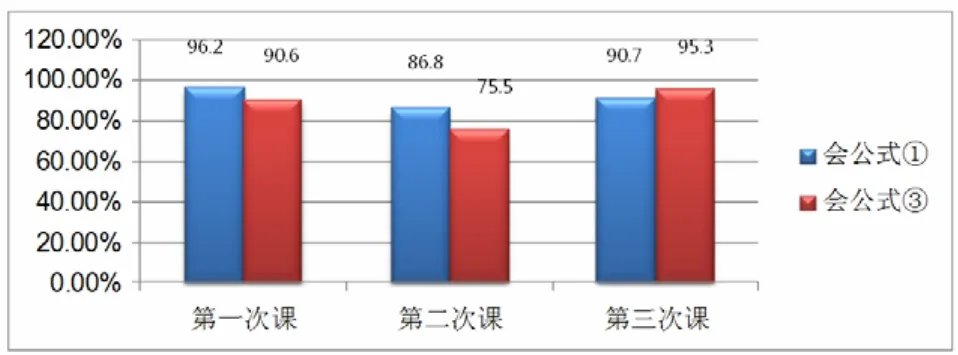
图6 公式的简单应用

关于扇形面积公式的灵活应用，设计的题目是可以让学生选择条件和相应公式的．从正确率来看，3次课分别为81.1%、64.2%和 86%．从灵活性来看，第一次课后学生只会机械代公式计算，第二次课有18.9%的学生会用简便的方法求出结果，第三次课有30.2%的学生会用简便方法．

关于公式的实际应用，从测试结果来看（如图 7），第一次课正确人数占比为26.4%，第二次课为18.9%，第三次课提高到32.6%．从课堂教学情况来看，对于拓展题，第二和第三次课，已经有很多学生可以把扇环想象为梯形，猜出扇环形的面积为学生的思维得到了拓展．

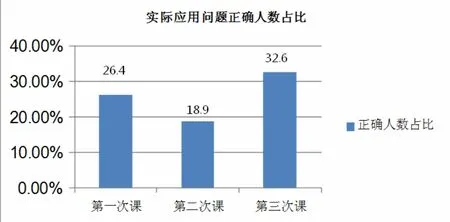
图7 公式的实际应用

从应用测试的结果来看，虽然第三次课探究公式耗时最多，导致公式应用练习相对较少，但是并不影响学生正确掌握公式的应用．

5 指导者的体会

参与这次教研活动的指导者对设计改进的效果有非常深刻的体会．下面是对专家教师和区域层面指导者的访谈片段，时间节点都是在第三次指导会议结束后．

（1）专家教师访谈片段．

访谈人：通过这样一次活动您有哪些体会？

专家教师：通过这样一个活动，这个课无论从对数学本质的探讨和这个上课的顺序以及我们现在比较讲究的课堂效率来说，经过这样一次打磨，那前后肯定不一样的．我们考虑的深度完全没有顾老师来帮我们指导的这么深刻．我们前面还是比较多的关注教材面上的知识，就是比如说前后联系衔接好，类比、局部、部分与整体等，这些都是能够讲到的，包括公式、学生的应用，这些面上的应该是基本上能够完成的，但是没能够像经过这样一轮的探讨之后，提到这样的深度．方方面面的局部和整体，从各个角度各个元素上面去考虑局部与整体，以及互相之间的关联，这些肯定没有顾老师跟我们这样点过了之后这么深，这么多年教下来，基本上没有提到过往往就是像书本一样的，通过扇形的圆心角公式和弧长公式推导出S扇

访谈人：这种代数推导，学生不一定能从几何上去理解．

专家教师：是的．印象非常深刻的，还有一个就是最后我们以前做题从来没有做到梯形舞台这个画成这个曲的这种梯形，曲边三角形倒是也会提到的，因为这个是会想到的，但是扇环形、梯形几乎是想不到．所以说这个深度是达不到的．

而且从上课上下来的这个效果来看，我们以往可能会通过一些具体的题目来发现这通过这样的设计之后，就不需要具体的了，也不需要数字了，通过后面的一节课检查下来，学生通过图形、字母也理解了这两个公式．

访谈人：数形结合比较到位．

专家教师：对的．

（2）区域层面指导者访谈片段．

访谈人：就是这样一次活动，您自身有哪些体会啊？

区域层面指导者：个人的感觉，就是参加这个活动之后，自己也是一个理解教材的过程．最重要我们在做前面那个新旧知识的衔接，本节课的新的知识怎么和学生已有的知识建立本质的联系，这个方面确实想得多了点．然后，这个第三个公式实际上在我们平时的指导当中，肯定是不敢用．就是说，即使你有这个想法也不敢拿出来．现在呢，可以把它拿出来，拿出来之后呢，直接让它建立一个本质的联系．从思想方法上是一个本质的联系，从公式的内部结构来讲也是一个本质的联系．这次教研活动我感觉收获很大．

6 启示与展望

教师专业发展需要指导者，关于教师发展指导者的研究正在进行中．顾泠沅教授认为，教师发展指导者的工作元素有4项：前端分析、任务设计、过程测评和行为改进．前端分析和过程测评，是教学必须以学生的发展为本的两个重要方面，任务设计和行为改进，是教师工作专业化的两项基本实践．关键在于怎样基于学情以及课程改革要求设计教学任务，怎样通过过程测评不断改进教学过程．中国的教研指导水平很高，但这两项目前尚是瓶颈．

此次教学研究活动，是教师发展指导者根据学情和对学科知识分析的基础上进行设计改进的一个案例．从教学效果来看，这次设计是卓有成效的．教师发展指导者和教师应该具有创新精神，不仅要从行为上改进教学，更要注重设计思路的改进．

关于教师发展指导者的工作，美方和日方也在积极研究中，美方的Lynn Paine教授主要研究教师发展指导者的知识结构问题，日方重点放在课例（Lesson Study）的研究上．研究者即将进行更多的后续研究，如教师发展指导者如何进行课前指导，对新老教师指导的差异有哪些，以及教师发展指导者自身的专业发展等，并即将推出一个教师发展指导者工作的模式．

[1]王洁，顾泠沅．行动教育——教师在职学习的范式革新[M]．上海：华东师范大学出版社，2007．

[2]顾泠沅．教师发展指导者工作的研究[R]．上海：中、美、日三国教师发展指导者预研究研讨会，2011．

[3]李士锜，杨玉东．教学发展进程中的进化与继承——对两节录像课的比较研究[J]．数学教育学报，2003，12（3）：5-9．

[4]James W Stigler, Shin-ying Lee, Harold W Stevenson. Mathematics Classrooms in Japan, Taiwan, and the United States[J]. Child Development, Special Issue on Schools and Development, 1987, 58(5): 1 272-1 285.

[5]顾非石，俞宏毓，顾泠沅．探究学习的设计与改进——关于一个课例的述评[J]．课程教材教法，2012，（5）：116-119．

[6]黄兴丰，庞雅丽，李士锜．数学课堂教师教学行为的继承和发展——3节录像课的比较研究[J]．数学教育学报，2009，18（6）：54-57．

[7]斯海霞，叶立军．新老教师数学抽象概括教学差异的比较研究[J]．数学教育学报，2010，19（6）：53-55．