四点接触球轴承摩擦力矩特性分析

陈龙，史朋飞，李正国，邱明，夏新涛

(河南科技大学 机电工程学院，河南 洛阳 471003)

1 概述

与深沟球轴承相比，四点接触球轴承承载能力更高；与角接触球轴承相比，四点接触球轴承可承受双向轴向载荷；与成对双联角接触球轴承相比，四点接触球轴承的极限转速高并且轴向窜动小[1-3]。由于四点接触球轴承的一系列优点，故得到了广泛的应用。大型转盘轴承多采用四点接触结构，依据承载能力高低要求，目前使用的四点接触转盘轴承有单排球结构、双排同径球结构和双排异径球结构等[4-7]。受装配因素影响，小型四点接触球轴承内圈或外圈需采用半圈结构，如QJF000型双半外圈四点接触球轴承(图1a)和QJ000型双半内圈四点接触球轴承(图1b)[8-9]；内、外圈为整体结构的四点接触转盘轴承(图1c)则采用专门的装球孔进行装配[4]。小型四点接触球轴承套圈材料一般采用GCr15，大型四点接触球转盘轴承套圈材料则采用50Mn或42CrMo[10]。小型四点接触球轴承沟道加工时大部分采用修整砂轮切入磨削，大型四点接触球转盘轴承套圈采用切入磨削或数控硬车[11]。轴承沟道的加工误差对于钢球与沟道的接触位置有着显著影响，实际生产中大多采用刮色法检测接触位置，这种检测方法不能进行定量检测，也难以确定其实际接触角[12-15]。实际接触点位置的改变直接影响接触角的大小，进而影响到四点接触球轴承的游隙值[10, 15-19]及其内部的载荷分布状态[5]。

图1 四点接触球轴承的结构类型

摩擦力矩的大小决定了轴承的功耗和温升，是轴承的一个重要性能参数。轴承摩擦力矩受众多因素，如结构、设计、加工、摩擦、润滑及使用条件等的影响[20-22]。

采用不同模型计算同型号轴承的摩擦力矩值，对比分析模型的差异，找出计算值差异的原因，有助于确定影响摩擦力矩的关键几何因素。

2 摩擦力矩的理论计算模型

2.1 SKF的修正计算模型

对于四点接触球轴承，SKF公司提出的修正摩擦力矩计算模型为[23]

M=φishφrsMrr+Ms1+Mseal+Mdrag，

(1)

(2)

式中：φish为切入发热减少系数；φrs为贫油回填减少系数；Mrr为滚动摩擦力矩；Msl为滑动摩擦力矩；Mseal为密封件摩擦力矩；Mdrag为由于拖拽损失、涡流和飞溅等导致的摩擦力矩；Dpw为球组节圆直径；n为轴转速；ν为润滑油动力黏度。此计算模型未考虑内部几何参数对摩擦力矩的影响。

由于试验选用了L61润滑脂，故直接采用脂润滑条件下的简化模型，

(3)

Mrr=Grr(ν1n)0.6，

(4)

(5)

Msl=Gslμsl，

(6)

(7)

式中：D为轴承外径；d为轴承内径；ν1为润滑剂在工作温度时的运动黏度；Fr为径向载荷；Fa为轴向载荷；μsl为滑动摩擦因数。

(5)式和(7)式中的Fr与Fa为外载荷。由(1)～(7)式可知，外形尺寸相同的四点接触球轴承的摩擦力矩应一致，但实测数据却相差很大。

2.2 考虑内部几何结构参数的计算模型

产生摩擦力矩的根本因素在于内、外圈与钢球之间的相互运动。由于此类轴承一般装用较高精度的钢球，即钢球精度比沟道精度要高，故下面研究沟道精度对于轴承摩擦力矩的影响。

Florin T提出了考虑轴承内部几何结构参数的四点接触球轴承摩擦力矩计算模型[24]。与SKF计算模型相比，该计算模型中考虑了材料弹性滞后造成的摩擦因素，以及钢球与保持架、保持架与套圈之间的摩擦。

总的摩擦力矩为

M=Mrr+Msl+Mhys+Mcol+Mlub，

(8)

式中：Mhys为钢球受载产生弹性滞后产生的摩擦力矩；Mcol为保持架产生的摩擦力矩，包含钢球与保持架以及保持架与套圈之间的摩擦；Mlub为润滑剂造成的摩擦力矩。

(9)

(10)

材料弹性滞后造成的摩擦力矩为

(11)

式中：Dw为钢球直径；Z为钢球个数；ωi为内圈转动的角速度；ri为内圈沟曲率半径；re为外圈沟曲率半径；βi为钢球与外圈接触的材料特性与几何特征系数；βe为钢球与外圈接触的材料特性与几何特征系数；μ为摩擦因数；α为接触角；σi为第i个钢球受载后发生Hertz接触变形的最大值。

保持架产生的摩擦力矩Mcol为

Mcol=Mcolb+Mcole+Mcoli。

(12)

保持架产生的摩擦力矩包括钢球与保持架的摩擦力矩Mcolb、保持架与外圈之间的摩擦力矩Mcole以及保持架与内圈之间的摩擦力矩Mcoli，即

(13)

式中：Decag为保持架外径；Dicag为保持架内径；ε为保持架的偏心率；Rca为保持架兜孔半径。

由于拖拽损失、涡流和飞溅等导致的摩擦力矩Mdrag为

(14)

式中：f0为系数；v1为润滑剂与钢球相对速度。

2.3 理论计算模型的计算结果对比

以四点接触球轴承JY204为例进行计算，该轴承套圈的几何结构参数见表1。利用SKF修正模型计算其摩擦力矩为11. 6 mN·m；利用Florin T模型计算结果为52. 3 mN·m。

表1 轴承套圈结构参数

对比两种计算模型，SKF计算模型中纳入计算的轴承几何尺寸参数只包括轴承的内、外径与球组节圆直径，而Florin T的计算模型中，除考虑这些参数之外，还考虑了钢球直径，钢球个数，接触角，套圈的沟曲率，保持架的内径、外径、兜孔半径及其偏心率等参数。针对具体型号的摩擦力矩计算上，显然Florin T的计算模型考虑得更为完善，后续的试验数据也表明该模型的计算值更接近实测值。

Florin T的计算模型中，其他几何参数的误差对于计算值的影响较小，影响最为突出的因素为接触角α。本计算中几何参数的代入值均为设计值，没有考虑加工误差的影响。而四点接触球轴承实际接触角的影响因素很多，包括轴承的轴向游隙Ga、几何尺寸参数(内沟道或外沟道的接触点直径D5或d5、内外沟道的沟底直径D1或d1、内外沟道的沟曲率半径re1与re2或ri1与ri2)、沟道形位公差(包括套圈接触点位置的圆度Cir、对称沟道中心与端面平行度Se与Si、外圈或内圈沟道接触点与外圈或内圈表面间的厚度变动量Ke与Ki、两对称沟道相对于基准面厚度变动量Ker，沟道的轮廓度ΔCur)等，如图2所示。这意味着实测值与考虑内部几何结构参数的理论计算模型值仍将有较大差异。

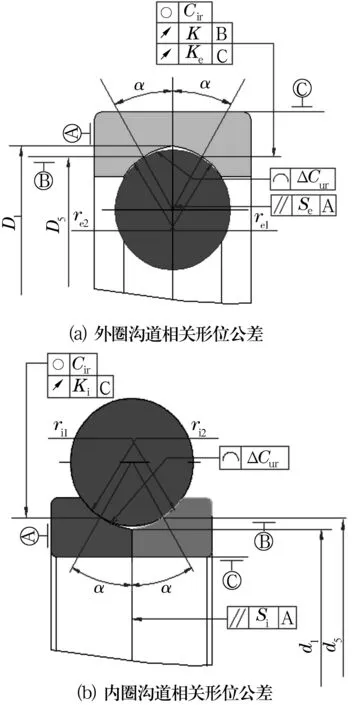
图2 影响四点接触球轴承实际接触角的沟道尺寸与公差

在沟道的几何参数中，沟道的接触点直径误差直接影响游隙值的大小，对接触角产生直接影响；沟道曲率半径的误差以及同一套圈的两沟道之间曲率的一致性也将影响游隙值并最终影响接触角。因而实际生产中应严格控制内沟道或外沟道的接触点直径D5或d5，以保证合套率、游隙值以及正确的接触角。严格控制接触点直径还能消除部分由于沟曲率误差造成的接触角变化。

在形位公差参数中，Se(Si)，Ker或ΔCur可造成单一截面上实际接触角与理论接触角的差异；Cir或Ker可造成圆周面上的实际接触角变化。

3 游隙对实际接触角的影响

3.1 原始游隙的影响

轴承的游隙包括装配游隙、安装游隙以及工作游隙，轴承从装配完成到使用过程中，若游隙发生变化，则其接触角也将产生变化。由于轴承内部游隙的存在而造成的接触角变化如图3所示，图3a为径向游隙造成的实际接触角变化，图3b为轴向游隙造成的实际接触角变化。假定外圈沟曲率系数为fe，内圈沟曲率系数为fi，轴承初始外圈上沟道曲率中心为Ceu，外圈下沟道曲率中心为Ced；内圈上沟道曲率中心为Ciu，内圈下沟道曲率中心为Cid；钢球初始中心为O。则内圈上沟道与外圈下沟道沟心距为

图3 四点接触球轴承游隙对接触角的影响

A=(fi+fe-1)Dw，

(15)

设计接触角α0为

(16)

径向游隙为Gr，设计接触角为α0，假设外圈固定，内圈移动，则沿径向移动距离为Gr/4，则接触角由α0变化为αr；轴向游隙为Ga，设计接触角为α0，假设外圈固定，内圈移动，则沿轴向移动距离为Ga/4，则接触角由α0变化为αn。

(17)

3.2 曲率变化的影响

目前四点接触球轴承沟道终加工除部分采用数控硬车外，大量采用切入磨加工。采用切入磨法加工沟道时，沟道形状靠砂轮修整出来的形状保证，砂轮修整精度以及磨削过程中的砂轮磨耗对于沟道形状有直接影响。

沟道曲率变化对实际接触角的影响如图4所示。图4a为沟曲率增加使实际游隙增大，进而导致接触角增大；图4b为沟曲率减小使实际游隙减小，进而导致接触角减小；图4c与图4d为沟道曲率不一致(偏沟)导致的接触角变化。对于带预紧的负游隙四点接触球轴承，沟道曲率不一致会严重阻滞钢球回转，增加摩擦力矩。但对于游隙为正的四点接触球轴承，其影响形式仍为游隙变化造成的接触角变化。

图4 沟曲率对接触角的影响

为了更清晰地说明问题，图4选取沟底径作为沟曲率变化的基准位置，但实际生产中控制的是沟道接触点尺寸，保证接触点位置可适当消除由于沟曲率误差导致的游隙与接触角的变化。

4 沟道形状对实际接触角的影响

在加工精度的影响因素中，除几何尺寸变化造成游隙变化进而影响接触角外，形位公差造成的实际接触角变化的波动性更为显著，进而导致摩擦力矩的波动。由于砂轮形状不恰当时形成的沟道形状示意图如图5所示，图5a为单一截面示意图。由图可知，单一截面上，Se(Si)，Ker和ΔCur的偏差都将影响到实际接触角的大小，整个回转面上，Cir或Ker导致轴承转动时的实际接触角变化。

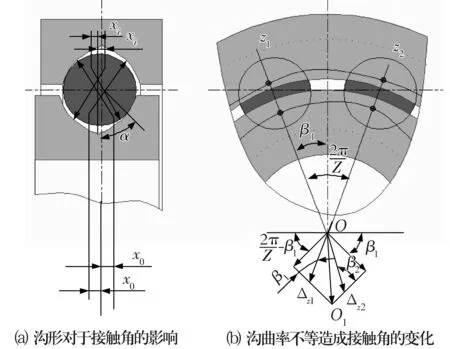
图5 形位公差对四点接触球轴承接触角的影响

当要求轴向游隙时，对(17)式计算其全微分(为了表达更清晰，全微分时将内、外沟道沟曲率系数以沟道半径与钢球直径的比值的形式表示)，则有

(18)

则在单一截面上由形位公差造成各尺寸公差反映到接触角的变化上可以表示为

(19)

图5b为钢球从OZ1位置转动到OZ2位置的过程中，由沟道的形位公差造成的钢球位置、接触角以及摩擦力矩的变化。由沟形变化产生的附加摩擦力矩为

(20)

式中：Δz1和Δz2为Z1与Z2方向上由沟形变化导致的位置变化量。

5 试验

5.1 试验方案

为研究沟道形状对于摩擦力矩的影响关系，选取10套JY204四点接触球轴承进行试验。首先采用东京精密1600D轮廓仪测量轴承内、外圈的接触角。指定轮廓仪的原因在于其他类型轮廓仪尚无法测量套圈的接触角。需要指出的是：采用1600D测量零件实际接触角的过程，是轮廓仪依据测量结果绘制出沟道实际轮廓后，利用仪器后台程序将钢球直径的理论值与绘制出的沟道实际轮廓相切，从而得到零件的实际接触角。装配时钢球的实际直径值与理论值之间存在尺寸误差，故该测量方法存在一定的原理误差。但由于钢球精度相对于沟道精度要高，所以该误差影响可以忽略。

因为四点接触球轴承装配后钢球与内、外圈沟道同时接触，所以文献[7]提出了桃形沟道接触点测量方法，采用测长仪测量并换算成实际接触角。但文献[7]介绍的是特大型四点接触球转盘轴承的实际接触角测量方法，而本试验轴承尺寸较小，故测量精度很低。

使用德国Mahr 828PC测长仪测量，其分辨率为0.01 μm，精度为0.15+L/2 000 μm。测长仪的原测头为尖顶，为了满足试验要求，在测长仪端部焊接试验轴承装用的钢球，钢球直径3.968 8 mm，分规值-2 μm。使用测长仪测量接触点位置到基准位置的距离并换算成实际接触角。

最后将试验套圈合套测试摩擦力矩，测试时不加载，水平放置，内圈固定，外圈旋转，转速为100 r/min。

5.2 结果分析

测试结果见表2。测量所得摩擦力矩值与两种计算模型的计算结果差异都很大(SKF修正模型计算结果为11. 6 mN·m；接触模型计算结果为52. 3 mN·m)，实测值远远大于计算模型的计算值。

对比轮廓仪与测长仪的测试结果，测长仪测量并换算的内、外圈接触角数值处于轮廓仪测量的上、下沟道接触角中间，这是由于空间限制，测长仪的测头难以保证与上、下沟道同时接触；另外，测长仪采用实际钢球，钢球尺寸误差也影响到测试结果，但测试结果的分布状态能说明测量的可靠性。

采用轮廓仪测试时可判断同一内圈的曲率状态，采用测长仪加装配钢球测量时，无法分别测量出上、下沟道的接触角，而是上、下沟道接触角的综合反应。序号为1，2与5的测长仪换算接触角接近，其摩擦力矩值也较为接近。因而可判断出实际接触角对于实际摩擦力矩的影响非常显著。

6 结束语

目前较为先进的2种四点接触球轴承摩擦力矩计算模型中，摩擦力矩计算值差异均较为突出，2种计算模型计算值的差异在于有无考虑轴承内部几何结构参数。本例设计了专门试验测试四点接触球轴承摩擦力矩以研究内部结构参数对于摩擦力矩的影响。

实测的摩擦力矩值远大于理论模型的计算值，分析认为沟道加工精度对于摩擦力矩的影响也非常突出。对比实际接触角接近的试验样本，发现轴承摩擦力矩也较为接近。