基于声发射检测技术的转炉耳轴轴承故障诊断

路俏俏, 黎敏, 阳建宏, 徐金梧, 胡军

(1.北京科技大学 机械工程学院，北京 100083；2.鞍钢股份有限公司，辽宁 鞍山 114021)

转炉是炼钢生产中的重点设备，耳轴轴承是转炉倾动机构的重要部分，支撑着炉体、液态金属、钢渣、托圈及其附件的全部质量和悬挂减速机的质量，耳轴轴承的工作状态对保障生产的稳定运行具有重要影响，一旦设备出现事故，将会严重影响生产，导致重大经济损失。所以，对转炉耳轴轴承的监测具有重大意义。耳轴轴承转速在1 r/min左右，通常在-95°～190°范围内进行非连续性旋转，大部分时间处于静止状态，只有在工序需要时进行时断时续的旋转[1]。针对耳轴轴承负载重、转速低、非整周期旋转且旋转不连续等工作特点，传统的振动检测方法难以进行有效的诊断分析[2-3]。因此，需要针对低速重载设备，研究新的检测技术和模式识别方法。

声发射(Acoustic Emission, AE)是材料受外力作用产生变形、断裂后，以瞬态弹性波形式释放应变能的现象。对滚动轴承而言，在无故障的状态下，轴承各组成部分接触面间的相对运动、碰摩所产生的接触应力会诱发声发射信号。此外，由于润滑不良造成的表面粗糙，以及由于温度过高、载荷过大等原因而产生的磨损、裂纹、压痕等故障也会使得滚动轴承在运转过程中产生声发射信号[4]。

在滚动轴承故障的早期，由于故障能量比较微弱，不能激起设备表面的振动，利用振动分析方法难以提取设备的早期故障。而声发射信号来自于缺陷本身，只要有故障存在且处于不断扩展状态中，都会以应力波的方式释放出能量，并能被高灵敏度的声发射传感器所接收[5-6]。因此，声发射检测技术能够有效发现设备的早期故障，从而可以利用声发射信号对轴承的状态进行监测与诊断分析。

1 轴承声发射信号的模式识别方法

采集不同状态下耳轴轴承的声发射信号，首先计算声发射特征值，然后利用主成分分析方法进行特征提取，再输入到最小二乘支持向量机中进行故障识别，最终实现转炉耳轴轴承的故障识别。

1.1 声发射的特征值计算

为了客观描述一个声发射事件，通常需要计算多个特征值来刻画声发射的物理过程。常用的特征值主要包括：幅值、能量、上升时间、持续时间、振铃计数、均方根值、平均电平等。特征值的计算示意如图1所示。

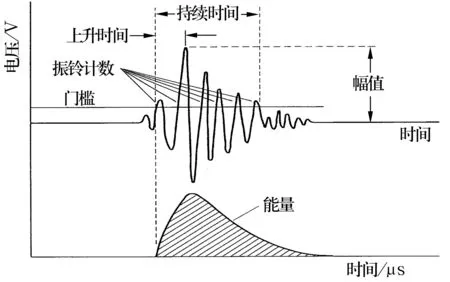
图1 声发射特征值的计算示意

从图1可以看出，幅值实质上是一个声发射信号的最大值；能量是信号检波包络线下的面积，是整个声发射信号强弱的体现；上升时间是信号第一次越过门槛至最大振幅所经历的时间；而持续时间则是信号第一次越过门槛值，到幅值最终降至门槛所经历的时间，主要体现信号的衰减特征；振铃计数表示越过门槛值的振荡次数，可以粗略反映信号的强度和频度；均方根值也称为有效值，以另一种方式反映了信号的能量大小；平均电平即为信号的平均值。通过上述分析发现，可以通过计算不同的特征值来全面反映一个声发射事件的本质信息。

1.2 基于主成分分析的特征提取

由于各个声发射特征值之间存在一定程度的相关性，且高维数据的输入会增加分类器识别算法的复杂度，降低识别正确率，算法时间也将大幅延长。因此，需要对多维数据进行特征提取。主成分分析法是一种多变量分析方法，主要目的是对多变量数据进行最佳综合简化，即在保证数据信息丢失最小的原则下，对高维数据进行降维处理，把原来存在内在关联的变量变为不相关的若干新变量，而这些新的变量将携带尽可能多的原始数据信息，从而实现数据的特征提取。

假设X是一个n×m的数据矩阵，其中的每一列对应一个声发射特征值，每一行对应一个声发射样本。首先，将X进行标准化处理为E，即按列分别减去均值除以标准差；其次，计算标准化数据E矩阵的协方差矩阵ETE；再求取协方差矩阵ETE的特征值λ1≥λ2≥…≥λm和对应的特征向量P1,P2,…,Pm；然后计算特征能量

(1)

如果当前h个特征值的和超过全部m个特征值总和的80%，则认为所对应的前h个特征向量保留了原信号中的绝大部分信息，则计算得到主成分为

tj=E·Pj,j=1,2,…,h。

(2)

将这h个主成分tj构成新的特征值矩阵Xn×h，并作为分类特征输入到分类器中进行模式识别。

1.3 基于最小二乘支持向量机的特征识别

支持向量机(Support Vector Machine，SVM)是目前有效解决小样本、非线性和高维数据问题的新型机器学习方法。假设给定线性可分的样本集(Xi,yi)，i=1,2,...,n，n表示样本的个数，yi∈{-1,1}。以两类分类问题来说明SVM的核心思想。首先要获得一个最优分类面，不仅能将两类样本正确区分，而且要使分类间隔最大，即需满足

yi[(w·Xi)+b]≥1，

(3)

支持向量机的训练速度慢和难以大规模运算是制约其发展和推广的重要原因。作为经典支持向量机方法的发展和改进，最小二乘支持向量机(Least Squares SVM，LS-SVM)采用等式约束替代不等式约束，求解过程变成解一组等式方程，避免了求解耗时的二次规划问题，求解速度大大加快[7]。

LS-SVM以最小二乘线性系统为损失函数，代替SVM采用的二次规划方法。通过求解线性方程组保证‖w‖2最小化，获得最优分类面，即需满足

(4)

式中：φ(Xi)为非线性变换函数；允许错分的松弛变量ηi∈Rn；γ为可调正则化参数，控制对超出误差样本的惩罚。为求解上述优化问题，把约束优化问题变成无约束优化问题，定义Lagrange函数

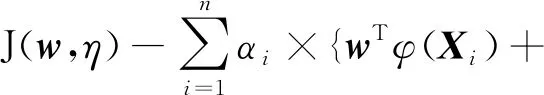
b+ηi-yi}。

(5)

分别求L对αi，w，b，ηi的偏导数，联立求解方程后，可得到最优分类函数

(6)

式中：K(X,Xi)为核函数，常用的核函数有线性核、高斯核、径向基核等，核函数的选择与分类效果密切相关。

(6)式实质上可以看作是一个分类模型。首先利用大量样本进行训练，目的是要获得模型中的各个系数。当新来一组待识别的样本集时，进行相应的特征值计算和PCA特征提取后，可以直接输入分类模型中，实现声发射信号的模式识别。具体流程如图2所示。

图2 声发射信号的模式识别流程

2 试验验证

利用美国PAC公司的SAMOS声发射仪对某钢厂容量均为260 t的A，B两个转炉从动侧的耳轴轴承进行声发射信号采集。轴承以1 r/min左右的速度做非整周期、非匀速旋转。将声发射传感器分别安装在轴承座承载区的45°方向，如图3所示。采样频率500 kHz，连续采集30 s内空炉摇炉状态下声发射信号。利用A,B炉各600个声发射样本进行训练，各300个声发射样本用于测试。参与训练的样本的各个特征值曲线如图4、图5所示。

图3 转炉耳轴轴承测点布局图

图4 A炉训练样本的特征值曲线

图5 B炉训练样本的特征值曲线

从图中可以看出，B炉的特征值普遍高于A炉的特征值，可以初步判断A炉的状态优于B炉的状态。但当新来一组样本时，该如何判断其状态的好坏是进行故障诊断的关键。因此，需要研究分类识别的算法来进行故障诊断。首先，利用主成分分析方法对图中的9个特征值进行特征提取，当取h=3时，可满足(1)式的要求，将9个特征值融合为3个综合参量，这3个综合参量保留了原信号中80%以上的信息，可将它们输入到分类器中进行模式识别。

为了评价分类识别的效果，需要定义一个评价指标以反映分类器对数据集分类识别的平均性能。用总体正确率表示为

(7)

式中：TA为A类样本中被准确识别为A类的样本个数；FA为A类样本中被误识别为B类的样本个数；TB和FB以此类推。

为验证本文方法的有效性，设计了3个试验，见表1。

表1 转炉耳轴轴承分类识别结果

比较试验1与试验2的结果可以看出：运用LS-SVM新的模式识别方法，核函数为线性核时，可以将传统SVM方法的总体正确率从71.39%提高到80%，且运行时间缩短为原来的10%，当使用高斯核函数时，也有类似的结论。

比较试验3和试验2的结果可以看出：利用PCA方法进行特征提取后，再输入到LS-SVM分类器中进行模式识别，总体正确率进一步提高到97.8%。更重要的是，在试验3中可以看出：通过PCA降维处理后的数据，使用线性核函数与使用高斯核函数的总体正确率非常接近。而在试验1和试验2中，使用不同的核函数的总体正确率却有近10%的差距，说明使用PCA进行特征提取后，不必再使用复杂的高斯核函数，使用线性核函数就可同样得到较高的总体正确率，这样不仅降低了算法的复杂度，也缩短了算法的运行时间。

经过现场油液分析的验证，A炉耳轴轴承处于正常状态，而B炉耳轴轴承存在磨损现象。为进一步说明方法的有效性，以线性核函数为例，给出了利用试验3的方法对两类样本分类的结果，见表2。

表2 试验3的分类结果

从表2可以看出，对正常状态的样本分类正确率为99%，对磨损状态的样本分类正确率为96.6%，说明所设计的分类器能够较准确地识别出两种不同的轴承状态。

3 结论

(1)针对转炉耳轴轴承低速、重载、非整周期、间歇旋转的工作特点，采用声发射技术对耳轴轴承进行状态监测是一种新监测技术的有益尝试，可以为具有类似工作特点的设备提供参考。

(2)将PCA特征提取方法和LS-SVM分类方法相结合，对正常和磨损状态下的转炉耳轴轴承进行故障识别，在使用线性核函数数时，总体正确率可达到97.8%，且算法复杂度低，运算速度快，可为转炉耳轴轴承的在线监测与故障诊断提供有力支持。