模糊合作对策区间Shapley值法的改进及应用

王晓艳，殷 辉，2

1.合肥学院 管理系，合肥 230601

2.浙江大学 管理学院，杭州 310058

模糊合作对策区间Shapley值法的改进及应用

王晓艳1，殷 辉1，2

1.合肥学院 管理系，合肥 230601

2.浙江大学 管理学院，杭州 310058

1 引言

合作对策发展至今一般分为两类[1]：经典合作对策和模糊合作对策。经典合作对策基于两个假设：局中人完全参与到一个特定的联盟之中；局中人在合作之前完全清楚地知道不同的合作策略所产生的收益，以及自身参与特定联盟的所得分配。现实中，由于合作过程的复杂性，决策环境的不确定性，对问题认识的模糊性，所得信息的不完全性等因素，使得模糊环境下，n人对策理论研究已成为当前对策论研究领域的一个热点问题。模糊合作对策的研究主要体现在两个方面[2]：（1）对具有模糊联盟n人对策的研究；（2）对具有模糊联盟值n人对策的研究。Aubin[3]在 1974年首次提出了模糊合作对策的概念，该类对策的联盟是模糊集，收益是清晰的实数，并对模糊合作对策的解展开了深入研究[4]。Sakawa和Nishizaki[5]于1992年提出了一类新的模糊合作对策，该类对策的联盟是清晰集，但收益却是模糊数。Mares[6]于1995年指出具有模糊支付函数的合作对策也是模糊合作对策的一种形式。

无论何种合作对策，其核心问题都是关于合作收益分配的探讨。Shapley值法[7]在解决经典合作对策中合作收益的分配上得到了广泛的应用。Butnariu[8]研究了具有模糊联盟n人对策的Shapley值，但该Shapley值与经典的Shapley值相比，既不单调非减又不连续。针对这一问题，Τsurumi等[9]在Butnariu的基础上构造了一个在Choquet积分上的模糊Shapley值，使其单调非减且连续。Branzei等[10]从另一角度对具有模糊联盟合作对策的Shapley值的概念作了定义，但对于局中人在一定参与水平下的支付分配问题，他们没有提供有效的分配方法。Butnariu等[11]在文献[8]的基础上，研究了一类更一般化具有模糊联盟n人对策的Shapley值。Li等[12]给出了具有模糊联盟n人对策Shapley值的一种简单表示形式。

另一方面，考虑到合作人的模糊偏好会导致联盟收益的不确定性，Mares[13]对模糊收益问题进行了探索性研究，求得了Shapley值的模糊隶属函数，但没有给出具体的分配方案。Borkotokey[14]从模糊联盟的角度，研究了具有模糊联盟和模糊支付的合作对策。具有区间支付的合作对策是一种特殊形式的模糊合作对策。国内不少学者对区间Shapley值法开展了研究。陈雯等[15]利用模糊数学的理论与方法，提出了满足有效性、对称性和可加性的模糊Shapley值，但是此模糊Shapley值不一定存在。于晓辉等[16]分析了合作对策中支付函数是区间数的情形，提出具有区间支付的合作对策的Shapley值，但该方法不具一般性。谭春桥[17]通过建立公理化体系，研究了一般意义下具有区间支付的合作对策的Shapley值。

通过分析不难发现，上述文献中提出的区间Shapley值法能够体现合作者在合作中的总体贡献以及重要性，为不确定性合作收益的分配提供了较好的参考，但该方法对产生贡献的因素没有细分，对不同因素也没有给予不同的权重，只是对合作者贡献的模糊反映[18]。因此，有必要对区间Shapley值法进行改进。鉴于此，本文在已有研究的基础上，分析清晰联盟在预期收益不确定的情况下，如何结合联盟自身固有的特点，建立联盟收益分配评价指标体系，引入收益分配的综合修正因子，对模糊合作对策的区间Shapley值法进行改进，并列举实例用改进后的模型对收益进行分配。

2 具有区间支付的模糊合作对策和区间Shapley值法概述

二元组(N，)称为局中人集合N={1，2，…，n}上的模糊合作对策，其中是定义在N的幂集P(N)上，取值在区间数集合上的模糊支付函数，即)→且=0。区间支付函数=[ν-(S)，ν+(S)]表示联盟S∈P(N)中各个局中人通过合作所能得到的最大收益区间，ν-(S)是联盟S中的各个局中人共同合作可能获得收益的最小值，ν+(S)是S中各个局中人共同努力可能获得收益的最大值。称具有区间值支付的模糊合作对策为具有区间支付的模糊合作对策，并把区间模糊合作对策集合记做GI(N)[16]。在此，假设∀S⊆N，。

定义1对于具有区间支付的合作对策GI(N)，若∀T∈P(N)，S∈P(N)都满足：=，则称S为GI(N)上的承载（carrier）。

可以证明承载之外的任一局中人对任何联盟都没有贡献。

定义2设N={1,2,…，n}，对于任意的(N)，具有区间联盟值n人对策ν的Shapley值是满足下述公理体系的一个向量函数→，

公理1（区间有效性）对于的任何承载S，有

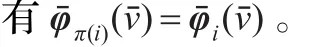
命题1下试所定义的向量函数→，是对策ν的Shapley值向量。

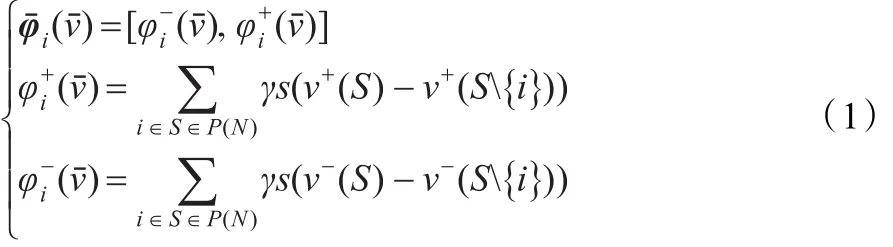
证明过程见文献[17]。

定义3对于对策(N，，向量函数且若被称做具有区间支付的合作对策(N，ν)上的一个分配，则需要满足以下条件：

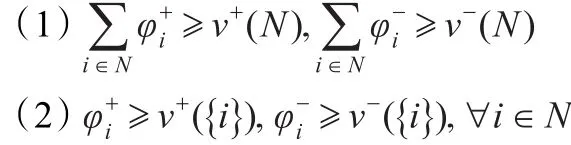
可以证明[17]区间Shapley值是经典合作对策的Shapley值的一个自然模糊延拓，而且支付函数由区间数来表示也更加贴近现实。

3 模糊合作对策的区间Shapley值法的改进

模糊合作对策的收益分配是个复杂问题，受很多因素的影响，如合作方的风险承担、合作努力、市场竞争、创新贡献和资源投入等。这些因素都应该参与利益分配，而且不同因素有着不同的重要性[18]。因此，有必要对区间Shapley值法进行改进。本文运用命题1中的区间Shapley值法对模糊合作对策的收益进行初步分配，将该收益分配作为最终收益分配的评价因素之一。然后用AHP-GEM[19]法（层次分析法和群组决策特征根法）确定收益分配指标的权重。在此基础上，用模糊综合评价法计算各合作方利益分配的综合影响因子。引入综合修正因子，对区间Shapley值法进行改进，建立利益分配的改进模型。

3.1 收益分配评价指标及其权重的确定

用AHP-GEM法确定模糊合作对策收益分配评价指标及其权重的步骤如下：

（1）选取评价指标并建立递阶层次结构。根据各联盟自身的特点，选取评价因素，构建收益分配指标体系的递阶层次结构模型，包括目标层、准则层和指标层。

（2）构造专家评分矩阵。按照构建的递阶层次结构，准则层构建一级评判矩阵，指标层按照准则层构建二级评判矩阵。评判矩阵的构建方法为：由专家群组G中的m个专家直接对n个被评指标进行打分，评分就组成m×n阶矩阵，为：X=[xαβ]m×n其中，xαβ∈[α，β](α=1，2，…，m;β= 1，2，…，n)为第α个专家Sα对第β个被评价指标的评分值，xαβ的值越大目标指标越优。

（3）评价相对权重的计算。基于计算出单一准则层下指标的权重，归一化即得评价指标的相对权重。具体算法为：将评分矩阵X转置自乘记为F，即F=XΤX，F的最大特征根对应的特征向量就是最优决策X*。是基于理想专家模型的构建为基础的，若想得到被评价目标的排序，就要认知理想专家定义，并建立理想专家模型。求出的理想专家的评判分，即为多个被评价目标的排序。

理想专家定义：具有评分向量与群体中各专家评分向量夹角之和最小的专家称为该群体的理想（最优）专家。

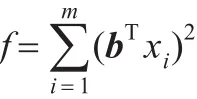
理想专家模型求解：对于理想专家模型的求解有很多种方法，常见的有两种。一是设定精度要求ε，并在此条件下采用数值代数中的幂法进行矩阵F的迭代运算，可以求出X*；二是用软件求解矩阵F的最大正特征根ρmax，X*就为ρmax对应F的正特征向量。

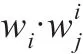
显然，将AHP与GEM相结合，既可以保留AHP中递阶层次结构这一科学分析问题的过程，又能绕开Saaty矩阵构建的不一致性问题，使得多指标决策更具有科学性和准确性。

3.2 收益分配综合影响因子的计算

在确定评价指标权重的基础上，用模糊综合评价法计算各合作方收益分配的综合影响因子。步骤如下：

（1）构造评语集。评语集划分为五个等级，即：V= (V1，V2，V3，V4，V5)=（高，较高，中，较低，低）=（0.9，0.7，0.5，0.3.0.1）。

（2）构造隶属度子集Ri。请有关专家参照评语集V对联盟中各合作方的评价指标进行评价，得模糊子集Ri= (ri1，…，rij，…，ri5)。Ri指评价指标中第i个指标对应的评语集的隶属度，即rij=第i个指标选择Vj等级的人数/参与评价的总人数，其中j=1，2，…，5。经过模糊变换，得到模糊评判矩阵R。

（3）最后把模糊评判矩阵R与评价指标的权重向量集W进行模糊运算，得到模糊综合评判结果集B，B=W⊙R，采用模糊分布法进行指标归一化处理，得B′=(b1，b2，b3，b4，b5)。于是，联盟利益分配的综合影响因子Pi=B′VΤ，再经归一化处理后得。

3.3 考虑综合修正因子的区间Shapley值法

在没有考虑风险承担、合作努力、市场竞争、创新贡献和资源投入等因素的情况下，在n人联盟中，区间Shapley值法假定各合作方上述因素所创造的收益均相等，即为1/n。由上述计算可知，合作方i的综合影响因子为Pi'，其

设由n个合作方组成联盟总收益区间为= [ν-(S)，ν+(S)]，则合作方i实际分配改进量为=DPi×，可正可负。合作方i实际获得的收益分配区间为：

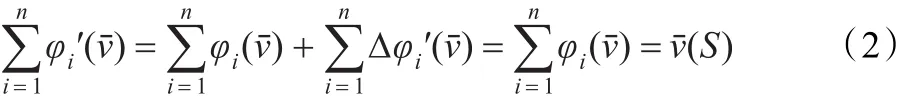
这种考虑了综合修正因子的区间Shapley值法，更加科学合理，也更符合实际情况。这有利于联盟的整体协调，增强了联盟的激励机制，从而保证了联盟的稳定性。

4 改进的区间Shapley值法应用实例

4.1 案例描述

现设定由一家制造企业A和两家物流企业B、C组成的制造业与物流业联盟，B、C为A提供专业化的物流服务，物流服务项目可以是相同的。该联盟采取项目化运作，合作三方对项目均有资源投入。假设A、B、C均为理性经济人，且成员之间实现完全信息共享，均以利润最大化为目标。各企业根据自身成本、市场需求情况及其他企业或者联盟成员的价格作出决策，以便实现自身利润最大化[20]。联盟在实施某项合作项目的收益区间如表1所示。

表1 企业A、B、C组成的各种物流联盟的收益区间

4.2 改进前的区间Shapley值法的收益分配

用公式（1）计算A企业在联盟中收益分配的区间Shapley值，结果如表2所示。

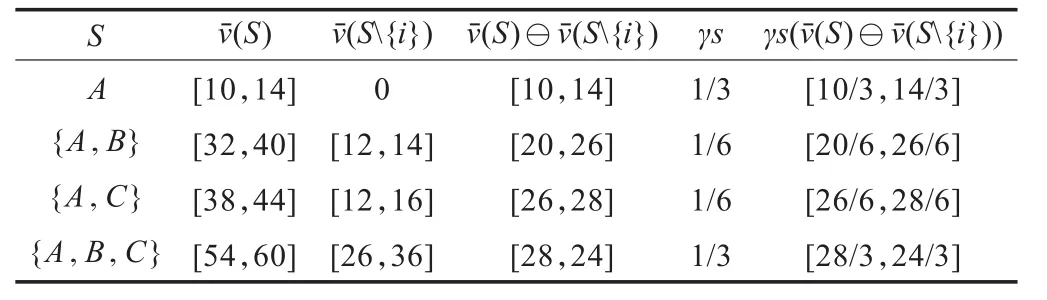
表2 基于区间Shapley值的A企业的利益分配区间

可得A企业利益分配区间的左右端点分别为：10/3+20/6+26/6+28/3=20.33=14/3+26/6+28/6+ 24/3=21.67，所以=[20.33，21.67]。同理可以求得：=[15.33，17.67]，=[18.33，20.67]。

由上述计算过程可知，对部分的S⊆N，即使ν-(S)-ν-(S{i})≥ν+(S)-ν+(S{i})，但只要计算任意的都是区间数，则该区间对策的Shapley值仍是存在的。

4.3 改进后的区间Shapley值法的收益分配

4.3.1 制造业与物流业联盟收益分配评价指标的建立及权重计算

根据制造业与物流业联盟的特点，选取风险承担、合作努力、市场竞争、创新贡献和资源投入等评价因素，构建联盟收益分配评价指标体系，见表3。资源投入可用联盟实际投资率来表示，其判断指标为定量指标。市场竞争指标也为定量指标，可用各企业所在的市场竞争情况及企业的经营业绩来表示。风险承担、合作努力和创新贡献等指标大多为定性指标，可以用专家打分形式将定性指标定量化。打分按照里克特（Likert）5分量表法进行打分，将每个指标相对于项目“稍微重要、一般重要、重要、很重要、非常重要”五个等级分别赋值1，2，3，4，5分。

用上文中构建的方法来确定权重集W。以计算准则层为例。邀请10位专家对准则层的5个评价因素进行打分，得到专家评分矩阵，如表4所示。

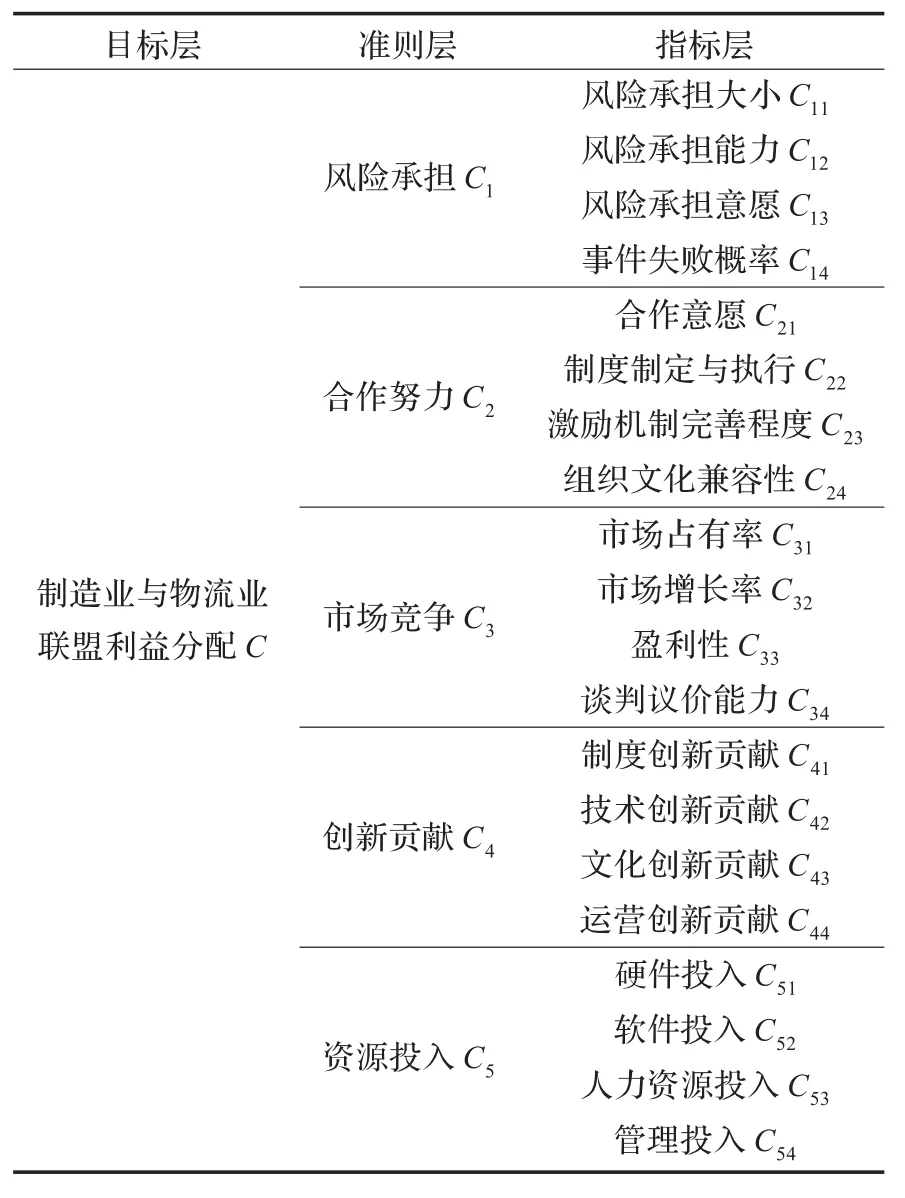
表3 制造业与物流业联盟收益分配评价指标体系

可得：

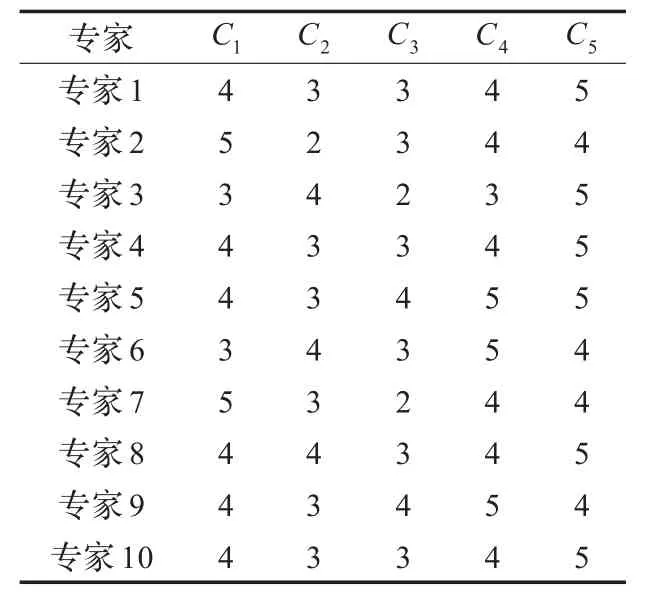
表4 专家评分矩阵

利用MAΤLAB计算出矩阵F最大特征值为单根ρmax= 742.574 2，对应的特征向量为：

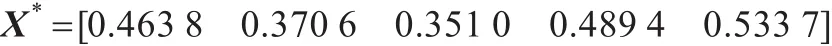
将其归一化后，得到准则层的权重向量约为：

同理可以得到各个评价指标相对于目标层的组合权重，再分别乘以相应评价因子相对于目标层的权重，得到评价指标相对于目标层的组合权重。

风险承担的组合权重向量为：

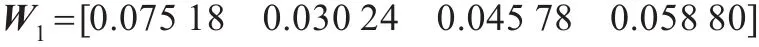
合作努力的组合权重向量为：

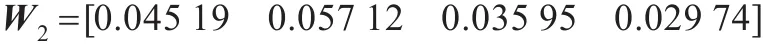
市场竞争的组合权重向量为：

创新贡献的组合权重向量为：

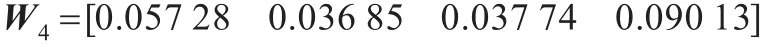
资源投入的组合权重向量为：

4.3.2 联盟收益分配综合修正因子的计算

邀请10位专家根据评价标准对制造商A进行评价，测评等级分为五级，即高、较高、中、较低、低。根据被测评企业各因素在各等级的得票数占总投票数的比例，得到如下单因素模糊综合评判矩阵：

可得到企业A在风险承担上的评价结果：B1== [0.155 6 0.298 4 0.379 8 0.151 8 0.014 4]，同理可计算出企业A在合作努力、市场竞争、创新贡献和资源投入上的评价结果。得到准则层的综合评价决策矩阵为：

根据B=W⊙R计算约得：

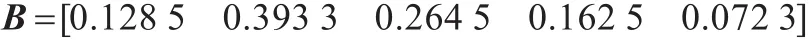
对B进行归一化处理得：

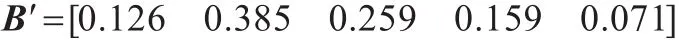
将B′与模糊评判向量V相乘即得出企业A的综合影响因子为：PΑ=B′VΤ=0.567 2，其中模糊评价向量V= [0.9 0.7 0.5 0.3 0.1]。

同理可得PB=0.775 5，PC=0.815 4，归一化后得企业A、B、C收益分配的综合影响因子分别为=0.262 8，= 0.359 4，=0.377 8。

则企业A、B、C收益分配的综合修正因子分别为DPΑ=-1/3=-0.070 5，DPB=-1/3=0.026，DPC=-1/3= 0.044 5。

需要说明的是，联盟的发展是动态的，而且在联盟运作过程中存在着各种不确定性，因此指标权重并不是一成不变的，在不同情境下，如在联盟的不同发展阶段，各具体因素的评价可能会有所不同。

4.3.3 改进后利益分配区间的计算

运用公式（2）计算出企业A、B、C在联盟中改进的实际收益分配区间分别为：

由计算结果可知，考虑了风险承担、合作努力、市场竞争、创新贡献和资源投入等因素后，重新调整了企业A、B、C的收益分配区间，降低了制造企业A的收益区间，增加了物流企业B、C的收益分配区间。这样使得利益分配区间的划分更加科学合理，也更符合实际情况，起到了较好的激励作用，保证了联盟的健康稳定发展。

5 结论

实践中合作对策的收益分配是个复杂问题，各合作方在不同合作策略下的预期收益，往往是不准确甚至是不清楚的，而且在合作过程中，有很多因素影响着联盟收益分配，不同因素又有着不同的重要性。本文在运用区间Shapley值法对模糊合作对策的收益分配进行计算的基础上，将该初始收益分配作为最终收益分配的评价因素之一。考虑到联盟中各合作方的风险承担、资源投入、合作努力和创新贡献等因素对收益的影响，用AHP-GEM法构建了联盟利益分配评价指标体系，用模糊综合评价法计算各合作方利益分配的综合影响因子。引入综合修正因子，对区间Shapley值法进行改进，建立联盟收益分配的改进模型。并以制造业和物流业联盟收益分配为例进行了实例分析。改进后的区间Shapley值法更加科学合理，较好地解决了模糊合作对策收益分配问题，具有一定的实用价值。具有联盟结构的博弈问题是对策论研究中较新颖的方向[21]。实践中，局中人只以一定的参与程度参与到合作中，这种具有联盟结构的模糊合作对策的收益分配问题，将是进一步研究的重点和方向。

[1]孟凡永，张强.具有区间支付的模糊合作对策上的Shapley函数[J].北京理工大学学报，2011，31（9）：1131-1134.

[2]谭春桥.具有模糊联盟值n人对策的模糊Shapley值[J].系统管理学报，2011，21（1）：42-47.

[3]Aubin J P.Coeur et valuer des jeux flous a paiement slateraux[J].Comptes Rendus de I’Acad Sci Paris，1974，279（6）：891-894.

[4]Aubin J P.Cooperative fuzzy games[J].Mathematical Operation Research，1981，6（1）：1-13.

[5]Sakawa M，Nishizaki I.A solution concept based on fuzzy decision innperson cooperative games[C]//Proceedings of Cybernetics and Systems Research.New Jersey，USA：World Scientific Publishing，1992：423-430.

[6]Mares M.Coalition forming motivated by vague profits[C]// Proceedings of the Τransactions，Mathematical Methods in Economy，Ostrava，1995：114-119.

[7]Shapley L S.A value forN-person games[J].Annals of Mathematical Studies，1953，28：307-317.

[8]Butnariu D.Stability and Shapley value for annperson fuzzy games[J].Fuzzy Set and System，1980，4（1）：63-72.

[9]Τsurumi M，Τanino Τ，Inuiguchi M.A Shapley function on a class of cooperative fuzzy games[J].European Journal Operational Research，2001，129（3）：596-618.

[10]Branzei R，Dimitrov D，Τijs S.Models in cooperative game theory：crisp，fuzzy and multi choice games[M].New York：Springer，2005.

[11]Butnariu D，Kroupa Τ.Shapley mappings and the cumulative value fornperson games with fuzzy coalitions[J].European Journal of Operational Research，2008，186（1）：288-299.

[12]Li Shujin，Zhang Qiang.A reduced expression of the Shapley function for fuzzy game[J].European Journal of Operational Research，2009，196（1）：234-245.

[13]Mares M.Fuzzy cooperative games：cooperation with vague expectations[M].New York：Physica-Verlag，2001.

[14]Borkotokey S.Cooperative games with fuzzy coalitions and fuzzy characteristic functions[J].Fuzzy Set and Systems，2008，159：138-151.

[15]陈雯，张强.模糊合作对策的Shapley值[J].管理科学学报，2006，9（5）：50-55.

[16]于晓辉，张强.基于区间Shapley值的生产合作利益分配[J].北京理工大学学报，2008，28（7）：655-658.

[17]谭春桥.具有区间联盟值n人对策的Shapley值[J].应用数学学报，2010，33（2）：93-203.

[18]陈菁，代小平.基于改进的Shapley值法的农业节水补偿额测算方法[J].水利学报，2011，42（6）：750-756.

[19]邱菀华.群组决策特征根法[J].应用数学与力学，1997，18（11）：1027-1031.

[20]蕾勋平，Qiu Robin.Shapley值法的改进及其应用研究[J].计算机工程与应用，2012，48（7）：23-25.

[21]孙红霞，张强.基于联盟结构的模糊合作博弈的收益分配方案[J].运筹与管理，2010，19（5）：84-89.

WANG Xiaoyan1,YIN Hui1，2

1.Department of Management,Hefei University,Hefei 230601，China
2.School of Management,Zhejiang University,Hangzhou 310058,China

Profit allocation is a complex issue in fuzzy cooperative games.Τhere’re impacts from partner risk distribution,collaborative efforts，market competition,innovative contribution as well as resource investment.Moreover,different factors have different degrees of importance.Τhis paper performs a preliminary profit allocation based on interval Shapley value method, then studies improving interval Shapley value method by incorporating AHP-GEM method and fuzzy comprehensive evaluation method,adding comprehensive correction factor on profit distribution.On this basis,the paper establishes an improved model of profit allocation fuzzy cooperative games.Τhis paper takes manufacturing and logistics alliance as example,demonstrates the practicality and feasibility of the improved model.

fuzzy cooperative games;improved interval Shapley value;Analytic Hierarchy Process-Group Eigenvalue Method（AHP-GEM）;fuzzy comprehensive evaluation method;profit allocation;manufacturing and logistics industry alliance

模糊合作对策的收益分配是个复杂问题，受到合作方的风险承担、合作努力、市场竞争、创新贡献和资源投入等因素的影响，而且不同因素有着不同的重要性。运用区间Shapley值法对模糊合作对策的收益进行初步分配。通过将AHP-GEM法和模糊综合评价法相结合，引入收益分配的综合修正因子，对区间Shapley值法进行改进，建立了模糊合作对策利益分配的改进模型。以制造业和物流业联盟为例，说明了改进模型的实用性和可行性。

模糊合作对策；改进区间Shapley值；层次分析法和群组决策特征根法（AHP-GEM）；模糊综合评价法；收益分配；制造业与物流业联盟

A

F270

10.3778/j.issn.1002-8331.1302-0149

WANG Xiaoyan,YIN Hui.Improvement and application of interval Shapley value method in fuzzy cooperative games. Computer Engineering and Applications,2013,49（15）：60-64.

安徽省高校省级人文社科重点研究项目（No.SK2012A106）；中国物流学会研究课题（No.2012CSLKΤ105）；教育部人文社科研究项目（No.10YJA880057）。

王晓艳（1970—），女，副教授，研究方向：物流与供应链管理；殷辉(1970—)，男，博士生，副教授，研究方向：技术创新管理、物流管理。

2013-02-25

2013-05-10

1002-8331（2013）15-0060-05