IGS精密星历内插及外推方法比较分析＊

刘 翔，时振伟

（山东科技大学 测绘科学与工程学院，山东 青岛266590）

0 引 言

国际GNSS服务（IGS）发布的GPS精密星历采样间隔为15min，在实际定位中需要间隔更小的数据，这就需要高精度、快速地对精密星历进行内插或外推。目前，利用IGS精密星历求任意时刻卫星坐标的方法可分为插值法和拟合法两类方法，而且已有大量文献阐述了这两类方法。只要选择合适的阶数，插值点的位置等条件就能到得到很好的内插精度，但外推精度有限。由于IGS精密星历仅给出每天00∶00∶00－23∶45∶00的星历数据，为了得到23∶45∶00－24∶00∶00的星历数据，有两种方法：一是将当天的精密星历与下一天的“拼接”，这样就可以沿用内插方法；二是仅用当天的精密星历进行外推［1]。前一种方法需要收集处理更多的精密星历数据，特别是当两天的精密星历中出现某颗卫星的数据中断的情况，则该方法失效，必须依赖第二种方法。而要使用第二种方法，则必须提高星历外推的精度。

简要介绍了三角插值的基本模型，及卫星在惯性坐标系和地固系的实际运动特点，Lagrange插值和Chebyshev拟合的数学模型在很多文献中都有涉及［2－5]，这里不再阐述。用 Matlab编制程序实现了这些插值方法，通过精密星历内插及外推卫星位置的实际算例，对精度进行分析，得到了一些有意义的结论，证明了由于顾及了卫星的实际运动特点，三角插值在精密星历外推能力方面优于Lagrange插值和Chebyshev拟合。

1 GPS卫星运动特点及三角函数插值算法

1.1 卫星运动特点

IGS给出的精密星历是以地固系为空间基准的，是在ITRF参考框架内的。以2012年8月6日PRN01卫星为例，图1和图3分别示出了其在地固系和惯性坐标系下的运动特点，图2和图4分别示出了卫星的运动轨迹，其他GPS卫星的运动特点与此类似。图1中，一天内除了Z坐标分量表现较好的12h周期性（GPS卫星轨道周期为11 h 58min）外，X和Y都是较复杂的曲线；图2中卫星在地固坐标系下的三维运行轨迹不太规则，主要是因为在地心地固坐标系中，卫星的坐标还要受坐标旋转框架的影响，而惯性坐标系的坐标框架是非旋转的［6]，所以图3中，X、Y、Z 三坐标分量都表现出约12h周期性。图4中卫星在惯性坐标系下的三维运行轨迹较为规则，近似为椭圆形。

GPS卫星在地固系和惯性坐标系下的基本运动特点不同的根本原因，是由于在地固系下给出的卫星星历引入了地球本身的运动，包括自转、岁差、章动、极移等，由此影响了卫星自身运动的规律。

而在惯性坐标系下描述卫星运动，则更能反映卫星本身的运动特点，更有规律可循［6]。

1.2 三角函数多项式插值算法

基于轨道坐标的这个特征，可以利用基于三角函数多项式来进行插值，多项式的形式为［7]：

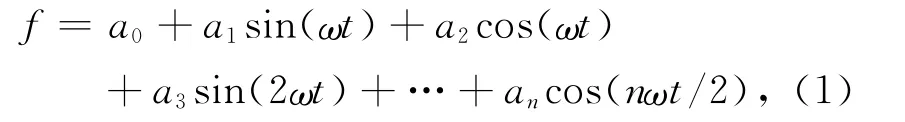
式中：f为卫星的坐标分量x，y，z；ω为频率因子，ω＝2π／T；T 为GPS卫星运行周期；a0，a1，a2…an为待求系数；n为三角函数的项数（插值阶数）；t为对应历元时刻。根据卫星的运动周期，对于惯性坐标系下的轨道，运用基于三角函数多项式的插值方法反映了卫星位置在坐标框架下的周期特性，可能会使插值精度更高。当然先把精密星历中的坐标转换成惯性坐标系下的坐标，转换公式为［6，8]

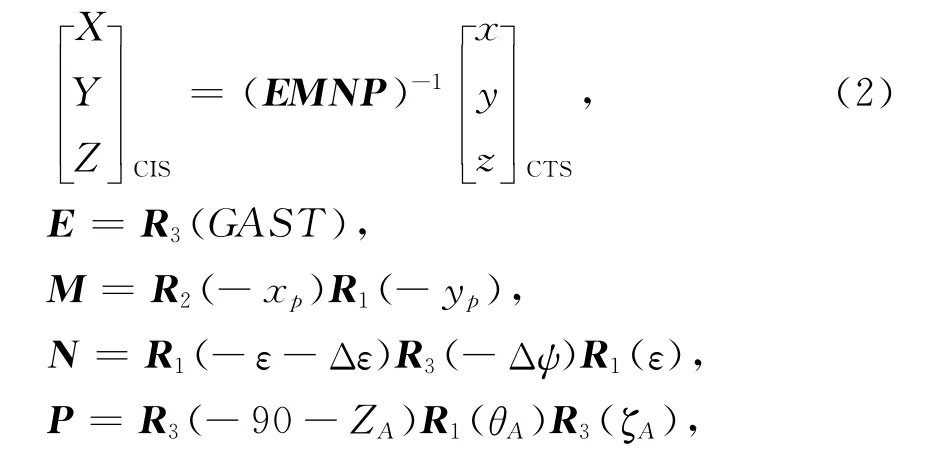
式中：E为旋转真春分点时角；M为极移旋转矩阵；N为章动旋转矩阵；P为岁差旋转矩阵；（x，y，z）TCTS为以协议地极方向CTP为指向的协议地球坐标；（x，y，z）TCTS协议天球坐标系；R1，R2，R3分别为旋转矩阵；GAST为真春分点的格林尼治时角；xp，yp为极移分量；ε，Δε，Δψ 分别为黄赤交角、交角章动和黄经章动；ZA，θA，ζA称为岁差参数。

根据上述公式得到惯性坐标系坐标，求出待求系数，基于所要插值的时间，得到实时惯性系坐标，完成插值后，再转换到地固系即可。

2 计算实例及结果比较

2.1 内插精度分析

在IGS官方网站上下载SP3精密星历文件，选取2012年8月6日的SP3精密星历文件作为实验数据，历元时刻为00∶00∶00－23∶45∶00.采用对称内插的方法，计算时取30min间隔的历元作为内插点计算各个内插时间段中间时刻的卫星位置，以便将内插得到的卫星位置同精密星历给出的卫星位置进行比较。在Matlab7.1环境下实现得到1号卫星7阶～25阶的内插结果，IGS向全球GPS用户提供的GPS精密星历，其误差一般小于5cm，所以这几种内插精度至少要小于5cm.

表1示出了Lagrange插值、Chebyshev拟合、三角函数插值的7阶～25阶的标准差，图5～7示出了三种方法的标准差折线，图8示出了这三种方法在X方向不同阶次插值效果比较。

表1 三种方法不同阶次插值标准差

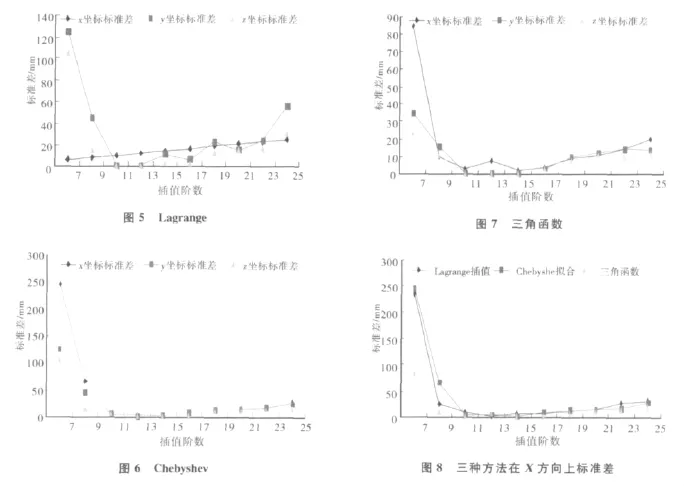
从表1可以看到，用Lagrange插值时，当阶数取13时，内插精度最高，X，Y，Z3个坐标的最大标准差为3.23mm；用Chebyshev拟合时，阶数为15时，内插精度最高，X，Y，Z3个坐标的最大标准差为3.45mm；用三角函数多项式插值时，当阶数取15时，内插精度最好，X、Y、Z3个坐标的最大标准差为2.13mm.对比两表可以发现，三角函数多项式插值，从7阶到25阶，各项误差指标变化不大，但是Lagrange插值及Chebyshev拟合的标准差随着阶数的不同有变化相对较大。

在插值时只选择了在中间时刻的插值，如选择的插值位置不同，则会有不同的精度，用Lagrange插值及Chebyshev拟合卫星位置，无论选用多少阶，内插的卫星位置图呈现U型结构，即出现了最小值区域。在插值过程中，当插值点位于节点的两端时，插值精度更低。

2.2 外推精度分析

选取PRN为1号的卫星在2012年8月6日23h45min 00s的卫星坐标为外推起点，推15 min，到24h00min 00s，与8月7日00h00min 00s的精密星历坐标比较，表2分别示出了三种方法不同阶次的外推误差。

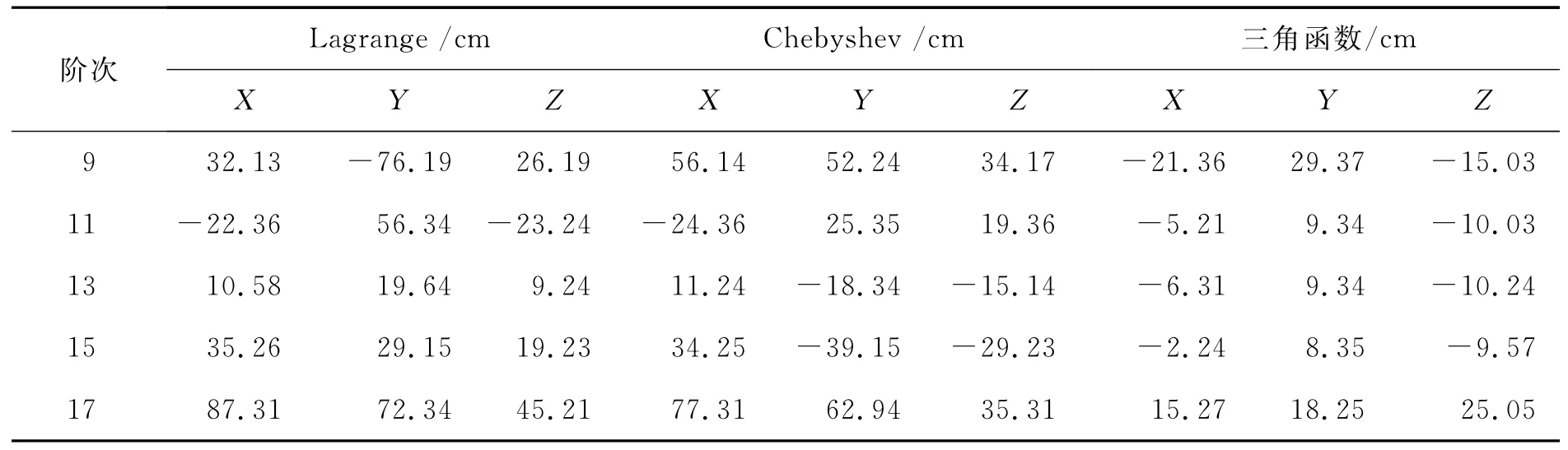
表2 三种不同方法的不同阶次预测误差

从表2可以看出，Lagrange插值的外推精度在13阶时插值误差最小，在24h00min 00s时的最大误差达到19cm；Chebyshev的外推精度在13阶插值误差最小，在24h00min 00s最大误差达到－18cm；在三角函数多项式插值的外推精度在15阶时插值误差最小，在24h00min 00s时的最大误差达到－10cm.

通过以上分析，Lagrange多项式插值及Chebyshev拟合由于未考虑卫星的实际运动特点，当待插值点位于节点数据两端时，内插精度会下降；而三角函数多项式插值由于考虑了卫星的实际运动特点，可以从一定程度上克服这一问题，外推精度要明显优于前两种方法，这是因为后者有效地利用了卫星在空间的运动特点，使得其插值函数更符合卫星的实际运动。

3 结 论

三种插值方法在对精密星历进行内插时，只要选择的插值阶数合适以及插值点的位置合适，精度相当，都可以达到毫米级，因此无论采用哪种方法进行内插，都可以取得满意的结果，但是三角函数多项式插值比Lagrange插值及Chebyshev拟合更稳定。在精密星历外推时，三角函数多项式插值的精度要高于Lagrange插值及Chebyshev拟合，因此应避免用Lagrange插值及Chebyshev拟合进行外推。通过上文的误差分析可知，仅采用观测数据当天的精密星历，利用三角函数多项式插值获得观测数据对应的精密卫星位置，其插值精度足以满足一般的动态单点定位要求。

［1]刘伟平，郝金明，李作虎.由广播星历解算卫星位置、速度及精度分析［J].大地测量学地球动力学，2010，30（2）：144－147.

［2]刘大杰，陶本藻.实用测量数据处理方法［M].北京：测绘出版社，2004.

［3]孟大志，刘 伟.现代科学与工程计算［M].北京：高等教育出版社，2009.

［4]魏二虎，柴 华.GPS精密星历插值方法比较研究［J].全球定位系统，2006，31（5）：13－15.

［5]孔巧丽.用Chebyshev多项式拟合GPS卫星精密坐标［J].测绘通报，2006，31（8）：1－3.

［6]孔祥元，郭际明，刘宗泉.大地测量学［M].武汉：武汉大学出版社，2008.

［7]张守建，李建成，邢乐林，等.两种IGS精密星历插值方法的比较分析［J].大地测量与地球动力学，2007，27（2）：80－83.

［8]张 勤，李家权.GPS测量原理及应用［M].北京：科学出版社，2009.