GPS伪距单点定位程序实现若干问题＊

李鹤峰，党亚民，王世进，3，王霞迎

（1.中国测绘科学研究院大地测量与地球动力研究所，北京100830；2.山东科技大学测绘科学与工程学院，山东 青岛266510；3.辽宁工程技术大学测绘与地理科学学院，辽宁 阜新123000）

0 引 言

在全球卫星导航系统（GNSS）的数据处理中，伪距单点定位是经常涉及的问题，并广泛应用于实时位置导航和为RTK提供实时卫星位置和钟差等信息［1－3]。作为GNSS最具代表性的全球定位系统（GPS），国内外学者有非常多的研究，伪距单点定位技术已经相当成熟。但作者在研究中发现，定位程序的编写在相当多的文献中仅一笔略过，对学习GPS编程中遇到问题的读者造成很大的困扰，浪费大量研究的时间去摸索程序的编写。选取GPS系统，基于Visual C＋＋平台，编写伪距单点定位程序，详细研究伪距单点定位的原理、算法及程序实现过程，重点就程序编写过程中的关键部分和易于出错之处总结了详细的解决思路，通过算例计算分析，验证了问题解决的正确性和程序编写的合理性。

1 伪距单点定位

1.1 定位原理

GPS伪距定位是通过空间距离的后方交会来实现，如图1所示。理论上通过测算三颗卫星到用户的距离，组成三元方程组，从而计算出用户的三维坐标。实际应用中由于接收机钟差难以预先准确确定，通常将其看作一个未知参数，与用户三维坐标一并求解。这时需要第四颗卫星参与解算，组成四元方程组，进而精确计算出用户的三维坐标［2］。

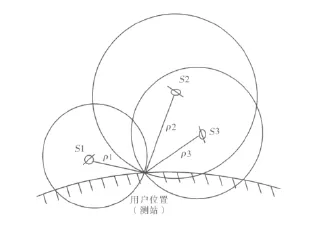
图1 伪距定位原理

设t在时刻用户测站点到S1，S2，S3，S4四颗卫星的伪距观测值为ρj，j＝1，2，3，4，通过卫星导航电文解算，译出该时刻四颗卫星的三维地心坐标（Xj，Yj，Zj），j＝1，2，3，4.用上述空间距离后方交会的定位原理，计算用户位置的三维地心坐标（X，Y，Z），伪距观测方程为

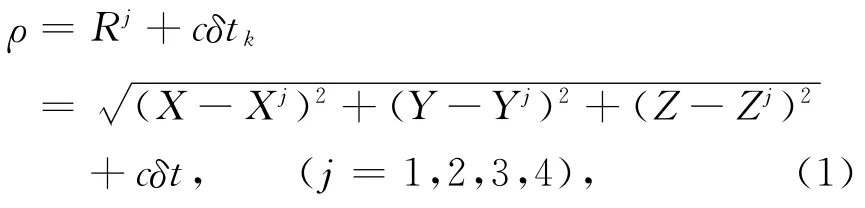
式中：假设伪距观测量ρj已经通过星历中的电离层、对流层改正和卫星钟差改正；Rj为接收机天线相位中心到卫星天线相位中心的几何距离；c为光速；δtk为接收机钟差。

1.2 数学解算模型

式（1）为方便理解伪距定位原理，假设卫星钟差、电离层和对流层延迟均已改正过。在定位解算中，考虑到这些误差改正，伪距观测方程式（1）改写为

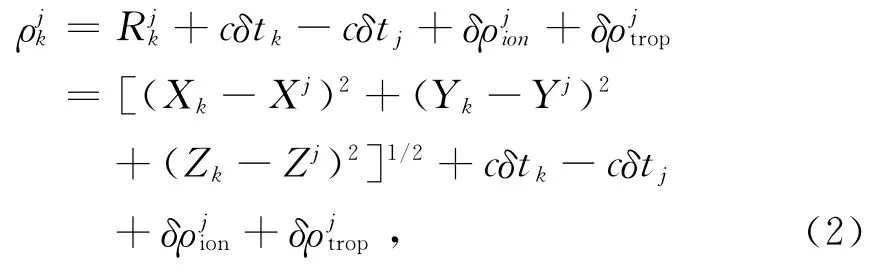
实际解算中，可以从观测文件提取接收机的近似坐标 （X0，Y0，Z0），令 （δx，δy，δz）为接收机坐标的改正值，将式（2）在近似坐标 （X0，Y0，Z0）处用泰勒级数展开，取一次微小项，得线性化伪距观测方程：

式中：

这些都可以根据已知值计算出结果，卫星钟差δtj可以根据δtj＝af0＋af1（tc－toe）＋af2（tc－toe）2进行修正（af0，af1，af2，toe从卫星广播星历中读取，tc为卫星发射信号时刻，通过计算求得），电离层延迟可以通过双频观测消除，对流层延迟可以通过模型进行改正，所以，令常数项部分－δρjtrop＝Lj，四个未知数，需要四个观测方程，将式（3）写为矩阵形式：

式中：

根据最小二乘法求得改正数δX ＝ （ATA）－1ATL.求出δX＝［δxδyδzcδtk］T后，即可按

求出接收机位置坐标 （Xk，Yk，Zk）.

2 程序实现中问题及解决思路

根据上述GPS单点定位原理，基于Visual C＋＋平台，编写单点定位程序，程序设计流程如图2所示。

由于在GPS单点定位程序编写过程中，需要用到不少函数的调用及矩阵循环计算，数值分析，具体程序代码较长且繁琐，这里就程序实现中的关键点也是易于出错点给予详细的解决思路。

1）伪距电离层改正

伪距的电离层改正一般采用双频观测消除。GPS信号中的C1，P1，P2测距码调制在L1，L2载波上 （L1－C1，L1－P1，L2－P2），但是N 文件中用于电离层改正的伪距观测数据类型（C1，P1，P2），并不是在每个历元中出现的情况相同，为了达到最好的改正效果，就要有选择的去利用，程序实现时要分情况考虑，优先选择伪距观测值P1，P2组合为

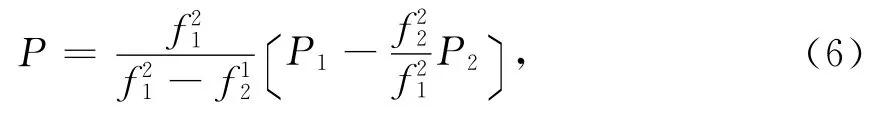
式中：P为双频改正后的伪距值；f1，f2为L1，L2载波频率。没有P1情况下使用C1，P2组合，如果没有P2或同时没有C1，P1的情况下，就不能使用双频观测对电离层进行消除，需要另行考虑在单频情况下的电离层模型改正。

图2 GPS伪距单点定位程序设计流程图

2）参考星历选取

GPS星历每2h播发一次，卫星发射信号时刻与星历播发时刻相同的概率极小，所以计算卫星位置时，要选取最近的星历作为卫星发射时刻的参考去计算卫星坐标。程序实现时，由于卫星信号传播的时间非常短（0.07s左右）［2]，可以用观测 O 文件中的时间t0与广播星历N文件中的时间tn求差值δt＝fabs（t0－tn）.当δt≤3 600s时，该时刻tn的广播星历即可作为参考用于计算观测时刻tn对应的卫星坐标。

3）卫星发射信号时刻归化

GPS时间系统采用原子时秒长作为时间基准，起算原点为1980年1月6日（星期日）0时0分0秒的协调世界时（UTC）.广播星历中播发的参考时刻toe是去除GPS整周数后不满一周总秒长，GPST整周数的总秒长，而参与解算卫星位置的时间tk（归化时间）是发射时刻tc相对于参考时刻toe的秒长，即tk－tc－toe.编写程序时，要考虑到周的开始和结束，计算出tk后要对其进行如下判断调整，如tk＞302400，那么tk＝tk－604800；如tk＜－302400，那么tk＝tk＋604800，302 400为半周的秒长，一周共604 800s.

4）偏近点角迭代计算

根据卫星轨道的偏近点角公式Ek＝Mk＋esinEk（平近点角Mk，卫星轨道偏心率e都已知），由于e非常小，sinEk＜1，故esinEk是一个微小值。可用程序通过迭代法实现Ek的快速求解，令Ek＝Mk连续回代求新的Ek，直到合适的精度停止迭代。截取C＋＋程序片段如下：

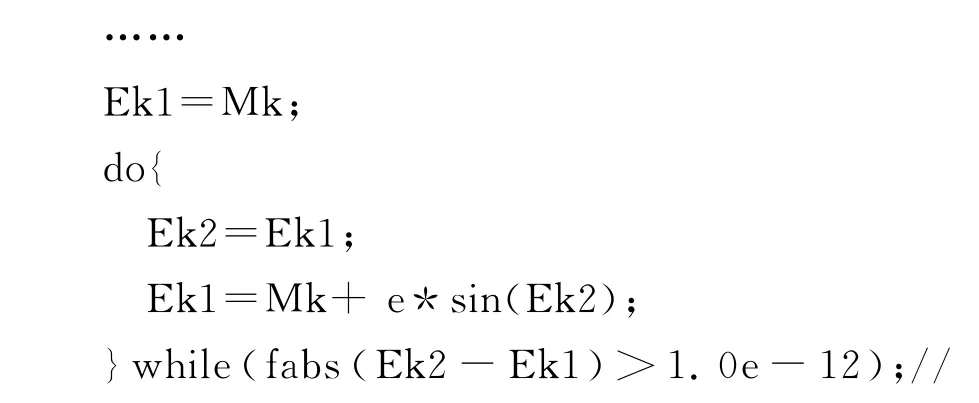
10－12为经验值，取该值可以达到需要的收敛效果

Ek＝Ek1；／／迭代出偏近点真值

……

5）真近点角象限的判断

真近点角计算式：

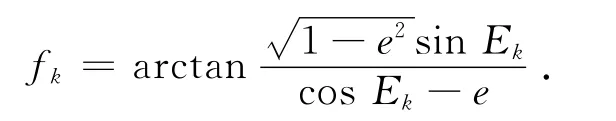
在程序的编写过程中是最容易出错的地方，其主要原因是用反正切函数没有考虑fk所在的象限，若要通过程序正确计算fk，需要联合考虑cos fk＝与值的符号，以确定fk所在的象限。截取C＋＋程序片段如下：

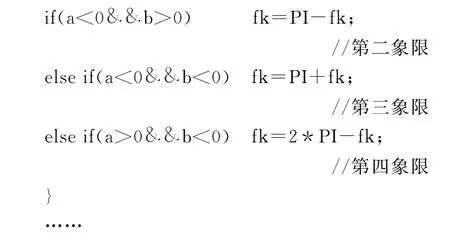
6）地球自转改正

式中：ω为地球自转角速度；t为信号传播时间。

3 算例分析

本算例选用2012年1月5日河北某已知基准点的实验数据，观测采用双频GPS接收机，时间为7h41min 10s－8h51min 10s，共1h10min的GPS观测数据，接收机采样率为10s采集一次数据。根据编写的C＋＋单点定位程序，计算接收机坐标，并将程序计算值与基准站已知坐标值对比求差，各分量的差值如图3所示。

从图3可以看出，通过1h10min的GPS连续观测数据，用上述解决思路编写的伪距单点定位程序解算基准点坐标，将解算值与已知基准点坐标值求差，结果X分量的差值在9m以内，Y分量的差值大都在15m以内，Z分量的差值在5m以内，表1示出了定位结果各分量残差中误差RMS统计分析表（坐标数据考虑到涉密问题仅取小数点前4位）。

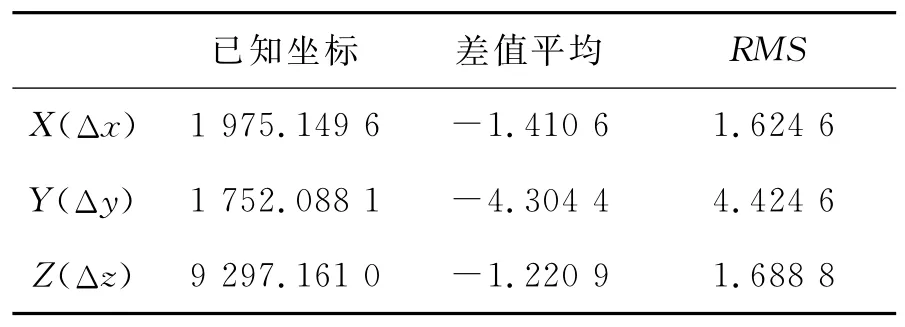
表1 定位结果统计分析（单位：m）

由于主要着重解决程序编写中易于出现的上述问题，所以程序在编写过程中没有考虑多路径效应，接收机天线相位中心改正以及相对论效应等。但从定位结果图和统计分析表可以看出，定位结果在5m以内，完全可以验证GPS伪距单点定位解算结果的正确性，从而验证了上述程序编写中易于出错点问题解决的合理性。

4 结 论

充分考虑各种误差影响（电离层、对流层延迟，卫星、接收机钟差，地球自转改正，多路径、接收机天线相位中心改正等），GPS单点定位精度一般在10m以内。虽然目前精密单点定位静态已实现mm～cm级精度，动态精度也达到cm～dm级［7－8]，但是，由于GPS精密星历在11天后才能得到，对实时导航定位没有太大意义。利用实时GPS广播星历进行伪距单点定位，可以广泛开展实时动态定位，对实现船只、飞机和车辆等各种运动目标的导航定位，监控管理具有重要意义。因此GPS伪距定位的研究不会过时，单点定位的原理和程序的编写就尤为重要，更是学习和研究GNSS的基础。

［1]徐绍铨，张华海，杨志强，等.GPS测量原理及应用［M].2版，武汉：武汉大学出版社，2003.

［2]党亚民，秘金钟，成英燕.全球导航卫星系统原理与应用［M].北京：测绘出版社，2007.

［3]廖 华.GPS伪距单点定位算法的综合比较［J].测绘科学，2011，36（1）：20－21.

［4]朱 勇，方源敏，刘建忠.基于双频P码的GPS伪距单点定位研究及精度分析［J].海洋测绘，2008，28（7）：15－18.

［5]何晓薇，牟其锋，向淑兰.GPS信号的电离层延迟误差及改正［J].中国民航飞行学院学报，2008，19（1）：16－18.

［6]龚佑兴.GPS单点定位研究［D].长沙：中南大学，2004.

［7]张金宝，王少闵.GPS精密单点定位程序设计与实现［J].城市勘察，2009（5）：60－62.

［8]CAI Changsheng，GAO Yang.Precise point positioning using combined GPS and GLONASS observations［J].Journal of Global Positioning Systems，2007，6（1）：13－22.