GNSS导航中GDOP最小值的分析与验证*
李 森,李长会,刘 宁,杨 昊
(61365部队,天津300140)
0 引 言
GNSS导航定位的误差取决于观测量的精度和接收机—卫星几何分布的情况,精度衰减因子GDOP描述了接收机与可视卫星间的几何分布关系,反映了由于卫星几何关系的影响造成的伪距测量误差与目标位置误差的比例系数[1],是衡量卫星定位精度的一个重要指标。几何分布越好,GDOP值就越小,定位精度就越高。因此为了提高GNSS导航定位的精度,应使GDOP值最小[2-3]。
文献[4-6]给出了GDOP 值与接收机和卫星组成的多面体体积之间的关系,但是未对GDOP的最小值进行分析;文献[7]对GPS定位中的GDOP进行了分析,推导出了利用4颗卫星导航定位时,GDOP的最小值为;文献[1]经过分析发现文献[7]给出的最小值是不能达到的,并利用矩阵的特征值推导出GDOP的理论最小值为文献[8][9]从不同角度得到了与文献[1]相同的GDOP理论最小值及其计算公式。以上文献在GDOP最小值讨论方面均有一定的参考价值。但是分析发现文献[8]和[9]给出的GDOP最小值计算方法是从纯数学角度推导的,没有考虑到接收机不能接收地平线以下卫星信号的情况。文献[10]也指出在卫星导航定位中,接收机通常只能接收卫星高度截止角大于零的卫星信号,在实际中上述理论最小值不能达到,但文献[10]并没有给出实际GDOP最小值的求解方法。
对现有文献中GDOP最小值的计算方法进行了讨论,分析和给出了其计算GDOP最小值的不合理原因;从实际情况出发,对GDOP最小值的求解重新进行了分析和推导,得到了GDOP最小值的计算方法,并给出了GDOP值达到最小时的卫星空间几何分布情况;最后给出了仿真和实测算例,验证了本文推导方法和结果的正确性。
1 现有GDOP最小值计算方法的分析
1.1 GDOP的定义
接收机至卫星i在历元tk时刻的伪距观测方程为

式中:ρ为伪距观测值;D为测站至卫星的几何距离;c为真空中光速;δti,δt为接收机与卫星钟差;dion为电离层延迟;dtro为对流层延迟;ε为未模型化的残余误差项及观测噪声。
在接收机的概略位置¯rtro=(x0y0z0)T处泰勒展开,忽略二阶以上的小量,得到观测n(n≥4)颗卫星的观测方程为

式中:X=(δxδyδz b)T为待估向量;(δxδyδz b)T为位置改正量;b为接收机钟差等效距离参数;为n×4的列满秩系数矩阵;ei=(exi,eyi,ezi)为接收机指向第i颗可视卫星的方向余弦,满足|ei|=1,即ei(i=1,2,…,n)均位于单位球面上;L为n×1观测向量,其权阵为单位矩阵;ε为n×1随机误差向量。
模型(2)中X的最小二乘解为

其协方差阵为Q=σ20(HTH)-1,其中σ0为未知的单位权中误差,

则 GDOP=[tr(HTH)-1]1/2其中tr(HTH)-1表示矩阵(HTH)-1的迹。
GDOP表征了接收机和可视卫星在空间的几何分布情况。GDOP值最小,则接收机和卫星的空间几何分布最佳,定位精度最高。另外,随着可视卫星数目的增加,GDOP的最小值不断减少,即可视卫星数目越多,GDOP 值越小,定位精度越高[9-10]。
1.2 现有GDOP最小值计算方法的分析

由条件|ei|=1,i=1,2,…n,可知矩阵HTH的迹为

即

当λi(i=1,2,3)相等时式(6)的等号成立且当λ4=n时,获得最小值文献[9]在条件下得到了同样的GDOP最小值。但是这个最小值的获取有一个前提就是要求HTH为对角矩阵,即需要同时满足以下条件
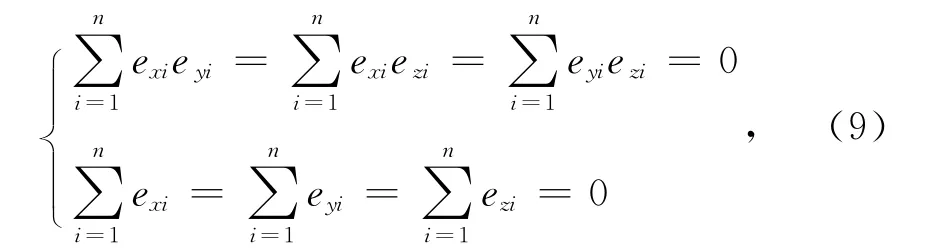
由于参与导航定位解算的卫星均应为地平面上方的可视卫星,则所有卫星与z轴的夹角介于0和之间,故要求e>0,i=1,2,…,n.这与条件zi相矛盾,所以矩阵HTH不能为对角矩阵。故上述GDOP最小值是数学意义上的最小值,而不是测量意义上的最小值。
2 GDOP最小值的理论推导
推导GDOP的最小值,需要在满足ezi>0,i=1,2,…,n的条件下进行,此时HTH不再是对角矩阵。经过分析,给出如下结论:

证明:因H为列满秩矩阵,则HTH是正定矩阵,故C、D也是正定矩阵。即,在矩阵偏序意义下满足C>0、D>0.
由分块矩阵的求逆法可知

由于C、D为正定矩阵,故UD-1UT和UTC-1U 均半正定,即
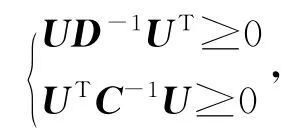
且当仅当U=0时上式等号成立。故
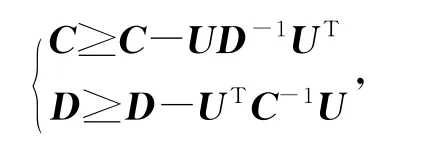
进而得

因此

且当仅当U=0时上式等号成立,证毕。
U=0要求条件

同时成立,故求解GDOP最小值的问题转化为寻找满足上述条件的(exi,eyi,ezi),i=1,2,…,n.获得方程(13)的解析解比较困难,根据上述条件和卫星在空间分布越分散GDOP值越小的要求,当n=4时,可构造一族解如下所示:

经过分析可以发现,这一组解不但满足上述条件式(13),而且满足故此时矩阵为C对角矩阵。这一族解有明确的几何意义:接收机与4颗卫星组成一个对称的六面锥,中心与Z轴重合,接收机在锥尖位置,4颗卫星不在与XOY平行的平面上,这个六面锥投影在XOY平面上是一个菱形。如果α=β,则4颗卫星在与XOY平行的平面上,接收机与4颗卫星组成一个以正方形为底的五面锥,但此时系数矩阵H奇异,这样的解不可取。
将这一族解代入到矩阵HTH中,得到GDOP最小值的计算公式为
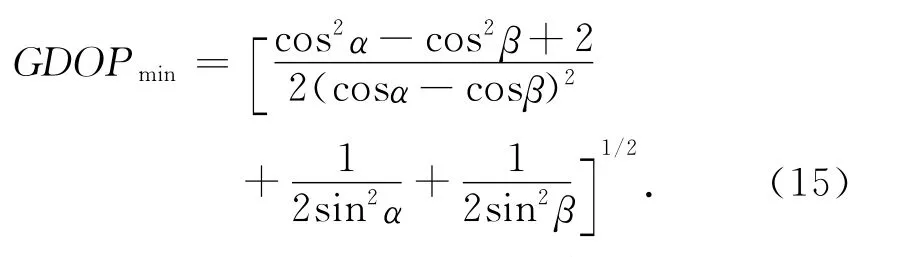
根据上式可以方便地利用数值法得到GDOP的最小值。
当n=5时,可构造一族解为
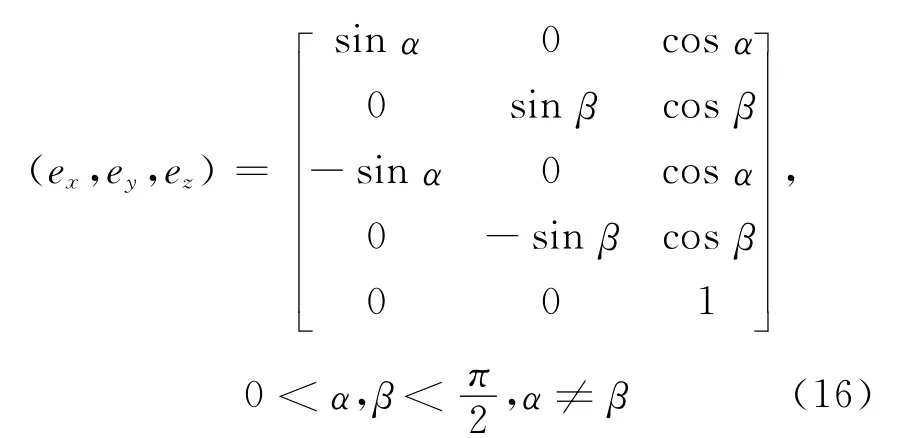
相应地,GDOP最小值的计算公式为

此时在n=4的基础上,增加的第5颗卫星在接收机正上方,即位于Z轴正上方的位置,此时GDOP值亦达到最小。
3 仿真与分析
算例1:为了验证本文推导出的GDOP理论最小值的正确性,以4颗、5颗可视卫星为例进行仿真分析。分别按下列三种方案计算相应的GDOP最小值,计算结果如表1所示。
1)用该方法计算得到GDOP的最小值,记为GDOPmin1.
3)根据美国JPL喷气动力实验室网站提供的卫星轨道根数等数据,不考虑各种误差的影响,采用外推法计算GDOP的最小值。这个GDOP最小值应该是相对真实的,记为GDOPtrue.

表1 三种方案得到的GDOP最小值
算例2:为了进一步验证本文结果的正确性,利用XW-GPS1000接收机在郑州市区采集一天的GPS静态数据,采样周期为1s,分析处理后可以得到GDOP值随可视卫星数变化的曲线如图1所示。

图1 卫星GDOP值变化曲线
由图1可以看出,对于GPS卫星导航系统,由于受卫星数目和卫星轨道长时间变化的限制及观测时卫星高度截止角的影响,可视卫星数为4、5时,GDOP 最小值分别为3.492、2.430,比理论推导的GDOP最小值大的多。
4 结 论
对GNSS导航定位中GDOP最小值的计算方法进行了分析,得到了以下结论:
1)在导航定位中,接收机通常只能观测到卫星高度截止角大于0的卫星,因此相关文献给出的GDOP理论最小值是不合理的,也是不能达到的;
2)对GDOP最小值进行了重新分析和推导,得出当接收机在n颗卫星的空间几何分布满足一定条件时,GDOP达到最小值,并利用数值法得到了4颗、5颗可视卫星对应的GDOP最小值;
3)随着GNSS的发展,当多个卫星导航系统组合导航定位时,随着卫星数目的增加,卫星的空间几何分布会得到较大的改善,GDOP值将达到较小;
4)此研究成果可以为星座设计、导航定位精度分析等提供一定的理论参考。
[1]盛 琥,杨景曙,曾芳玲.伪距定位中的GDOP最小值[J].火力与指挥控制,2009,34(5):22-24.
[2]王泽民,伍 岳.GPS、Galileo及其组合导航定位的DOP值分析[J].武汉大学学报·信息科学版,2006,31(1):9-11.
[3]张育林,范 丽,张 艳,等.卫星星座理论与设计[M].北京:科学出版,2008.
[4]丛 丽,谈展中.卫星导航几何因子的分析与仿真[J].电子学报,2006,34(12).2204-2208.
[5]丛 丽,谈展中.提高卫星导航定位精度和实时性的选星算法[J].系统工程与电子技术,2008,30(10).1914-1917.
[6]YANG Yong,MIAO Lingjuan.GDOP results in allin-view positioning and in four optimum satellites positioning with GPS PRN codes ranging[C]//IEEE Position Location and Navigation Symposium,2004:723-727.
[7]SAIRO H,AIRO H,AKOPIAN D,et al.Weighted dilution of precision as quality measure in satellite positioning[J].IEEE Radar,Sonar and Navigation,2003,150(6):430-436.
[8]李建文,李作虎,周 巍,等.卫星导航中几何精度衰减因子最小值分析及应用[J].测绘学报,2011,40(增刊),85-89.
[9]何晓峰.北斗/微惯性组合导航方法研究[D].长沙:国防科学技术大学,2009.
[10]谭述森.卫星导航定位工程[M].北京:国防工业出版社,2007.

