径向基函数神经网络在卫星钟差预报中的应用＊

雷 雨，赵丹宁

（1．中国科学院国家授时中心，陕西 西安710600；2．中国科学院时间频率基准重点实验室，陕西 西安710600；3．中国科学院精密导航定位与定时技术重点实验室，陕西 西安710600；4．中国科学院，北京100049）

0 引 言

卫星钟差的精度直接影响着全球卫星导航系统（GNSS）的导航定位结果，主要体现在以下两个方面:首先，卫星钟差参数通过导航电文发播，任意时刻的钟差是通过外推得到的，其预报精度直接决定了导航定位的精度［1］；其次，在实时精密单点定位（PPP）中，为了达到厘米级的定位精度，需采用预报钟差参与解算［2］。因此，提高卫星钟差的预报精度具有重要意义。

较常用的钟差预报模型为多项式模型和灰色模型，许多学者对其进行了研究，并取得了显著的效果［3－4］。但这两种模型都存在一定的局限性:多项式模型的预报精度会随着预报时间的延长而降低［4］，此外，该方法易受多项式拟合阶数等人为因素的影响；而灰色模型对钟差数据类型有较强的依赖性，要求钟差数据平滑且呈指数规律变化，限制了其应用范围［5］。近年来，国内外学者又发展了多种钟差预报模型［6－7］，其中神经网络（NN）由于具有通过学习训练以任意精度逼近任意连续函数的能力，在钟差预报中取得了良好的效果［8－10］。李孝辉等首次将误差反向传播（BP）神经网络应用于原子钟钟差预报中，研究表明神经网络比AR模型的预报精度高，且钟差异常值对BP神经网络模型预报性能的影响较小；郭承军等将径向基函数（RBF）神经网络应用于卫星钟差预报中，研究表明:神经网络比灰色模型具有更好的预报精度和稳定性；王威等采用RBF神经网络的变型—广义回归神经网络（GRNN）对卫星钟差进行建模并预报，从输入维数。光滑因子等几个方面对预报性能的影响进行了较为系统的研究，结果表明GRNN预报模型优于传统的二次多项式模型。应用RBF神经网络进行卫星钟差预报，由于神经网络易学习过度，从而影响网络的泛化（预报）能力，因而采用交叉验证法（CV）优化网络，并利用数值试验讨论了该方法的预报精度。

1 RBF神经网络

1985年，Powell提出了多变量插值的径向基函数方法。1988年，Moody和Darken提出了一种神经网络结构，即RBF神经网络，它能够以任意精度逼近任意连续函数，与BP神经网络相比，RBF神经网络具有学习速度快、全局收敛等优点。

1．1 RBF神经网络的结构

RBF神经网络是一种三层前馈式神经网络，包括一个输入层、一个隐含层和一个输出层。输入层由信号源结点组成；第二层为隐含层，隐含层神经元数目视所描述问题的需要而定，隐含层神经元的传递函数是对中心点径向对称且衰减的非负非线性函数；第三层为输出层，它对输入模式的作用做出响应。从输入空间到隐含层空间的变换是非线性的，而从隐含层空间到输出层空间的变换是线性的。

RBF网络的基本思想是:以径向基函数作为隐含层神经元的基构成隐含层空间，这样就可以将输入矢量直接映射到隐含层空间，而不像BP网络那样需要权连接，当RBF的中心点确定以后，这种映射关系也就确定了。而隐含层空间到输出空间的映射是线性的，即网络的输出是隐含层神经元输出的线性加权和，此处的权即为网络可调参数。由此可见，从总体上看，网络由输入到输出的映射是非线性的，而网络输出对可调参数而言却又是线性的。这样网络的权就可以由线性方程直接解出，从而大大加快学习速度并避免局部极小问题。

RBF网络的关键在于隐含层节点径向基函数的非线性逼近性能，径向基函数表现为多种形式，常见的为高斯函数，其形式如下:

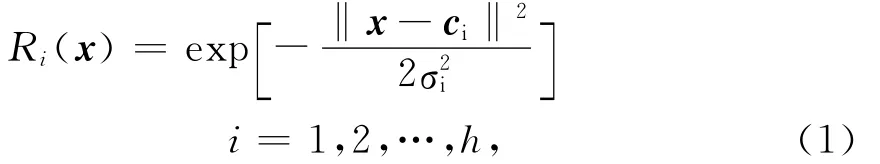
式中:x为输入向量；ci为隐含层第i个节点的中心向量，与x同维；σi表示高斯函数的宽度；‖xci‖为向量x－ci的欧式范数；h表示隐含层神经元的个数。

输出层节点相应的输出可表示为

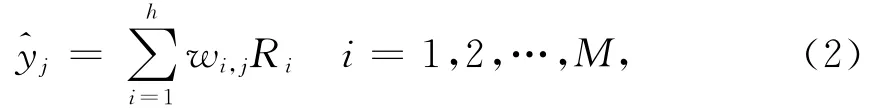
式中:＾yj为第j个输出单元的输出值；M表示输出层神经元的个数；wi，j为第i个隐单元到第j个输出单元的权值。

1．2 RBF神经网络的学习算法

通常，RBF网络的学习分为2个阶段进行，即隐含层的学习和输出层的学习2步。

1）隐含层学习

隐含层学习表现在隐含层神经元的数目h、中心向量c和高斯函数的宽度σ的确定上。其中，隐含层神经元数目的确定是关键问题，传统的做法是使其与训练集样本数目相同；而中心可根据训练样本点在自变量空间的分布，选出或计算出有“代表性“的点作为中心点，再由中心周围的样本点确定宽度σ，应用较多的为聚类分析法。

2）输出层学习

输出层学习体现在隐含层与输出层间的连接权w的确定上，可以应用最小二乘法对网络输出权值进行训练，其学习训练的目标是使总误差达到最小。

1．3 RBF神经网络的MATLAB工具箱函数

1）RBF神经网络创建函数

MATLAB函数newrbe用于创建一个精确的RBF神经网络，其调用格式如下:

net＝newrbe（P，T，spread），

其中，P为网络的输入向量；T为网络目标向量（输出向量）；spread为径向基函数的宽度σ（默认为1．0）；net为创建好的RBF网络。

在MATLAB中，没有专门的RBF神经网络训练和学习函数，这是因为在使用函数newrbe创建RBF网络的过程中，newrbe函数就根据训练样本P、T确定了网络结构，即隐含层神经元数、权值和阈值等网络参数。函数newrbe需要调节的参数只有一个spread，一般根据先验知识选取。newrbe函数创建网络的过程为

①隐层神经元数目等于输入样本数，其权值等于输入向量的转置:

式中:IW为隐层神经元的权值；PT为输入向量P的转置。

②设置隐层神经元的阈值为b

③以隐含层神经元的输出作为输出层神经元的输入，确定输出层神经元的权值和阈值，使之满足:

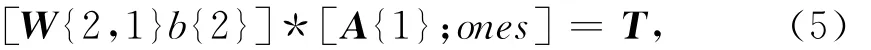
式中:W｛2，1｝、b｛2｝分别为输出层神经元的权值和阈值；A｛1｝为隐含层神经元的输出。

可以看出，上述过程只要进行一次就可以得到一个零误差的径向基网络，所以以newrbe函数创建网络的速度是比较快的，但由于隐层神经元数等于输入样本数，如果输入向量数目很大时，将导致网络的规模也很大。

2）RBF神经网络仿真函数

函数sim用于利用已经创建好的RBF神经网络进行仿真预测，其调用格式为

＾y＝sim（net，＾P），

其中，net为创建好的RBF网络；＾P为网络的输入向量；＾y为网络输出向量。

2 交叉验证法

神经网络对训练样本的逼近称为拟合，而对非训练样本的逼近称为泛化（预报）。显然，衡量一个网络训练好坏的标准不仅是要考察网络的拟合能力，更要检验其泛化能力，即训练神经网络的最终目的是确保训练好的网络同时具有良好的拟合能力及泛化能力。一般情况下，训练能力差时网络的泛化能力也弱，并且在一定程度上随着训练能力的提高泛化能力也会随之提高，但是这种趋势有一个极限，达到此极限后，随着训练能力的提高，泛化能力反而下降，即出现所谓过适性或过拟合，也称为过学习，此时网络学习了过多的样本细节而不能反映样本所蕴含的内在规律。欠学习。过学习的网络都属于不成熟网络，泛化能力会很差，实际中网络往往是过拟合。从上述意义上讲，网络训练过程中存在两方面的问题:

1）神经网络对训练样本有较强的依赖性，如何从有限的训练样本中挖掘更多的信息是网络训练好坏的关键；

2）在网络训练过程中要着重考察网络的泛化能力，避免发生网络过学习的状态。

解决上述问题的一个有效方法是采用交叉验证法优化网络。交叉验证法的基本思想是在某种意义下将学习集进行分组，一部分做为训练集，另一部分做为验证集，首先用训练集对神经网络进行训练，再利用验证集来测试训练得到的模型，以此来做为评价网络性能的指标。交叉验证法的一种改进方法是 K 重交叉验证法（K－fold Cross－Validation）［11］，其工作方式如下:假定有个 N 样本，将其随机均匀分成K份，轮流选择其中K－1份作为训练样本对网络进行训练，剩余的1份作为验证（其样本个数为N／K）校本以检验网络的泛化性能。网络需要训练K次，也就可以创建K个网络，选择泛化误差最小时的网络模型为最优模型，用均方根误差（RMSE）来衡量泛化误差:

式中:RMSE（j）表示第j次训练的网络泛化误差；j＝1，2，…，K；yi为理论值；＾yi为网络输出值。

3 基于RBF神经网络的钟差预报

3．1 利用RBF神经网络进行钟差预报的过程

利用RBF神经网络方法进行钟差预报的过程为:

1）确定网络的输入，输出量及相应的维数。输入量为已知的钟差值，输出量为钟差预报值。

2）根据已知数据，进行学习集与测试集的分配。

3）数据的归一化，由于各历元钟差数据相差悬殊，即输入变量差异较大，为了使网络训练一开始就给各输入分量以同等重要的地位，需要将输入数据变换到同一范围中。选用由MATLAB提供的premnmx函数，将输入数据和与之对应的输出数据进行归一化处理，使处理后数据全部落在（－1，1）的范围内，这样有利于提高神经网络的收敛速度，节省网络训练耗时，并且可以防止发生突变的钟差数据对网络训练的影响。

premnmx函数的模型为

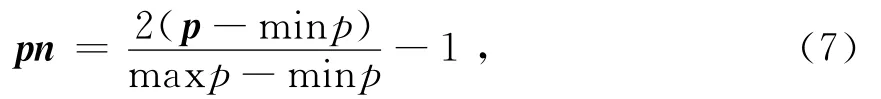
式中:p为需要归一化的数据；pn为归一化后的数据；minp、maxp分别表示p中的最大值和最小值。

4）网络创建和训练。采用MATLAB神经网络工具箱函数newrbe建立RBF神经网络，并根据学习集采用K重交叉验证法优化网络模型。

5）网络仿真测试。利用训练好的RBF神经网络进行钟差预报。

6）预报结果的逆归一化处理，并对还原结果进行检验。

3．2 试验结果与分析

为了分析RBF神经网络模型预报卫星钟差的精度，选取3颗钟差变化较典型的卫星，分别是PRN03、PRN05和PRN08，其中PRN03呈递增变化，PRN05呈递减变化，而PRN08既呈递增也呈递减变化，具体的钟差变化如图4～6所示。采用的数据为2010年11月28日至30日的IGS事后GPS精密钟差，采样间隔为5min．由于灰色模型的钟差预报效果优于二次多项式模型［3］，为了验证RBF网络的效果，采用灰色模型GM（1，1）对卫星钟差预报，并将两者加以比较。其中，3．2．1节给出了基于交叉验证法的网络训练结果；3．2．2节将传统灰色系统模型与RBF神经网络模型的预报精度进行对比分析。

3．2．1 交叉验证法试验分析

算例中将28日和29日2天的数据作为学习集用于RBF神经网络的学习训练，将30日的数据作为测试集以检验模型效果，采用4重交叉验证法将学习样本随机分成4份，其中3份作为训练样本，剩余1份作为验证样本，由于是用MATLAB函数newrbe实现RBF神经网络的钟差建模，因此每次训练时需要调节的参数只一个spread，即径向基函数的宽度σ，在（0．1，5）的范围内选取，步长取0．1，对于每次训练，验证误差（泛化误差）最小时所对应的值即为最优值。只给出PRN08卫星的钟差在训练过程中训练误差（拟合误差）和验证误差的变化情况，如图1所示，其中横坐标代表径向基函数的宽度σ（spread），纵坐标代表均方根误差（RMSE）。

由图1可以看出，每次训练的结果是训练误差几乎相同，都不超过1ps，但验证误差却不尽相同，这说明网络的拟合能力与其泛化能力在某种程度上并没有必然的联系。为了更好、更直观的反映网络训练效果，将图1中的验证误差图（图1b）的部分区域放大作图，放大后如图2（a）、图2（b）所示。另外，表1给出了每次训练的最小验证误差。

结合图1、2，分析表1，可以更清楚地看出:

1）spread对网络性能有重要的影响。实际应用中，对于特定的卫星钟差数据，spread值的调节过程有一定的规律，对于PRN08卫星钟差数据，在一定的范围内，spread值越大网络性能越好，另外，每次训练得到的最优spread值并不相同；

2）随着训练次数的增加，拟合误差几乎没有变化，而验证误差则是先减小后增大，存在最小点，对应的最小值为0．211 4ns，出现在第2次训练过程中，对应的拟合误差和spread值分别为0．62 ps、2．4；

3）交叉验证法通过多次训练网络能够优化网络模型，比只训练一次的泛化误差更小。

表1 验证误差／ns

为了验证交叉验证法的有效性，突出其优点，将其同常规方法（将学习样本全部用来训练网络）进行对比，图3示出了两种方法对同一测试样本的测试误差。对于常规方法，测试误差RMSE为17．30ns，而对于交叉验证法，测试误差RMSE仅为6．03ns，显然，交叉验证法可以明显提高网络的泛化能力。

图3 两种方法的测试误差

3．2．2 灰色系统模型与RBF神经网络模型预报精度对比分析

分别利用灰色系统模型GM（1，1）和基于交叉验证法的RBF神经网络模型对3颗卫星的钟差作24h的短期预报并进行误差比较，如图4～6所示。

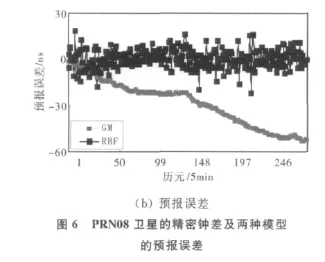
由图4～6可以看出，传统灰色模型对不同卫星钟差在短期预报误差异常波动很大，对钟差数据类型有较强的依赖性，因此对于卫星钟差短期预报而言，RBF神经网络模型的预报精度和稳定性要明显优于传统灰色模型，可以在实际应用中来代替灰色模型。

为了进一步研究RBF神经网络模型在卫星钟差短期预报中的性能，对上述预报结果作误差统计特性分析，如表2所示，其中MAX代表最大误差，MEAN代表平均误差，STD代表标准差。

表2 预报误差统计／ns

由表2可以更清楚地看出，对于卫星钟差短期预报来讲，RBF神经网络模型较传统灰色模型有更高的预报精度和更好的稳定性，然而RBF神经网络模型也有一定的局限性，主要是对训练样本有一定的要求，体现在以下2个方面:

1）对训练样本的数量有一定要求，如果训练样本过少，网络的学习效果就不是很好，相应地就会影响网络的泛化能力，但训练样本也不能太多，过多的样本将会导致过长的网络训练耗时；

2）要求训练样本数据具有一定的代表性，即能够表征系统的变化特性，否则网络的泛化能力也就不强。

4 结 论

通过以上对RBF神经网络在卫星钟差预报中的分析可以看出，RBF神经网络模型较传统的灰色系统模型在钟差预报方面有一定的优势，模型精度和稳定性均有所提高。在MATLAB环境下对RBF神经网络建模，对参数要求较低，需要调节的只有一个径向基函数的宽度参数，容易实现。但模型本身也有一定的局限性，对样本数据依赖性强，且容易学习过度，对于后者，可采用交叉验证法训练网络避免，试验也表明该方法可以明显提高网络的泛化能力。另外，模型只适用于短期预报，如果要用于长期预报，则需要不断增加新的样本数据对模型进行再训练。

仅仅对RBF神经网络在卫星钟差预报中应用的初步研究，所用方法尚需改进和完善，如何对模型进行优化以提高预报精度，以及如何将模型用于长期预报是下一步的研究重点。

［1］ 吴海涛，李孝辉，卢晓春，等．卫星导航系统时间基础［M］．北京:科学出版社，2011．

［2］ 李 黎，匡翠林，朱建军．基于IGU预报轨道实时估计精密卫星钟差［J］．大地测量与地球动力学，2011，31（2）:111－116．

［3］ 崔先强，焦文海．灰色系统模型在卫星钟差预报中的应用［J］．武汉大学学报·信息科学版，2005，30（5）:447－450．

［4］ 郑作亚，卢秀山．几种GPS卫星钟差预报方法比较及精度分析［J］．山东科技大学·自然科学版，2008，27（4）:6－11，15．

［5］ 朱陵凤，吴晓平，李 超，等．灰色模型在卫星钟差预报钟的缺陷分析［J］．宇航计测技术，2007，27（4）:34，42－44．

［6］ 朱祥维，肖 华，雍少为，等．卫星钟差预报的Kalman算法及其性能分析［J］．宇航学报，2008，29（3）:966－970，1052．

［7］ 黄观文，张 勤，许国昌．基于频谱分析的IGS精密星历卫星钟差精度分析研究［J］．武汉大学学报·信息科学版，2008，33（5）:496－499．

［8］ 李孝辉，柯熙政．原子钟信号的神经网络模型［J］．陕西天文台台刊，2001，23（2）:110－115．

［9］ 郭承军，滕云龙．基于小波分析和神经网络的卫星钟差预报性能分析［J］．天文学报，2010，51（4）:395－403．

［10］ 王 威，荣志飞，范国清．基于GRNN的导航卫星钟差仿真方法研究［J］．系统仿真学报，2011，23（11）:2339－2345．

［11］ 丁常富，王 亮．基于交叉验证法的BP神经网络在汽轮机故障诊断中的应用［J］．电力科学与工程，2008，24（3）:31－34．