地基GPS倾斜路径水汽计算方法研究*
朱 爽
(中国地震局第一监测中心,天津300180)
0 引 言
地基GPS水汽探测技术可以利用GPS观测数据计算出高精度的可降水汽量PWV,精度可以达到1~2mm[1].但PWV是指测站上空天顶方向上总的水汽含量,它所反映的是测站上空一段时间内所有GPS传播路径上的一维平均水汽,并不能提供水汽的三维分布信息,这在某种程度上影响了地基GPS在数值天气预报上的应用[1]。Davis等人(1993)研究发现:当站点上空30°仰角时,利用微波辐射计观测得到的水汽分布信息在不同方位上会有20%的变化[2]。一维的PWV是不能给出水汽的这种空间变化的,这促进了GPS信号斜路径方向上的水汽总量(SWV)的发展。Ware等人[3]首先开始了应用GPS观测斜路径延迟STD的研究工作,利用双差法证明了GPS观测斜路径延迟STD 的可行性[3];Alber等人 提出了一种从双差残差中获得信号路径上相位延迟的方法[4],加快了这方面的研究进展;宋淑丽等人使用了一种直接计算SWV的方法[5],认为其观测精度在mm量级。SWV在气象领域的应用研究也相继开展,研究证实,把SWV同化到数值天气预报模式的初始场中,即可以重构水汽的三维分布场,这对数值天气预报具有重要的意义[6]。MacDonald利用3D VAR方法从SWV观测值中获得了水汽的三维分布,并进行与中尺度天气数值模式水汽场的对比分析[7],实验证明较高分辨率的GPS接收机可以进行水气的三维层析。
介绍了利用GPS进行倾斜路径水汽含量计算的方法,同时介绍了利用微波辐射计WVR计算倾斜路径水汽含量的原理,在此基础之上,利用GPS与微波辐射计WVR的并址观测站2002年5月26日的观测数据进行实验,将实验结果进行对比。对比结果显示,利用地基GPS可以实现倾斜路径上可降水汽量(SWV)的计算,其与WVR观测值的偏差平均值为1.83mm,均方根误差为4.23mm.实验同时证明:倾斜路径水汽含量与卫星高度角有很强的关系,高度角较低时,误差较大,高度角较低时,误差较小。
1 倾斜路径水汽含量的计算方法
在高精度GPS数据处理中,通常把对流层延迟表示为天顶方向的延迟量ZTD与高度角有关的映射函数M(E)之积,而天顶方向的总延迟量(ZTD)分为天顶干延迟 (ZHD)和天顶湿延迟(ZWD)之和,且对于天顶干延迟和天顶湿延迟采用不同的映射函数,为
ΔDtrop=ZTD·M(E)
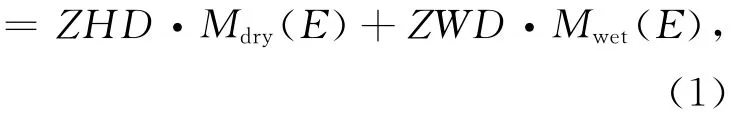
式中,Mdry(E)和Mwet(E)分别为天顶干、湿延迟的映射函数。
获得天顶湿延迟后,即可由式(2)得出天顶方向可降水汽量

其中,∏为无量纲水汽转换系数,它的表达式为
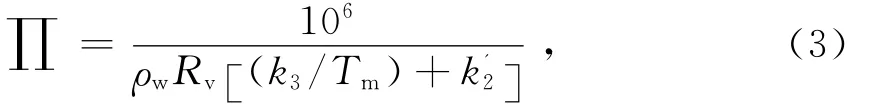
式中:Rv为气体常数;k'2和k3分别为大气折射常数;Tm为大气加权平均温度。
而当GPS卫星信号在经过对流层大气时,信号是沿着倾斜路径进行传播的。倾斜路径方向上的湿延迟为接收机至卫星之间湿折射率的积分[4]。
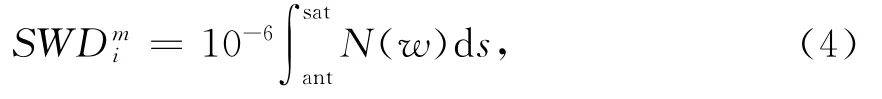
式中:SWDmi为倾斜路径上测站i与卫星m 之间的湿延迟;ant代表 GPS接收机天线;sat代表GPS卫星;s代表积分信号路径,湿折射率N(w)为水汽分压ew及温度T的函数 :

式中,常数k=3.73×105K2hpa-1.
倾斜路径上的水汽总量SWV可由式(6)计算所得

式中,∏为前述计算PWV时所使用的无量纲比例因子。
一个SWD观测值可以看作是两部分之和,一个部分是各向同性部分,即天顶湿延迟量ZWD,它可以认为是一段观测时间内一个测站到所有可见卫星的SWD观测值映射到天顶方向后的平均值,天顶方向水汽含量PWV意味着水汽在一段时间内保持不变且是水平均匀的,但实际上这种情况并不总是正确的,在发生强对流、台风等天气时,水汽场的空间变化十分复杂,显然PWV不能给出这种空间变化信息。第二个部分是各向异性部分,即斜路径延迟对各向同性成分ZWD的偏离,这一项即是不同方位角上的差异[8-9]。
由上分析可知,斜路径延迟水量SWV由各向同性部分PWV和各向异性部分组成。PWV代表了大气在天顶方向上的平均值,各向异性可以认为是SWV在天顶方向上的偏离。其中,各向异性成分又包括了水平梯度项和观测值相位残差两项。基于以上分析,可以得出STD的计算公式:

式中:e为卫星高度角;φ为卫星方位角;Mdry(e)为干映射函数;Mwet(e)为湿映射函数;MΔ(e)为水平梯度映射函数;GNS为南北方向的水平梯度,GWE为东西方向的水平梯度;Re为倾斜路径的相位残差。在GAMIT中,
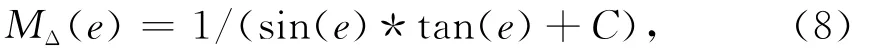
式中,C=0.003 2.
则SWV的计算公式:
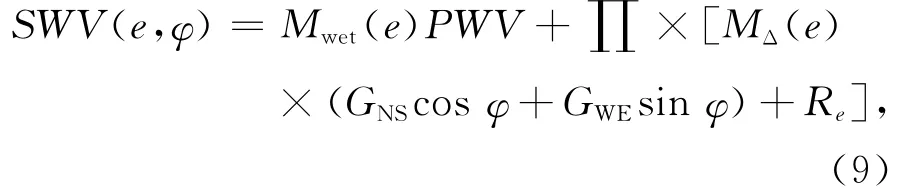
在高精度GPS数据处理中,常采用的计算对流层参数的方法有非差精密单点定位法(PPP)和双差法,在有远距离测站参与解算时,PPP和双差法的精度相当。基于PPP的方法具有估计模型简单、无需引入远距离参考站、实时快速的特点,美国的GIPSY和德国的EPOS软件都是基于PPP进行参数估计。但是,基于精密单点定位时,高精度钟差的获取使得它较难获得高精度的估计结果。而在双差法中,接收机钟差及卫星钟差都通过双差法消除,并且可以准确地获得整周模糊度,GAMIT软件和瑞士伯尔尼大学的BERNESE软件都采用双差法进行参数估计。以GAMIT为基础进行斜路径延迟的估算。
2 微波辐射计WVR计算SWV的原理
WVR微波辐射计是观测大气信息的一种仪器,它可以借助微波辐射传输方程观测天空亮温,从而反演倾斜路径上的湿延迟量SWD和水汽总量SWV.它可连续跟踪单颗GPS卫星,大约5~10min完成一组观测。WVR可以探测天空的辐射,然后输出天空亮温,正比于天空亮温的数字信号及观测方向上的光学厚度。其传输方程为
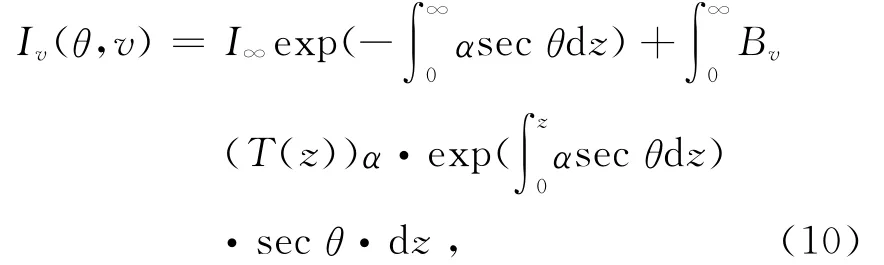
式中:I∞为宇宙背景的微波辐射强度;θ为天顶角;v为频度;T(z)为温度廓线;Bv(T(z))为黑体辐射强度;α为吸收系数,由水汽分子、云中液水和氧气分子吸收系数三项构成。式(10)即为大气中微波传输的基本方程。
通常情况下,选用不同的两个通道频率,一般为22.2GHz和35.3GHz,从地面和探空数据可以计算地面接收到的辐射,对应每一个探空曲线,可以得到两个波段上的不同亮温。结合亮温、平方项、地面气压、湿度等,进行逐步回归,即可以得到水汽总量L的反演方程为

式中:A,B,C为回归系数,根据不同地点的具体情况设定;θ为天顶角。
WVR观测得到的延迟信息精度较高,可以达到5mm,通常作为GPS斜路径水汽信息的对照信息。需要注意的是,在大气水汽含量较高或者正在降雨时,WVR的观测结果是不可靠的。所选择WVR观测所得的延迟信息进行对比,用来检验GPS斜路径水汽计算的正确性。
3 倾斜路径水汽SWV的解算结果验证
3.1 数据说明
选用了卡尔加里大学提供的GPS、微波辐射计WVR的并址站uofc站2002年5月26日(年积日第146天)的数据进行实验。
利用GAMIT软件进行数据处理时,为了获取精度较高的水汽计算结果,加入了9个IGS观测站,分别为 ALGO,AMC2,DRAO,DUBO,FLIN,PIE1,PRDS,SHAO,YELL.
其中,GAMIT的解算策略如下:星历采用广播星历,截止高度角为10°,基线处理模式为RELAX(松驰解),电离层延迟模型为LC-HELP,对流层模型为Saastamoinen模型,映射函数为NMF模型,测站坐标约束为0.010m,每1h估计一次对流层参数。
3.2 验证结果分析
利用GAMIT计算得到的天顶方向水汽量PWV与WVR提供的结果进行对比。由于WVR提供的值为每个时刻对单颗卫星的观测结果,因此将10min内的所有观测值取平均,得到每隔10 min的天顶可降水汽量。另外,GAMIT得到的原始结果是每1h获取一个PWV,将间隔为1h的数据内插为每隔10min一次的数据进行对比。图1示出了对比结果。

图1 利用GPS与WVR得到的PWV对比图
由图1可以看出,通过GPS数据解算的PWV结果与WVR提供的结果变化趋势一致,误差较小。在此基础之上,对两者的结果进行了统计分析,偏差的平均值为1.17mm,均方根误差为1.75 mm.本结果与国际上PWV的计算误差1~2mm的精度相当,也为后续的SWV对比提供了可靠的PWV值。
选取了第146日UOFC站上25、21、14、18号卫星的GPS、WVR观测结果进行对比,由于WVR对单颗卫星的观测时间间隔约为8min,而GPS对单颗卫星的观测时间间隔为30min,按照WVR的观测时刻选取了GPS相应观测时刻的值来进行对比。结果如图2所示。

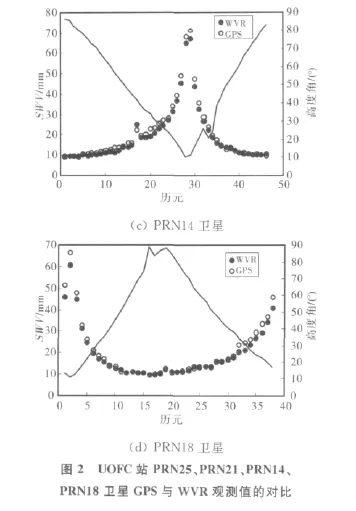
由图2可明显看出,随着高度角的降低,GPS与WVR获得的SWV都逐渐增大,两者的变化趋势一致。在高度角较高时,两者的值都较小,这时因为高度角较高,倾斜路径几乎等于垂直路径,斜路径延迟中的各向异性部分较小,SWV与PWV的值相近;高度角降低,SWV逐渐增大,这是因为高度角较低,斜路径与垂直路径偏差较大,各向异性部分增大,导致SWV与PWV的偏差较大。另外,将基于GPS与WVR的SWV偏差进行对比,如图3所示。
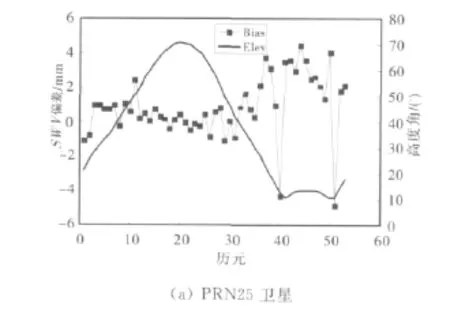

由图3可以看出,高度角较高时,两者的误差较小,一般在-1与1mm之间;高度角变低时,两者的误差较大,高达6mm.这是因为在高度角较低时,SWV的各向异性成分变大,估计过程中由于非差残差和多路径效应及其它非模型化的误差难以准确得到,导致低高度角时SWV的估计误差变大。
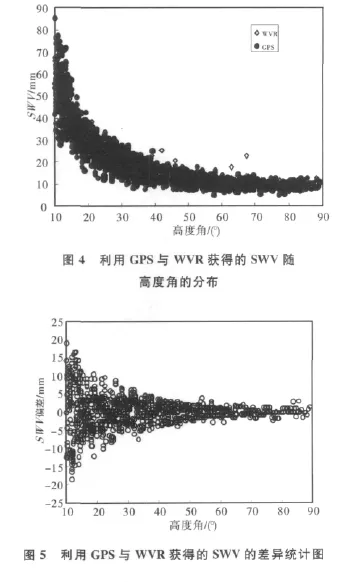
图4是UOFC站第146日所有观测时刻GPS与WVR所得的SWV随高度角的分布图。图5是两者的差值统计图。
由图4、5可以明显看出,随着高度角的增大,SWV的值逐渐减小,这与图2的情况相符合;同时,随着高度角的增大,利用GPS与WVR获得的SWV差值也逐渐减小,这与图3情况相符合。同时也证明了前文中的分析是正确的。统计了该天所有观测数据的差值,差值平均值为1.83mm,均方根误差为4.23mm.综合以上分析可以得知,利用GPS观测数据,采用双差法可以计算出精度较高的SWV.
值得一提的是,当高度角较低时,GPS与SWV的误差较大,这是由于在低高度角时,SWV的各向异性成分较大,利用GPS估计各向异性成分的过程中产生较大误差。在数据处理中,要先确定PWV准确的获得,在此基础之上,进行各向异性成分的计算;在计算过程中,要减少多路径效应的影响,同时,可以改进在非差残差获得过程中的定权方式,比如采用根据高度角定权,另外还要考虑残余的未模型化的大气延迟。由于数据有限,还需进行更深入的研究。
4 结 论
一维的PWV是天顶方向上的水汽含量,不能全面反映水汽的分布信息,而SWV是倾斜路径上的水汽含量,它包括各向同性部分,即天顶方向上的PWV,以及各向异性部分。由于SWV可以反映水汽在不同方位上的分布,对于研究水汽的三维层析及时空变化具有重要意义。利用GPS观测数据获得了倾斜路径上的SWV,并与WVR提供的数据进行对比,结果表明,两者的差值平均值为1.83mm,均方根误差为4.23mm.实验分析还得出,倾斜路径上的SWV与高度角存在很大的相关性,高度角较低时,SWV的值明显增大,这是由于低高度角时SWV的各向异性成分明显增大;而高底角较高时,SWV的值与PWV的值相差不大,估计精度也较高。
[1] 毕研盟.应用全球定位系统(GPS)遥感大气水汽的研究[D].北京:北京大学,2006.
[2] DEVIS J,ELGERED G,NIELL A,et al.Groundbased measurement of gradients in the"wet"radio refractivity of air[J].Radio Sci.1993,28(6):1003-1018.
[3] WARE R,ALBER C,ROCKEN C,et al.Sensing integrated water vapor along GPS ray paths.Geophys[J].Res.Lett.,1997(24):417-420.
[4] ALBER C,WARE R,ROCKEN C,et al.Obtaining single path phase delays from GPS double differences.Geophys[J].Res.Lett.,2000(27):2661-2664.
[5] 宋淑丽,朱文耀,程宗颐,等.GPS信号斜路径方向水汽含量的计算方法[J].天文学报,2004,45(3),338-346.
[6] GUO Y R,KUO Y H,DUDHIA J,et al.Four-dimensional variational data assimilation of heterogeneous mesosacle observations for a strong convective case.[J].Mon.Wea Rev,2000(128):619-643.
[7] MACDONALD A E.XIE Yuanfu,WARE R H.Diagnosis of three-dimensional water vapor using slant observations from a GPS network[J].Mon.Wea Rev.2002,130 (2),386-397.
[8] 宋淑丽.地基GPS网对水汽三维分布的监测及其在气象学中的应用[D].上海:中国科学院研究生院,2004.
[9] 张双成.地基GPS遥感水汽空间分布技术及其应用的研究[D].武汉:武汉大学,2009.
——环地平弧&环天顶弧

