软岩隧道掌子面挤出与拱顶沉降变形相关性

朱得华，梁 斌，李治国

(1.河南科技大学规划与建筑工程学院，河南洛阳471023;2.中铁隧道集团有限公司，河南洛阳471009)

0 引言

隧道开挖介质相对于隧道开挖行为的变形反应是每名隧道设计人员必须关注的首要问题，这是因为与其他因素相比，隧道开挖介质相对于隧道开挖行为的变形反应预示着是否能够引发成拱效应以及成拱效应的位置，换句话讲，也决定了隧道所能达到的稳定等级。通过研究发现:变形反应从掌子面前方的超前核心土开始，随之逐步沿隧道向后发展;而且变形不仅包括收敛变形，而是由挤出变形、预收敛及收敛变形组成。隧道掌子面和超前核心土体系的变形反应与隧道变形之间有直接联系，而且前者是因后者是果。从而强调监控掌子面～超前核心土体系变形反应的重要性，而不是只监控隧道自身的变形，对于这方面的研究，国外已经取得了一定的成果[1-5］。针对隧道变形方面，国内也有一些相关研究。文献[6］研究了长大隧道软弱围岩段施工大变形的预测方法，运用BP神经网络和遗传算法进行长大隧道软岩段施工大变形预测;文献[7-9］通过隧道收敛和围岩内部位移的现场监测、理论分析，对隧道的变形进行了系统研究。新意法把超前核心土视作一种新的隧道长期和短期稳定工具:超前核心土的强度及对变形的敏感性在隧道施工中起决定性作用，同时也决定了掌子面到达时隧道的变形特性。

掌子面挤出变形是开挖介质对隧道开挖产生的变形反应的主要表现形式，主要发生在超前核心土内;挤出变形的大小取决于超前核心土的强度、变形特性及其所处的原始应力场;挤出变形发生在隧道掌子面的表面，沿隧道水平轴线方向发展，其几何形状大概呈轴对称(掌子面鼓出)，或在掌子面形成螺旋状突出[10-12］。

近年来为了能够大幅度提高隧道施工机械化的水平，使隧道施工安全、经济、快速高效，现在大断面隧道的施工逐步趋向于采用全断面法或全断面短台阶法。

本文依托于某软岩铁路隧道，该隧道采取了一定的超前预加固措施，实现了大断面施工，笔者主要研究了在施工期间，掌子面封闭后，施做跟进仰拱期间，考虑空间效应的围岩变形情况，并建立了数值计算模型，分析了施做仰拱期间掌子面挤出变形的变化规律，研究掌子面挤出变形与拱顶沉降变形之间联系，为以后类似工程的掌子面变形分析提供参考。

1 工程概况

1.1 工程水文地质

隧道穿行于黄河高阶地下部，主要涉及的地层为:第4系砂质黄土，风积砂质黄土，冲积卵石土，粗圆砾及细圆砾土。全隧道设计围岩为Ⅴ级。开挖揭示进出口及各斜井地层主要为粗细圆砾土、卵石土及遇水未成岩粉细砂，随后将隧道正洞未施工地段围岩级别调整为Ⅵ级。

目前，隧道出口掌子面为遇水粉细砂层，开挖后如不及时处理，涌砂、突水、溜塌现象频繁，该地区地下水为第4系孔隙水和基岩裂隙水。隧道洞身部分基岩裂隙水受补给源限制，其富水性较差。隧道洞身通过地段较为破碎，地下水不丰富。

1.2 施工方案

鉴于地层情况特殊，用传统CD、CRD等施工方案速度缓慢，施工风险不易控制。该隧道采用“水平旋喷超前加固(见图1)+大断面施工”施工方案，取得了不错的效果。主要通过隧道周边水平旋喷桩结合大管棚、掌子面水平旋喷结合玻璃纤维锚杆和隧道内部综合降水等措施对围岩进行预加固处理，采用挖掘机和破碎锤开挖，机械装运出渣。

图1 水平旋喷超前加固纵剖面示意图

2 测量方案

在每个施工循环开始，施做水平旋喷之前，需要封闭掌子面，把掌子面修整成60°～70°的坡，按1.5 m×1.5 m间距梅花形打设φ22 mm长2.5～3.0 m的锚杆，挂φ8 mm@20 cm×20 cm的钢筋网片，网片相互搭接，并与锚杆连接，然后喷20 cm厚的C25混凝土。

由于封闭掌子面到仰拱跟进到掌子面之间有1到2周的时间，在这期间掌子面地形会发生一定的变化，根据新意法的理论，掌子面核心土的这种变化会关系到隧道整个的稳定性，加上软弱地层的特殊性，在这期间在掌子面布置测点，对掌子面的变形变化进行观测(见图2)。

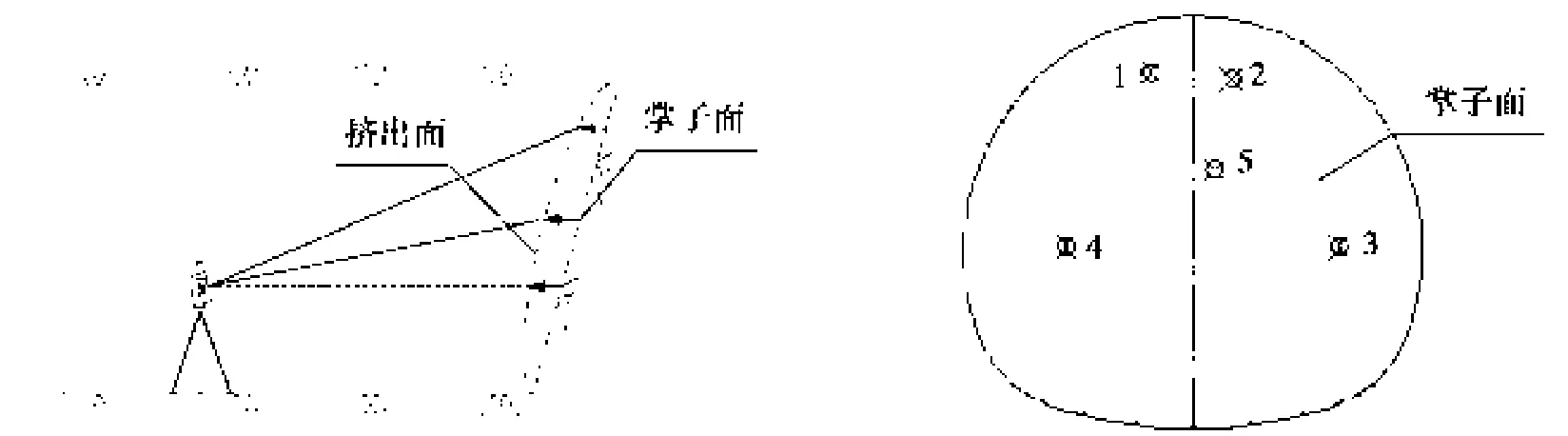
图2 掌子面挤出变形量测

测量方案:由于施工工序复杂，现场监测作业受到施工干扰问题突出，因此基于三维非接触测量原理，采用高精度全站仪进行量测[13］。在DK6+285掌子面布设发射膜片，反射膜片粘贴在掌子面露出锚杆的端部。测量时通过后方交汇采用绝对坐标进行测量，得到测点的三维坐标，通过投影换算，得到测点在隧道里程方向、隧道横向和高程的变化值，其中5个测点的初始位置见表1。掌子面后方每间隔5 m布设一个拱顶沉降测点，每天上、下午进行两次量测，分别采集了DK6+321～DK6+286共计8个监测断面的数据。

表1 测点的初始位置

3 测量结果分析

3.1 掌子面挤出变形分析

掌子面封闭后仰拱跟进期间，掌子面挤出变形曲线如图3所示，其中1号点～5号点的最大挤出变形分别为 19.3 mm、19.0 mm、10.8 mm、9.0 mm和15.5 mm。由图3可以看出:掌子面上高程越大的点挤出变形值越大，也就是说越靠近掌子面上方位置的挤出变形越大;随着仰拱施工靠近掌子面，掌子面挤出变形持续增大，分析曲线形状，发现变形曲线大致可以分为5个阶段:第1阶段:在3月22日～3月23日未进行仰拱开挖，曲线平稳，4号点出现很小幅度的减小;第2阶段:3月23日开挖仰拱，变化速率增大，在3月23日～3月26日开挖了5 m的仰拱，曲线平稳增长，变化速率保持一定;第3阶段:在3月26日～3月29日继续开挖了6 m仰拱，曲线平稳增长，变化速率一定;第4阶段:在3月29日处，变化速率继续增大，直至3月30日，在此期间开挖了8 m仰拱;第5阶段:在3月30日达到峰值，往后曲线呈线性减小;分析原因:30日至31日期间，仰拱开挖施工到DK6+295，由于离掌子面下台阶的距离较近(只有2 m左右)，施工开挖会引起掌子面发生向下的滑动，造成挤出变形值急剧减小。

图3 掌子面挤出变形曲线

表2为仰拱距掌子面距离与隧道半径的比例关系，由表2可以看出:仰拱施工过程和掌子面挤出变形有一定的相关性:仰拱施工距掌子面的距离L＞4R时，施工对掌子面挤出变形影响很小，可以忽略;仰拱施工距掌子面的距离2R＜L＜4R时，随着L的减小，掌子面挤出变形持续增大，在L≈3R处，累计变形速率发生变化，变化速率增大;仰拱施工距掌子面的距离L＜2R时，随着L的减小，累计变形呈减小趋势，下降速率快。

表2 仰拱里程与隧道半径的关系

3.2 拱顶沉降变形

为了分析掌子面挤出变形和拱顶沉降变形的相关性，选取了DK6+321～DK6+286共计8个监测断面的数据，其中，在3月22日以前，DK6+321和DK6+316两个断面的初支结构已经封闭。绘制曲线图时，为了方便分析，把3月22日的累计沉降统一记为0，以后每天的变形依次叠加。

图4为监测断面的拱顶沉降曲线，由图4可以看出:拱顶沉降曲线近似为线性变化;越靠近掌子面，在相同监测时间点，拱顶沉降量越大，则变形曲线的斜率越小，其中DK6+286除外。

经研究分析，DK6+286拱顶沉降反常有以下2个原因:

(1)该点的布设时间相对较晚，考虑到砂层的流变效应，拱顶的围岩与初支结构的协调变形没有充分的发展。

(2)该点距掌子面上台阶的距离仅有1 m左右，拱顶围岩与掌子面的核心土连通性好，掌子面的变形约束相对较小，应力释放的路径会偏向于掌子面，而拱顶位置的受力会相对减弱。

监测断面距掌子面距离S与拱顶沉降△的关系见表3。从表3中可以看出:当0＜S＜2R时，随着S值的增大拱顶沉降变形持续增大，但是速率较慢;当S＞2R时，随着S值增大，拱顶沉降变形继续增大，且变化速率增大。也就是说，临界的距离近似为2R，超出2R的范围，两者的相关度减弱。

根据3月22日至3月31日的监测数据，做出每个监测断面拱顶沉降与掌子面挤出变形数值的相关曲线，如图5所示。其中掌子面挤出变形值，取的是每天掌子面5个测点挤出变形的平均值，由于挤出变形曲线变化趋势相近，取平均值做出曲线有代表性。

图4 监测断面的拱顶沉降

图5 拱顶沉降与掌子面挤出变形的相关性曲线

表3 监测断面距掌子面距离与拱顶沉降的关系

4 数值模拟

4.1 计算模型与基本参数

4.1.1 计算模型

使用FLAC3D建立计算模型如图6所示，开挖跨度为15.62 m，开挖高度为13.68 m，隧道埋深为80 m。

4.1.2 边界条件

在垂直方向上限制模型底部的位移，在水平方向上限制模型两侧的位移，顶部承受上覆围岩的自重应力。

4.1.3 初始地应力场

主要考虑自重应力场，侧压力系数为0.9。

4.1.4 计算参数的选取

计算参数的选取见表4，其中，初支结构为c20喷射混凝土和I25a工字钢，拱架间距为0.5～0.7 m内外双层钢筋网，钢筋网为φ8钢筋，20 cm×20 cm，喷层厚度为33 cm;二衬为C45钢筋混凝土，厚度60 cm;仰拱充填混凝土为C25素混凝土。旋喷桩等效为厚度0.53 m的等厚度护壳。

图6 计算模型

表4 计算相关的参数

4.1.5 施工过程的模拟

开挖前先进行超前水平旋喷桩预加固施工，桩长18 m，桩径0.6 m，咬合0.1 m，范围为上台阶下部处(上台阶顶部由于有部分砂卵石未施工旋喷桩);三台阶施工，上台阶为6.5 m，中台阶为2.5 m，下台阶为2 m，3个台阶跟进长度10 m，开挖进尺为0.7 m，计算中设定为1 m;开挖完成后跟进初支，并施工锁脚旋喷桩;锁脚旋喷桩长8 m，施工在上台阶和中台阶脚处;仰拱跟进距离为35 m，步距5 m;等初支变形基本稳定后再进行二衬施工，因此二衬对隧道结构的受力影响不大，计算中暂不考虑。

4.2 计算结果分析

计算模型见图7，由于模型沿x=0对称，因此选取右半侧的模型进行计算。模型水平方向半长40 m，上、下各40 m，轴向长80 m，共计28 960个单元，31 671个节点，3 426个结构单元和1 895个节点。主要模拟掌子面封闭后，仰拱跟进的施工过程，仰拱共开挖4次，依次为4 m、3 m、3 m、8 m，计算模型如图7所示，共分为5种工况。

图7 计算工况示意图

建模过程中，掌子面5个测点不在单元节点上，采用差分的原理，取两个单元的差分值，由于1号点和2号点布设位置基本对称，计算挤出变形时，是用两组相同的节点差分的，所以1号点和2号点的数值相同。在仰拱跟进施工过程中，掌子面测点的挤出变形曲线如图8所示，从图8中可以看出:数值计算的挤出变形的数值与本文测量得到的数值接近;掌子面上方部位的挤出变形比下方的部位的挤出变形要大;在仰拱每次开挖的长度与掌子面的挤出变形值正相关，单次开挖长度越长，挤出变形越大。以上3点与监测结果分析相吻合，进一步说明了监测结果分析的可靠性。

由于模型长度的原因，本文只取到掌子面前方4组监测断面的拱顶沉降数据，在仰拱跟进施工过程中，隧道拱顶沉降曲线如图9所示。从图9中可以看出:数值计算的拱顶沉降的数值与本文测量得到的数值相近;越靠近掌子面，拱顶沉降的数值越大;在仰拱每次开挖的长度与监测断面的拱顶沉降值正相关，单次开挖长度越长，拱顶沉降变形越大。

根据数值计算结果，做出各个监测断面拱顶沉降与掌子面挤出变形数值的相关曲线，如图10所示，其中，掌子面挤出变形值，取的是每种工况下掌子面5个测点挤出变形的平均值。从图10中可以看出:掌子面挤出变形与拱顶沉降变形近似呈线性关系;随着监测断面距掌子面的距离越近，曲线的斜率越大，也就是说相关程度越高。这与本文对监测结果分析是一致的，进一步验证了掌子面挤出变形和拱顶沉降变形之间存在较高的相关性。

图8 挤出变形曲线

图9 拱顶沉降变形曲线

图10 拱顶沉降变形与挤出变形相关曲线

5 结论

本文以某软弱砂质围岩隧道为研究背景，采用理论分析、监控量测和数值计算等研究手段，研究了在整个掌子面封闭后仰拱跟进期间掌子面挤出变形规律，对掌子面挤出变形和拱顶沉降变形之间的相关性进行了分析，分析结果表明:

(1)掌子面上方位置的挤出变形值要比下方位置的挤出变形值大。

(2)仰拱施工距掌子面的距离L＞4R时，施工对掌子面挤出变形影响很小，可以忽略;仰拱施工距掌子面的距离2R＜L＜4R时，随着L的减小，掌子面挤出变形持续增大，在L≈3R处，累计变形速率发生变化，变化速率增大;仰拱施工距掌子面的距离L＜2R时，随着L的减小，累计变形呈减小趋势，下降速率快。

(3)数值模拟结果表明:在仰拱每次开挖的长度与掌子面的挤出变形值正相关，单次开挖长度越长，挤出变形越大;另外，通过数值计算，得出了掌子面挤出变形与拱顶沉降变形相关曲线，在此基础上，可以通过对掌子面后方拱顶沉降变形值来估算掌子面的挤出变形值，从而对掌子面的稳定性进行评估。

(4)数值模拟和实测结果表明:掌子面挤出变形与拱顶沉降变形之间近似线性相关，挤出变形越大，则拱顶沉降变形越大，因此，可以通过采取针对掌子面的加固措施来控制拱顶的沉降变形。

[1]Pietro L.The Design and Construction of Tunnels Using the Approach Based on the Analysis of Controlled Deformation in Rocks and Soils[J］.Tunnels ＆ Tunneling International ADECO-RS Approach，2000(5):3-30.

[2]Lunardi P，Bindi R.The Evolution of Reinforcement of the Advance Core Using Fibre Glass Elements for Short and Long Term Stability of Tunnels Under Difficult Stress-strain Conditions:Design，Technologies and Operating Methods[C］∥Progress in Tunnelling after 2000:Proceedings of the AITES-ITA 2001 World Tunnel Congress，Milan-Italy 10th-13th June 2001.Bologna:Patron Editore，2001，2:309-322.

[3]Lunardi P.The ADECO-RS Approach in the Design and Construction of the Rome to Naples High Speed Railway Line:a Comparison Between Final Design Specifications，Construction Design and‘As-built’[C］∥Progress in Tunnelling after 2000:Proceedings of the AITES-ITA 2001 World Tunnel Congress，Milan-Italy 10th-13th June 2001.Bologna:Patron Editore，2001，3:329-340.

[4]Lunardi P，Silva C，Focracci A.The Bologna to Florence High Speed Railway Line:92 km through the Appennines[C］∥Progress in Tunneling after 2000:Proceedings of the AITES-ITA 2001 World Tunnel Congress，Milan-Italy 10th-13th June 2001.Bologna:Patron Editore，2001，3:341-351.

[5]Gattinoni P，Papini M，Scesi L.Geologic Risk in Underground Works[C］∥Progress in Tunnelling after 2000:Proceedings of AIWES-ITA 2001 World Tunnel Congress，Milan-Italy 10th-13th 2001.Bologna:Patron Editore，2001，1:309-318.

[6]王树栋，刘开云.长大隧道软弱围岩施工大变形智能预测方法[J］.中国铁道科学，2008(2):82-87.

[7]管振祥.富水土质隧道变形规律的试验研究[J］.石家庄铁路工程职业技术学院学报，2003，2(2):45-49.

[8]刘波，曹波，刘芳，等.北京地铁暗挖隧道变形监测与稳定性数值分析[J］.地下空间与工程学报，2011，7(3):518-525，540.

[9]王淑芳.软岩隧道变形动态监测与分析[J］.中国水运，2011，11(6):220-222.

[10]肖广智，魏祥龙.意大利岩土控制变形(ADECO-RS)工法简介[J］.现代隧道技术，2007，44(3):11-15.

[11]陈帆，傅星，李梦超.基于隧道效应的振动检测反馈系统设计[J］.河南科技大学学报:自然科学版，2008，29(4):77-79.

[12]马国强，杨宗霄，王少波.基于东方系统方法论的隧道安全评价[J］.河南科技大学学报:自然科学版，2011，32(3):42-46.

[13]刘招伟，赵运臣.城市地下工程施工监测与信息反馈技术[M］.北京:科学出版社，2006.