基于多高斯窗的实值离散Gabor变换

李 锐，陶 亮

安徽大学 计算智能与信号处理教育部重点实验室，合肥 230039

基于多高斯窗的实值离散Gabor变换

李 锐，陶 亮

安徽大学 计算智能与信号处理教育部重点实验室，合肥 230039

1 引言

Gabor变换是重要的时频分析方法之一[1]。Gabor变换的重要特点在于Gabor变换系数揭示了信号在时域与频域的局部化性，Gabor变换的优点已被用于非平稳信号的处理，如生物医学信号的分析与处理、信号的检测、图像压缩、图像识别、线性时变系统建模等方面。然而，由于传统复值离散Gabor变换算法具有较高的计算复杂性，从而限制了其实时应用。另外，传统复值离散Gabor变换是单窗的，具有固定的时频分辨率这一缺点。由于受窗函数时宽-带宽之间的制约关系，也即不确定性原理[2]限制，传统单窗复值离散Gabor变换时间分辨率和频率分辨率是矛盾的关系，不可能同时都好。为了改善传统离散Gabor变换时频分辨率并加快其变换速度，本文在文献[3]基础上提出了一种基于多高斯窗的实值离散Gabor变换。实值离散Gabor变换有快速算法[4]，其变换系数与复值离散Gabor变换系数的实部和虚部有着非常简单的加减关系，因此能大大减少复值离散Gabor变换系数计算量。实验结果表明，基于多高斯窗的实值离散Gabor变换能得到较好时间和频率的分辨率，明显改善联合时频域内的聚集性，更适用于非平稳信号的处理。

2 传统离散Gabor变换回顾

2.1 单窗复值离散Gabor变换

x(k)为一个有限长或者经过周期拓展的时间序列，周期为L。传统的单窗离散Gabor展开式定义[5]为：

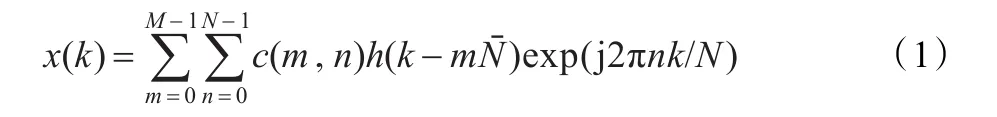
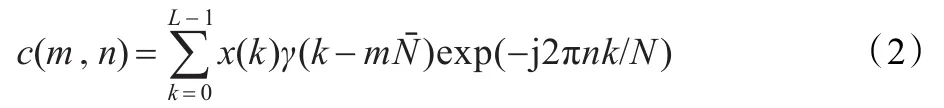
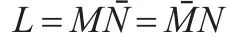
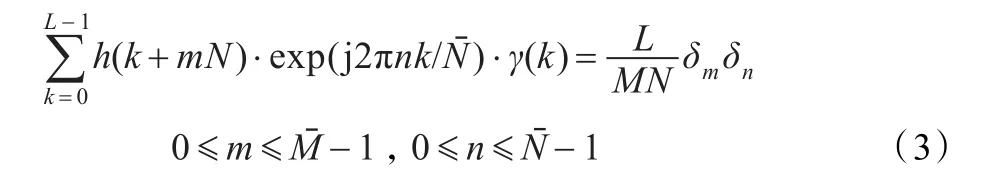
其中δk={1,k=0 0,k≠0，给定的综合窗h(k)就可以由此式求出双正交分析窗γ(k)。

2.2 多窗复值离散Gabor变换

设x(k)为有限长或者截断的进行周期拓展的时间序列，周期为L，那么基于多高斯窗下的Gabor展开式[1]定义为：

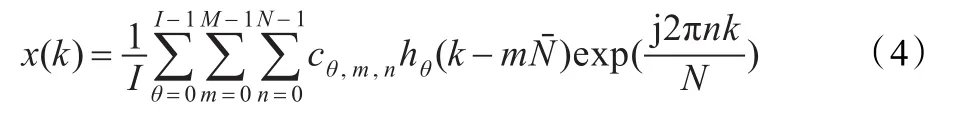
其中 j= -1，系数cθ，m，n可由以下公式获得：

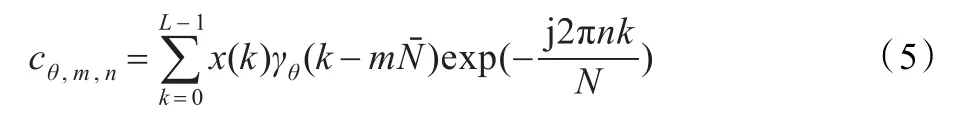
这里I，M，N分别为窗函数的个数，时间和频率的采样点数。M，N，L的关系及完备性条件与2.1节的传统离散Gabor变换的约束条件和关系一样，这里就不多叙述了。其中：

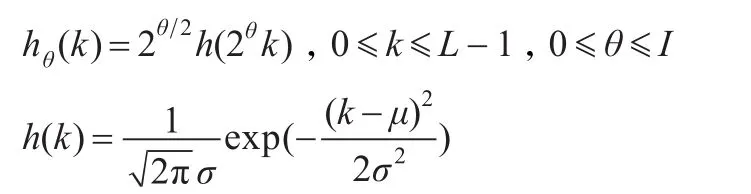
h(k)为高斯窗函数，在这里称为母窗，hθ(k)称为子窗。传统的离散Gabor变换是单窗下进行的，具有固定的时间和频率的分辨率，由于受到时宽-带宽的不确定性原理限制，在单窗条件下离散Gabor变换的时间和频率分辨率是成反比的，不可同时做到都好。由公式（4）和公式（5）可以看出将信号在一组窗函数下分解，由于平均的作用，其时间和频率分辨率可同时得到有效改善。

3 基于多高斯窗的实值离散Gabor变换

3.1 单窗实值离散Gabor变换

将长度为L的信号拓展或截断成周期为L的序列x(k)，实值离散Gabor展开和Gabor变换系数分别定义为式（6）和式（7）[4]。

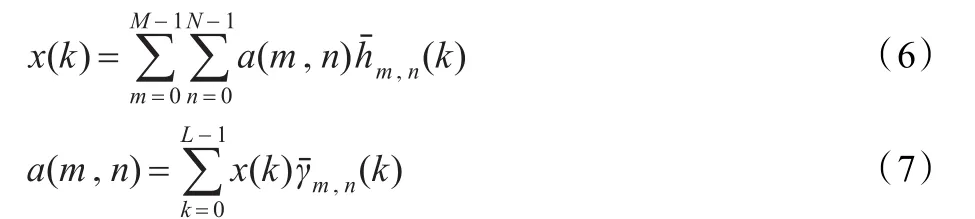
公式（6）称为实值离散Gabor变换，其中：

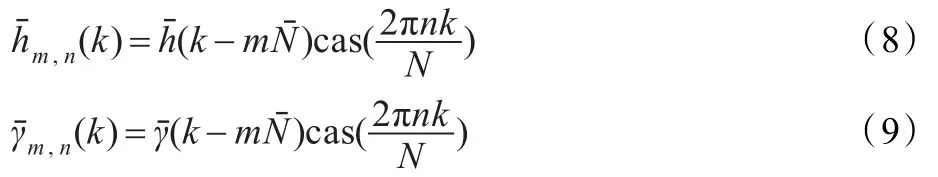
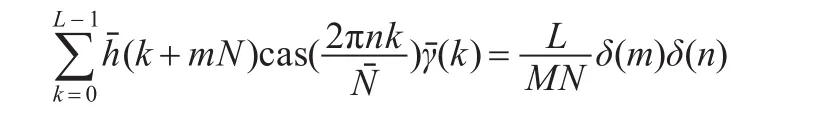
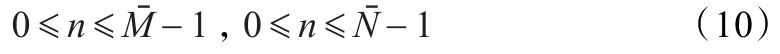
3.2 多高斯窗实值离散Gabor变换

在文献[3]方法基础上，利用实值离散Gabor变换取代复值离散Gabor变换，即可得到基于多高斯窗的实值离散Gabor变换，这样既可改善Gabor变换时频分辨率，又可加快Gabor变换速度，适应实时处理需求。基于多高斯窗的实值离散Gabor展开式和变换式分别定义为[3-6]：

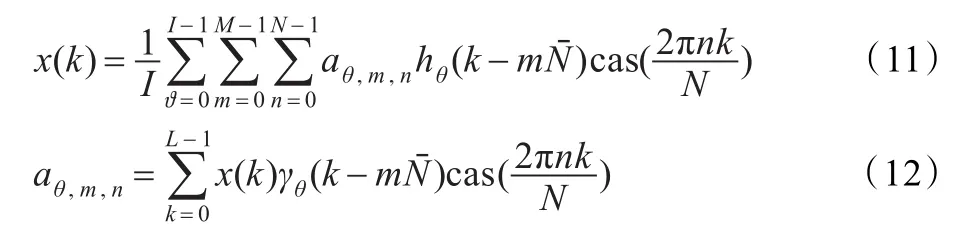
其中hθ，m，n(k)和γθ，m，n(k)要满足双正交的完备性关系公式：

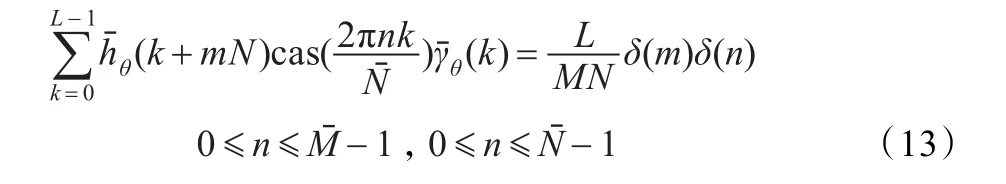
通过公式（12）可以看出是把信号在多组高斯基函数上进行分解，进行不同尺度的分解，然后求平均来还原信号，可以得到不同时间和频率尺度的Gabor展开（变换）系数，克服了固定窗函数的缺点。

4 进化谱分析

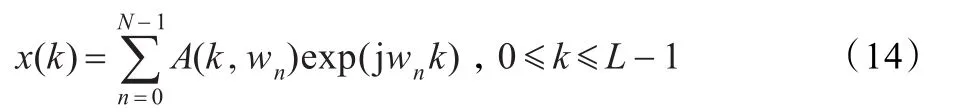
传统的确定性信号可表示如下：是时间-频率核，并由如下公式获得：

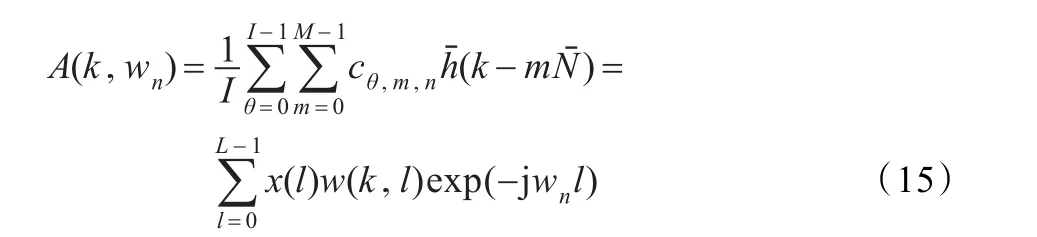
其中cθ，m，n是基于多高斯窗的下的复值Gabor变换系数。定义：

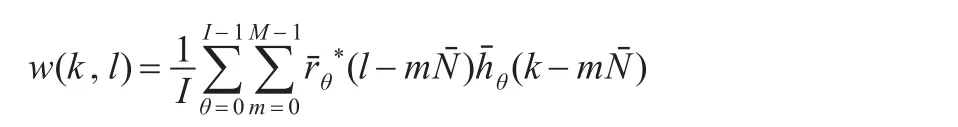
为时间变化窗。图1为w（k，64）的时间变化窗，对应的幅度频谱图如图2所示。

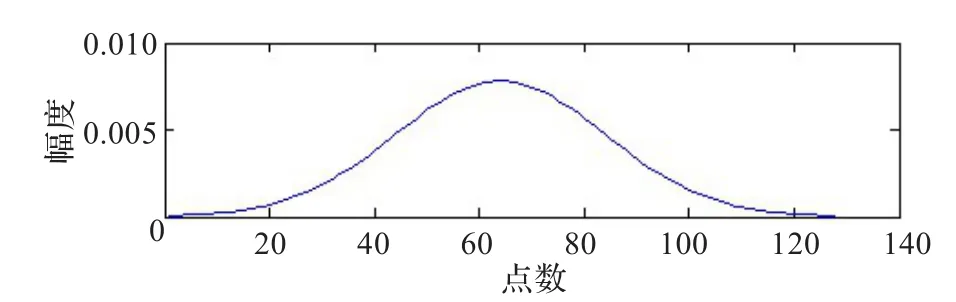
图1 w（k，64）时间变化窗

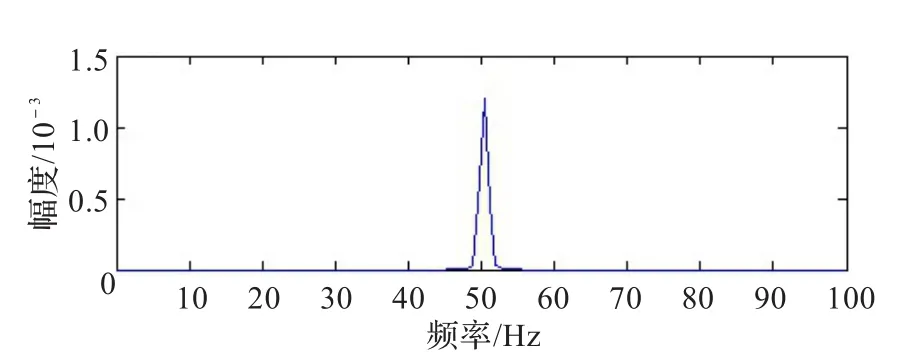
图2 w（k，64）的频谱图

从图1和图2可以看出时间变化窗在时间和频率都有良好的分辨率而且很平滑，对信号分解可以得到比较好的时间和频率的分辨率，时变窗的三维图形如图3所示。

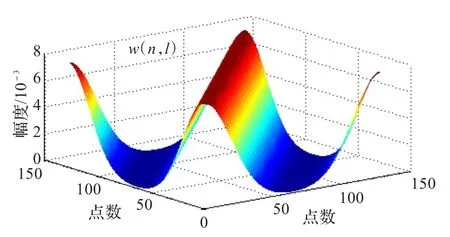
图3 时变窗三维图

x(k)的进化谱定义为：

A(k，wn)是复函数，可用多高斯窗下的实值Gabor变换简化计算，为此可将式（15）改写如下：

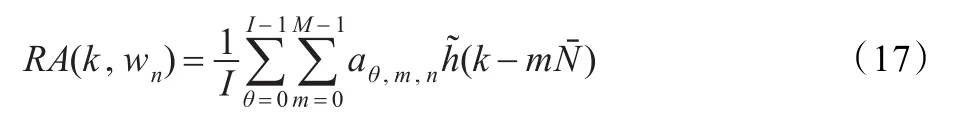
其中aθ，m，n为多高斯窗下的实值离散Gabor变换系数，可由式（12）获得。再将式（16）改写如下：

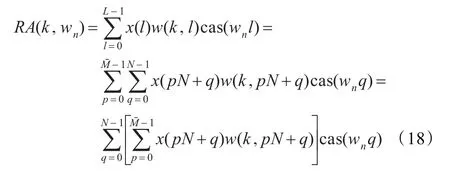
不难看出，式（18）可通过使用N点离散Hartley变换（DHT）快速算法计算。根据实值Gabor变换系数与复值离散Gabor变换系数关系，不难导出A(k，wn)与RA(k，wn)的关系如下：

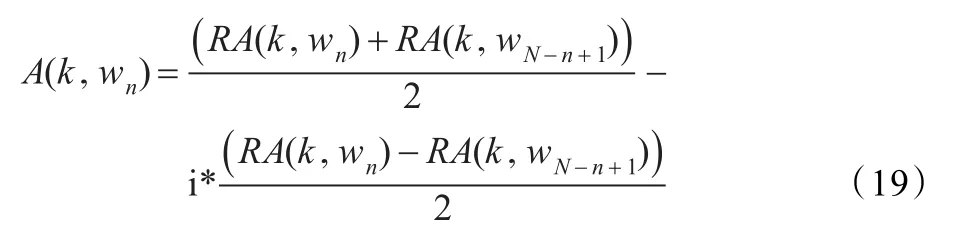
由于实值运算速度快于复值运算速度，所以能加快信号分析的过程。

5 实验

非平稳信号是指分布参数或者分布律随时间发生变化的信号并且统计特征是时间的函数，一般的分析方法是时频联合分析。心电图检查是临床常规检查项目之一，其对于心脏疾病的及早发现及治疗具有重要的意义。医生从心电图中得到所需的临床信息，根据这些信息对病人作出诊断。心电图到动态心电图，其过渡的一个关键是心电信号临床信息的自动识别，即心电信号分析技术。目前的心电图自动分析并不能完全取代人工分析，大多只用来辅助心电专家对病人进行诊断，其主要原因是现有的心电自动诊断技术精度不够，不能完全达到临床应用的要求。因此提高对心电信号分析的准确性和实用性，对实现自动化分析有着非常重要的意义。

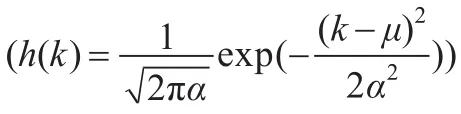
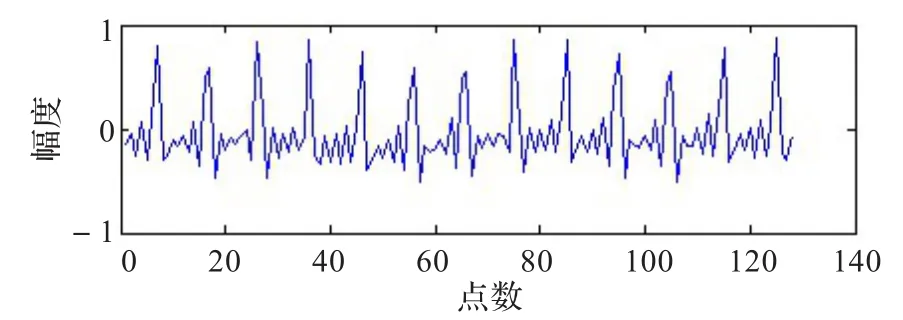
图4 EKG（心电信号）信号

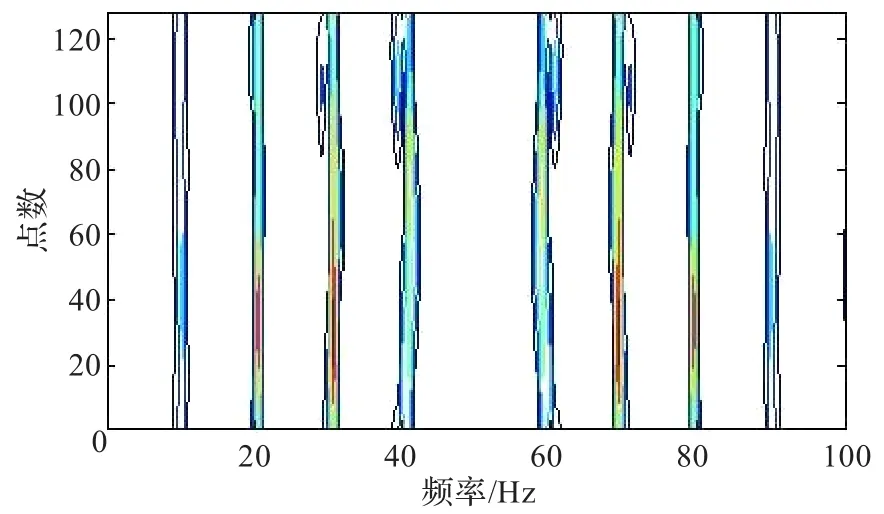
图5 宽高斯窗下谱图

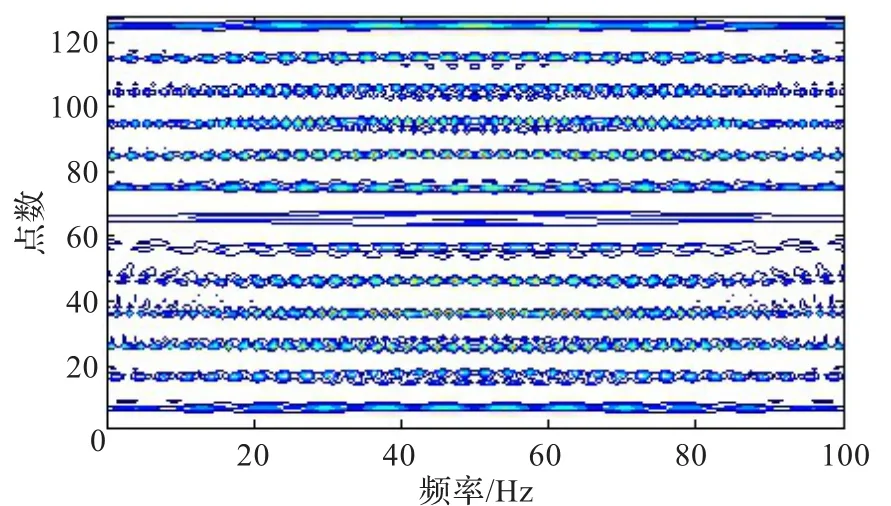
图6 窄高斯窗下时频谱图

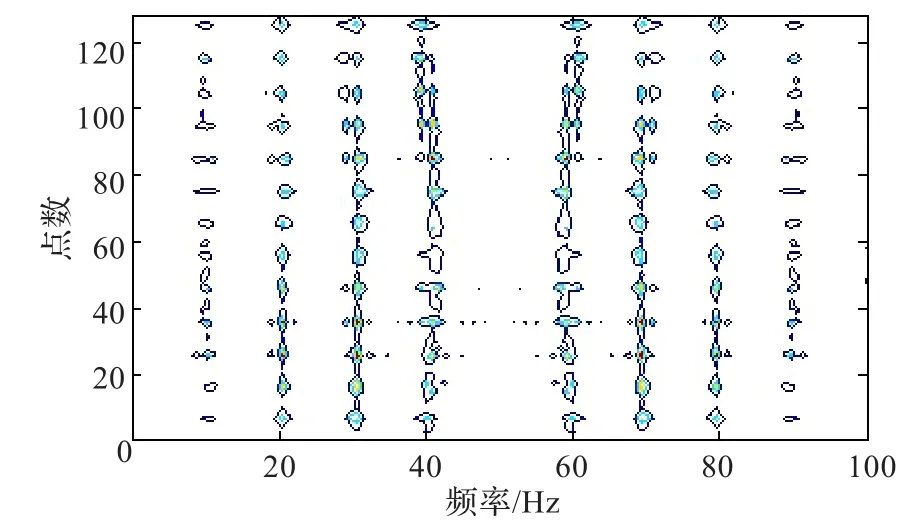
图7 多高斯窗下进化谱图

6 总结

针对传统的单窗复值离散Gabor变换具有固定的时频分辨率，文献[3]提出的基于多高斯窗的复值Gabor变换得到的进化谱虽然时频精度高但是由于其变换是基于复值因此速度慢。本文提出了一种基于多高斯窗的实值离散Gabor变换，不仅改善了离散Gabor变换时频分辨率还加快了其变换速度，从而提供了一种快捷地计算非平稳信号（高时频分辨率）进化谱（时频谱）方法。图7可以看出信号在时频域内有良好的聚集性，有较好的实用性。仿真实验表明基于多高斯窗的实值Gabor变换既能得到较高的时频聚集性而且计算复杂度小。

[1]GaborD.Theory ofcommunication[J].JInstElectrEng，1946，93（3）：429-457.

[2]Cohen L.Time-frequency analysis[M].Englewood Cliffs，NJ：Prentice-Hall，1995.

[3]Akan A，Chaparro L F.Multi-window Gabor expansion for evolutionary spectral analysis[J].Signal Processing，1997，63 （1）：249-262.

[4]陶亮，顾涓涓.实值Gabor变换理论及应用[M].合肥：安徽科学技术出版社，2005.

[5]Qian S，Chen D.Discrete Gabor transform[J].IEEE Transactions on Signal Processing，1993，41（7）：2429-2438.

[6]Wang L，Chen C T，Lin W C.An efficient algorithm to compute the complete set of discrete Gabor coefficients[J]. IEEE Trans on Image Processing，1994，3（1）：87-92.

LI Rui,TAO Liang

MOE Key Lab of Intelligence Computing and Signal Processing,Anhui University,Hefei 230039,China

The traditional single-window based discrete Gabor transform has a fixed joint time-frequency resolution.Due to the uncertainty principle the time resolution and frequency resolution in the Gabor transform domain have an inverse proportion relationship.In order to improve the joint time-frequency resolution of the traditional discrete Gabor transform and speed up the transform,it presents a multi-Gaussian window based real-valued discrete Gabor transform.The experimental results show that the proposed transform can effectively improve the accuracy of the joint time-frequency resolution,it provides a fast method for the computation of the evolutionary spectrum of the non-stationary signals with the high joint time-frequency resolution.

real-valued discrete Gabor transform;time-frequency signal analysis;evolutionary spectrum

传统的单窗复值离散Gabor变换具有固定的时频分辨率，由于受窗函数时宽-带宽之间的制约关系，即不确定性原理限制，其时间分辨率和频率分辨率是矛盾的关系。为了改善传统离散Gabor变换时频分辨率并加快其变换速度，提出了一种基于多高斯窗的实值离散Gabor变换，实验结果表明能有效改善联合时频域内的聚集性，从而提供了一种快捷地计算非平稳信号进化谱方法。

实值离散Gabor变换；时频分辨率；进化谱

A

TP391

10.3778/j.issn.1002-8331.1107-0463

LI Rui,TAO Liang.Multi-Gaussian window based real-value discrete Gabor transform.Computer Engineering and Applications,2013,49（5）：210-212.

国家自然科学基金（No.61071169）；安徽大学创新研究项目（No.yqh090053）。

李锐（1986—），男，硕士研究生，主要研究领域为信号处理；陶亮（1963—），男，博士，教授，主要研究领域为信号处理、模式识别等。E-mail：lirui4788503@163.com

2011-07-22

2011-12-26

1002-8331（2013）05-0210-03