欠驱动船舶的运动规划和全局指数跟踪控制

王 岩，朱齐丹，刘志林，杨 震

哈尔滨工程大学 自动化学院，哈尔滨 150001

欠驱动船舶的运动规划和全局指数跟踪控制

王 岩，朱齐丹，刘志林，杨 震

哈尔滨工程大学 自动化学院，哈尔滨 150001

1 引言

近年来，欠驱动系统的运动控制问题一直是倍受关注的研究热点。欠驱动水面船舶（Underactuated Surface Vessels，USV）由于横向上未装备驱动装置，缺少可用的控制输入，因此针对一般运动系统的基于向量的控制器设计方法不能有效地用以解决USV的运动控制问题[1-2]。欠驱动船舶执行跟踪敌对目标、巡逻勘察、近远程避障等作战任务时，均需要以一定的速度沿着指定的目标航迹航行。因此航迹跟踪控制系统是USV使命中重要的组成部分。在航迹跟踪控制器设计过程中，期望连续可导的目标信号，然而在实际中这种连续可导的目标航迹是难以指定的，甚至是不可实现的，比如在避障控制中目标航迹是复杂多变的，如此连续多变的目标航迹几乎是难以设计的。即使在执行简单的航迹跟踪任务中，连续的目标航迹可以给出，此时设计出来的航迹跟踪控制器也无法具有普遍意义，难以推广到操纵性、实时性和路况复杂多变的环境中。因此设计离散目标点指导下的航迹跟踪控制方法就成为实现USV航迹跟踪控制的迫切需要，并可广泛应用到多种操纵控制任务中。而运动规划算法可以将离散的目标位置点转为期望的连续航迹信号和符合安全运动约束的期望姿态信息，可兼顾实用性和控制器设计方便的双重需要。

目前对于USV的航迹跟踪的研究，主要存在两条不同的研究路线：一种是基于虚拟指导船舶的航迹跟踪控制方法[3-8]，另外一种是基于运动学和动力学回路的跟踪控制方法。所谓的虚拟船舶是指控制器设计中存在一个虚拟运动的船舶，该船舶的附加质量和水动力系数与实际受控船舶一致，在期望的纵向推力和转向力矩驱动下由虚拟指导船舶实时产生实际受控船舶的操纵运动可物理实现的期望航迹和期望运动姿态。虚拟船舶方法存在的主要问题是：由于难以预知复杂的期望航迹的参考控制输入，导致所设计的航迹跟踪控制器难以跟踪任意指定航迹，即使是操纵运动可实现的。因此，文献[3-8]在仿真或实验都是跟踪一条指定的圆或圆弧航迹。但优势为不仅可以跟踪指定的位置变量，还可以同时实现对艏摇角、艏摇角速度、纵向速度、侧向速度的姿态跟踪。基于运动学和动力学回路的跟踪控制方法仅仅能够实现USV的期望位置跟踪，不能实现其他姿态的跟踪[9-10]。而且也未能解决关于在未知复杂的环境下如何得到符合安全运动约束和动力学条件约束的连续期望航迹问题。

从工程角度出发，为实现欠驱动船舶的航迹跟踪控制器应用于实际问题，本文主要由以下几部分组成：首先，为解决欠驱动船舶不能跟踪任意指定航迹问题，运用运动规划方法，利用离散目标点规划出符合动力学约束的连续期望轨迹；其次，引入微分同胚变换，建立两个级联子系统构成的航迹跟踪误差动态方程，并运用反步法对变换后的误差子系统设计了全局指数状态反馈控制律。最后利用本文提出的基于规划期望轨迹的全局指数航迹跟踪控器进行了仿真实验，结果表明所提出的方法能有效地实现USV航迹的精确跟踪。

2 欠驱动船舶的运动模型

考虑如下欠驱动水面船舶模型[11]：

3 规划期望航迹

运动规划算法以离散的目标位置点为基本信息，通过样条函数对目标位置点进行分段拟合，不仅输出分段连续的期望航迹，同时输出具有安全运动约束的目标姿态，形成航迹跟踪控制器有效的期望输入，从而实现姿态约束及安全运动约束条件下的USV航迹跟踪控制，既能充分发挥USV优良的操纵性能，又能实现良好的跟踪控制性能。

基于运动规划的USV航迹跟踪控制分为4个步骤：

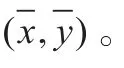
（2）根据连续化航迹信息，估计USV的姿态信息(-u,-v,-ψ,-r)。

（3）利用动力学特性获得期望的控制输入(τ1d，τ3d)，由此确定被跟踪的期望姿态(xd，yd，ψd，ud，vd，rd)。

（4）设计航迹跟踪控制器，跟踪期望姿态(xd，yd，ψd，ud，vd，rd)。

3.1 参考航迹的多项式拟合

假设离散目标点 (xk-1，yk-1)、(xk，yk)和 (xk，yk)、(xk+1，yk+1)分别存在曲线Sk-1(θ)和Sk(θ)，其中θ为参考期望轨迹参数。

定义向量θVEC为：

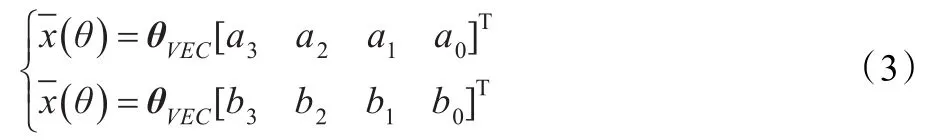
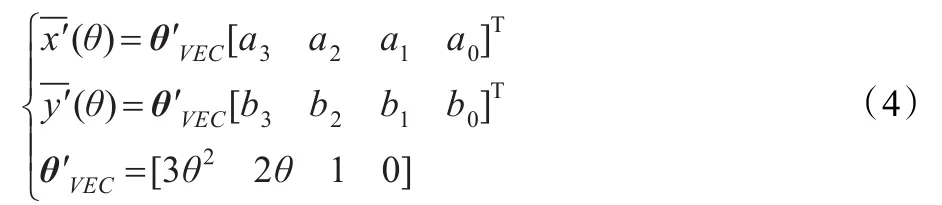
因此，根据式（1），大地坐标系下的船速Ud() t为：

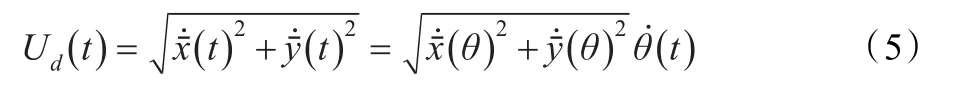
若船舶航速的动态特性可以表征为：

式（5）和（6）联立，可知θ(t)和Ud(t)的动态变化过程为：

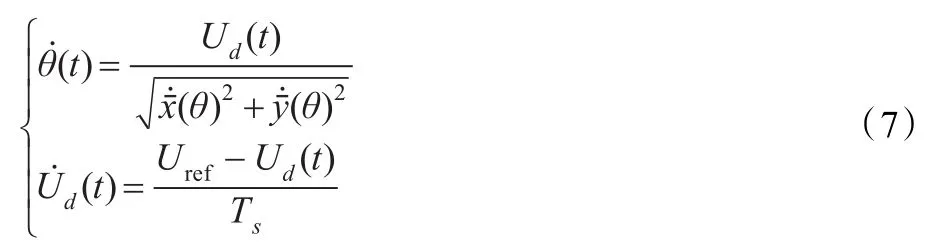
其中，Uref为参考速度，Ts为速度动态时间常数。

下面需要根据连续性条件确定目标航迹的轨迹参数[a3a2a1a0]T和[b3b2b1b0]T。

易知，若存在N+1个点，则存在N个曲线S，也即存在4N个参数对(a，b)。因此，需要建立4N个约束方程，以确定拟合参数。

这里，以某连续的三个离散点为例，存在连续曲线Sk-1(θ)和Sk(θ)，应满足连续性条件为：

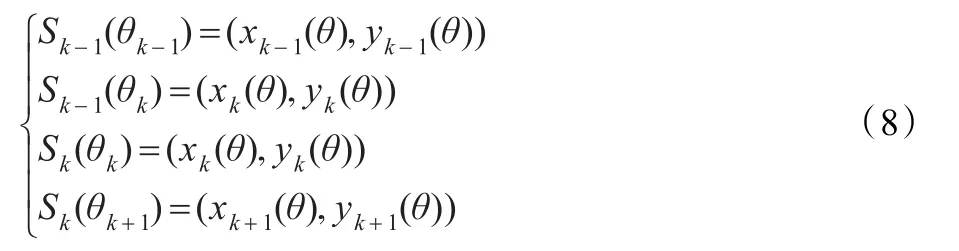
若Sk-1(θ)和Sk(θ)对轨迹参数变量θ的一阶和二阶导数满足连续条件：

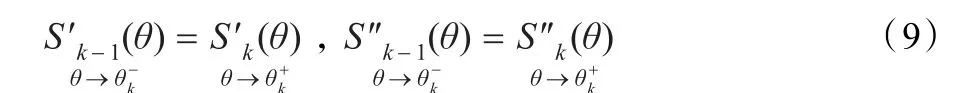
因为连续性及可导性条件是对于单点阐述的，因此除首尾两个点外，可以建立4(N-1)个方程。同时，首尾点位于首尾曲线S1(θ)和SN(θ)上并满足可导性条件，这样一共可建立4N个约束方程，由此可确定式（3）中的4N个轨迹参数。

3.2 参考姿态的估计

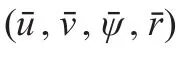
考虑USV已跟踪上目标轨迹，根据式（1）可知：

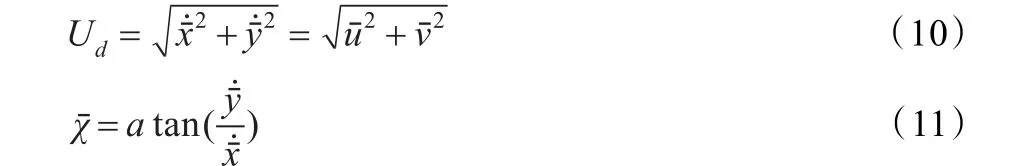
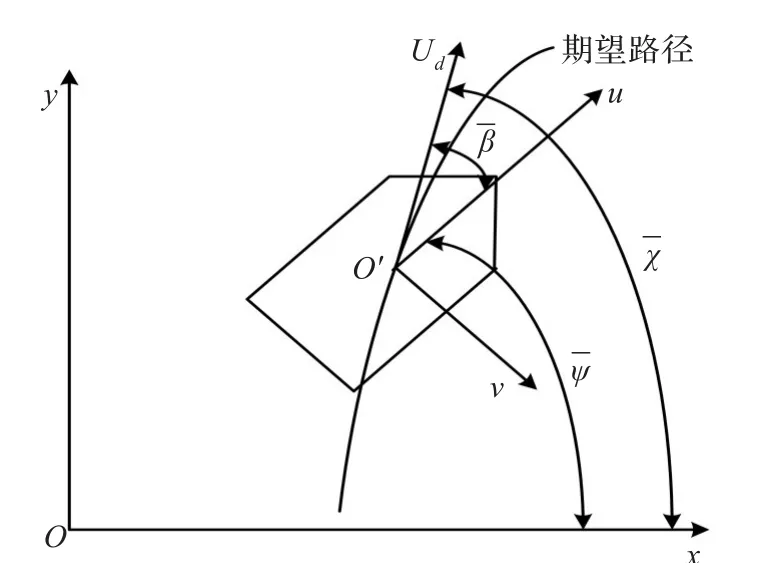
图1 航迹向、真航向和漂角三者间关系

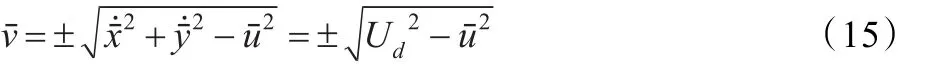
式（15）的微分结果为：

同时，根据式（15）可知：

根据式（14），结合式（10）、（13）和（15）可以计算得出当轨迹不为直线时，角速度的计算公式为：

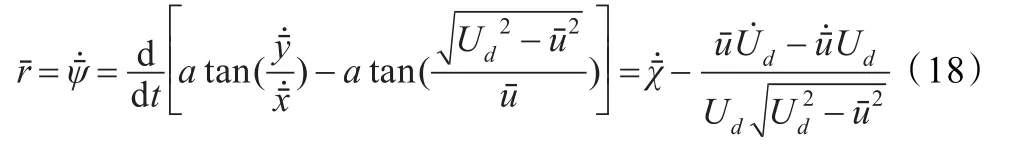
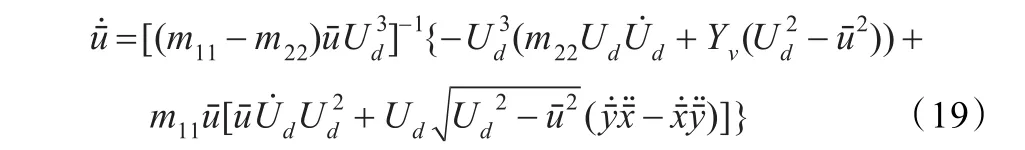
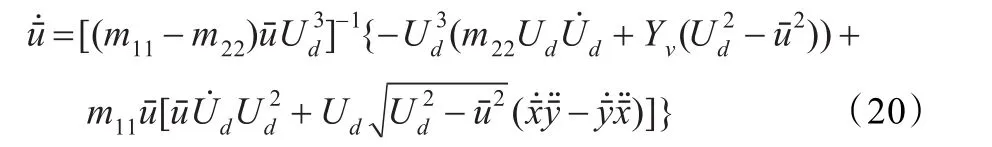
至此，可以总结船舶参考状态的估算过程：首先，根据已知参考航迹和，通过式（19）和（20）能够计算得出USV纵向速度，之后根据式（15）计算得到侧移速度，最后根据式（14）和（18）计算得到航向角和航向角速度。

3.3 期望控制输入的规划

前面两节已经给出USV运动可行的连续参考轨迹、航向角和船体坐标系下的所有速度和加速度，下面将利用USV的动力学模型（1）直接计算得出相应开环期望控制输入：

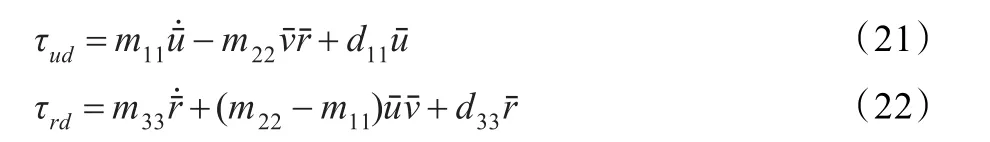
将式（21）和（22）中的期望控制输入(τud，τrd)代入整个运动方程（1），可求得USV的操作性可实现的期望航迹(xd，yd，ψd，ud，vd，rd)。

运动规划算法和开环控制律（21）、（22）可以看作是设计闭环轨迹跟踪控制律的一部分。当USV在跟踪轨迹上，且模型精确，同时不存在外界干扰时，开环控制律（21）、（22）能有效保证USV的精确跟踪。但是，由于模型的不确定性等原因，需要设计带有反馈的闭环控制率以保证USV的精确跟踪。

4 指数跟踪控制器设计

由上章可得根据期望点所设计的物理可实现期望轨迹(xd，yd，ψd，ud，vd，rd)和期望输入(τ1d,τ3d)，满足：

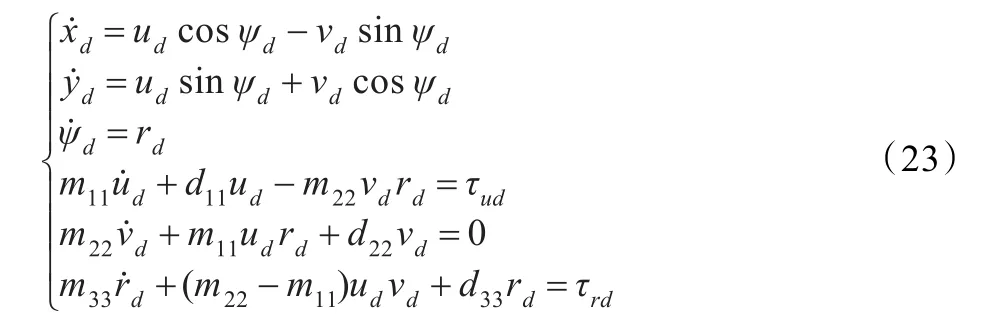
4.1 控制目标的分解简化

为利于控制器设计，引入状态变换和输入变换[5]：

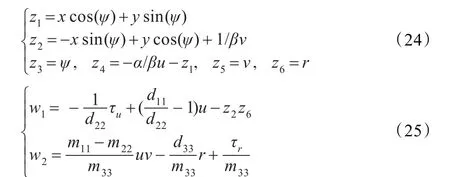
则整理后新的动态方程为：

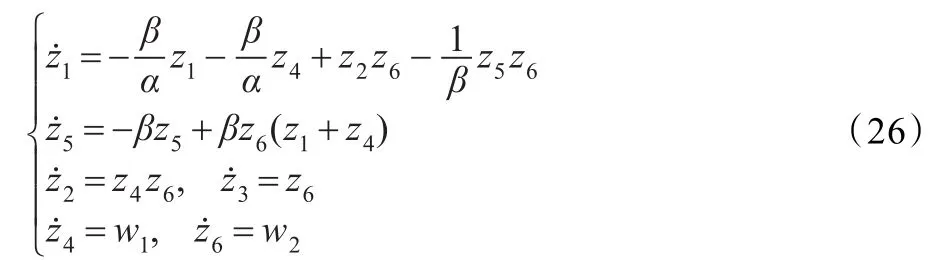
同理，经坐标变换：

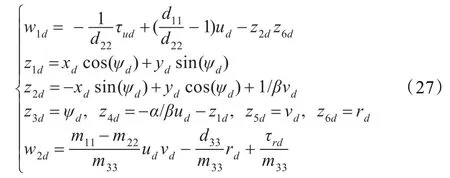
则有：

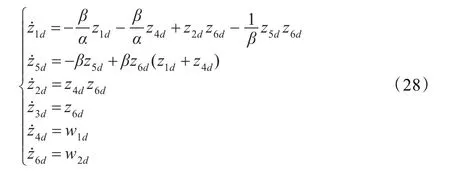
定义跟踪误差：

则有：

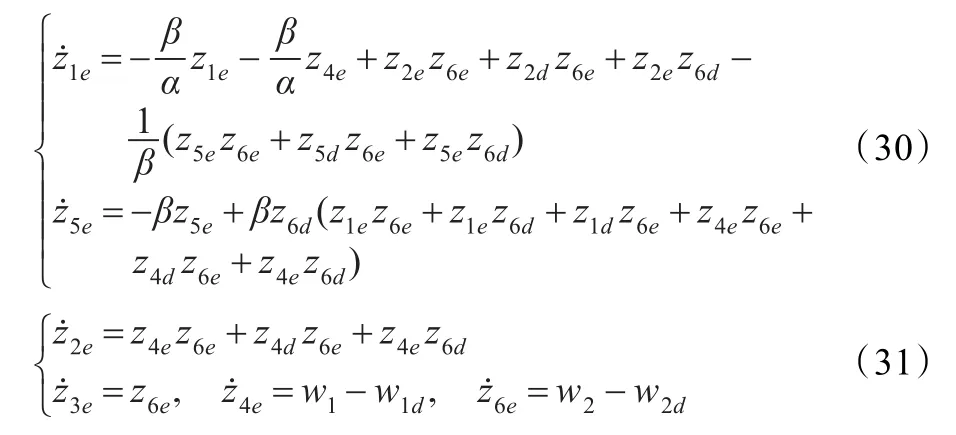
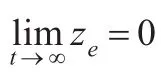
引理1[6]如果存在一种控制律使得系统（31）全局指数稳定，则该控制律同样能使得系统（30）全局指数稳定。

在接下来的控制器设计中，只需要考虑设计反馈控制律使得系统（31）全局指数稳定即可。

将系统（31）表示成如下两个子系统：

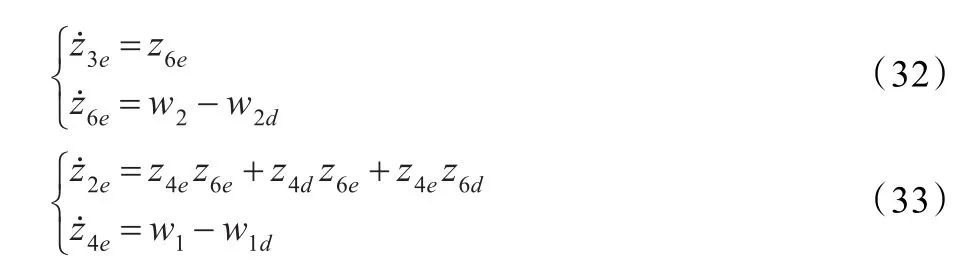
由此控制目标可通过如下两个步骤实现：

步骤1将z6e=σ看成虚拟控制输入，设计部分状态反馈控制律w2使得系统（32）全局指数稳定。

步骤2设计部分状态反馈控制律w1使得系统（33）全局指数稳定。

4.2 步骤1的实现

定理1针对线性系统（32），易构造如下控制律：使得其闭环系统全局指数稳定（GES）。

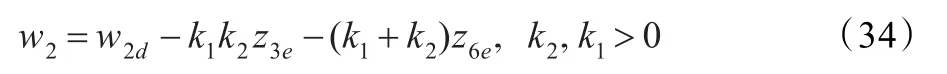
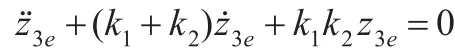
4.3 步骤2的实现

定理2对于系统（33），若rd满足标准激励条件：

其中，δ＞0，则在控制律（36）作用下的闭环系统GES。

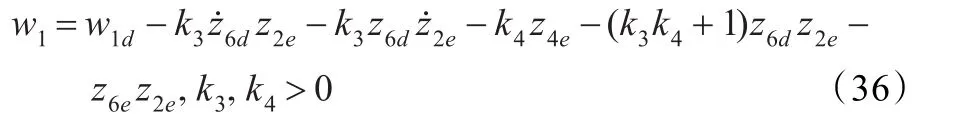
针对系统（33），定义变量σ=z4e+k3z6dz2e，z6d≠0，则有：

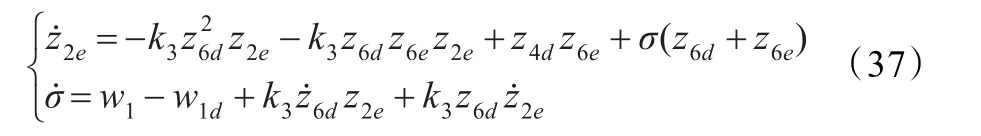
定义如下Lyapunov函数：

求导并代入控制律（36），则

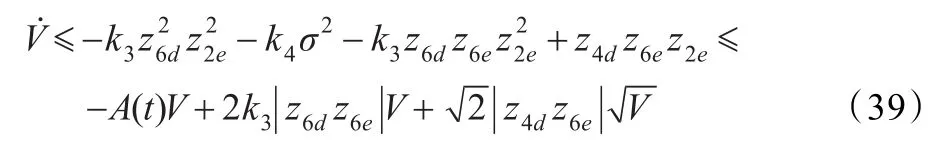
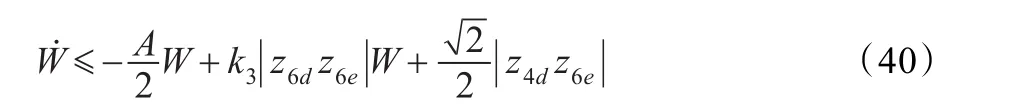
由比较定理[12]：

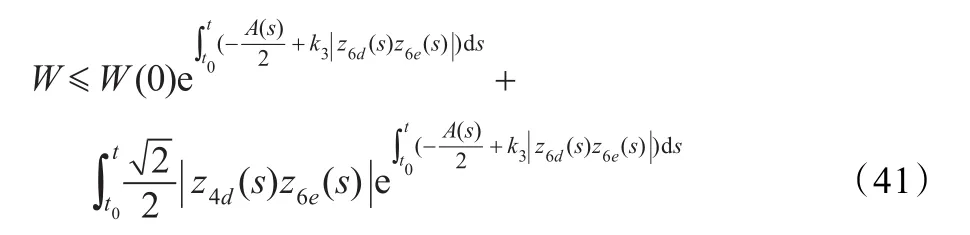
由于z4d、z6d(rd)有界，且当t→∞时，z6e→0，显然W收敛到0，因此V收敛到0，进而，当t→∞时，z2e，σ→0，因此当t→∞时，z4e→0。

4.4 控制目标的实现

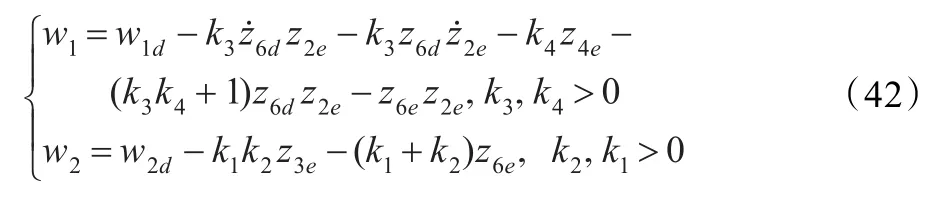
定理3在控制律：的作用下误差系统（30）和（31）的闭环系统GES。

证明 由引理1、定理1、定理2可知。

由定理3，可知ze全局指数收敛于零，则有(x-xd，y-yd，ψ-ψd，u-ud，v-vd，r-rd)全局指数收敛于零，从而实现了欠驱动船舶对任意可行航迹的全局指数跟踪控制。

5 仿真结果

将通过仿真实验验证所提控制律的实际有效性，仿真环境基于MATLAB/SIMULINK工具搭建。期望状态(xd，yd，ψd，ud，vd，rd)和船舶状态(x，y，ψ，u，v，r)经过微分同胚变换后构成了整个控制器的输入，经控制律（42）解算后得到船舶的实际控制输入，从而完成输出反馈控制律的闭环仿真验证。仿真中所选船模的参数为[5]：m11=200kg，m22=250kg，m33=80kg，d11=70kg/s，d22=100kg/s，d33= 50kg/s。船舶的初始状态设为(x(0)，y(0)，ψ(0)，u(0)，v(0)，r(0))= (0，-2，0，0，0，0)。控制律（42）中的控制参数设为k1=1，k2=1.2，k3=6，k3=1.6，满足定理3中稳定性分析中确定的参数限定条件。离散的期望点为：yk=[-0.5,0,2,2,3,4,5.5]，xk=[0，0.6，1.5，3，4，4，32]。仿真结果如图2～6所示。

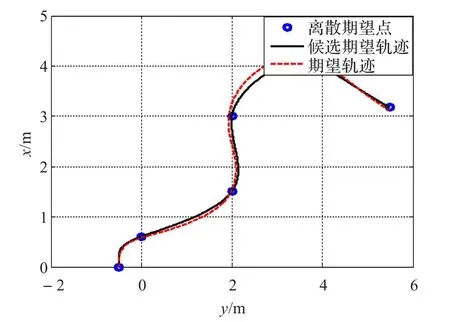
图2 规划期望轨迹

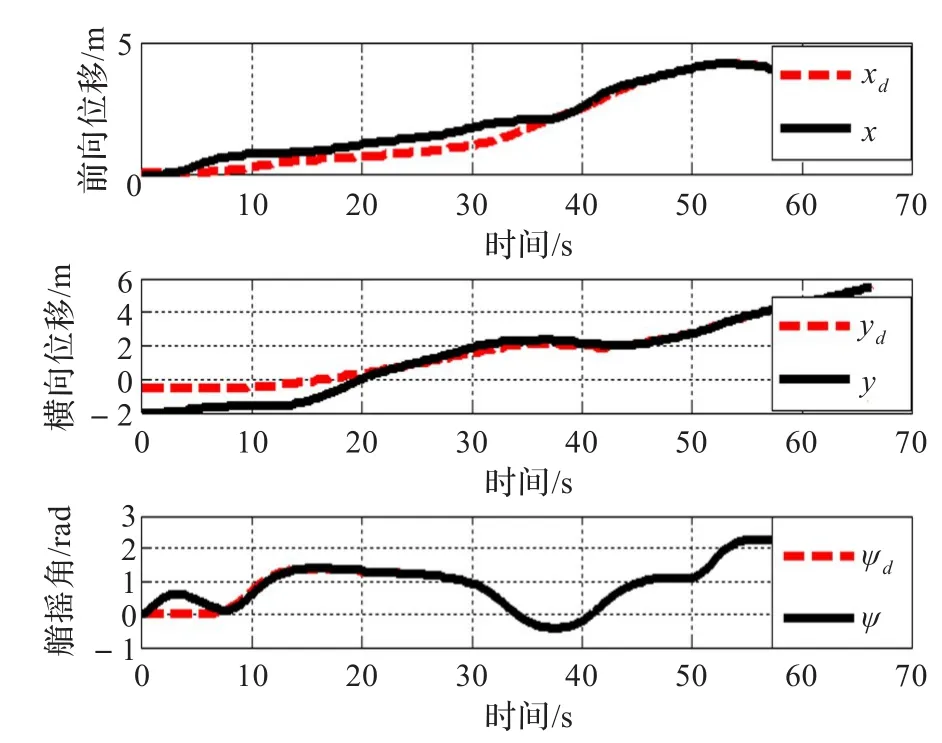
图3 船舶的实际与期望位置和艏摇响应

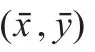
图4 船舶的实际与期望的速度和角速度响应

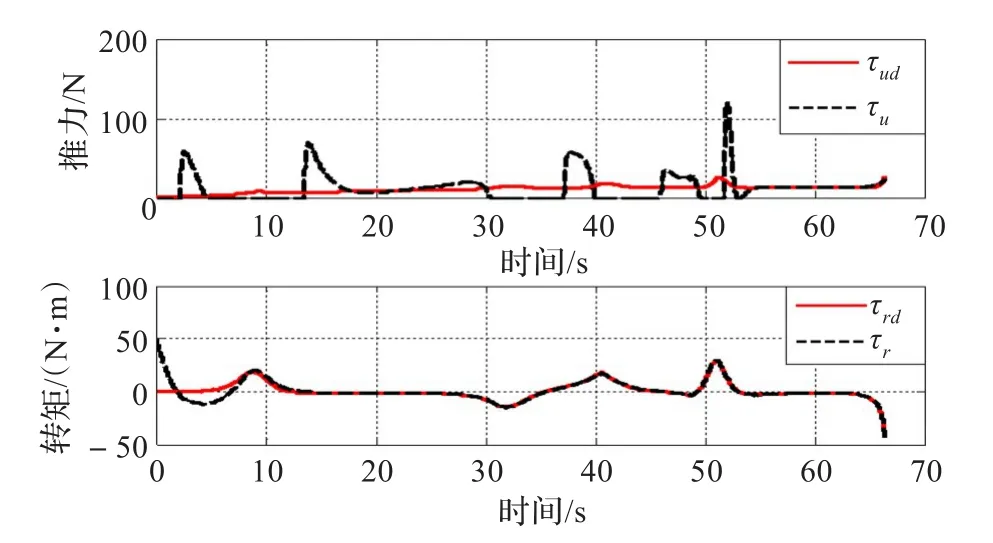
图5 实际与期望的控制输入

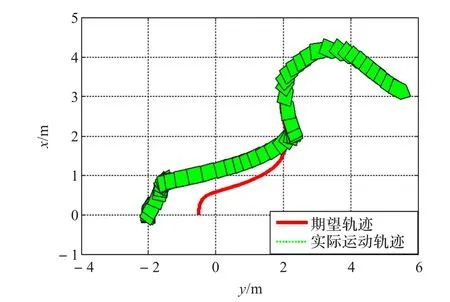
图6 实际航迹与期望航迹

6 结束语

通过对USV航迹跟踪的研究，利用多项式拟合获得连续参考轨迹，进而估计各个参考姿态；结合参考姿态和船舶动力学模型，得到期望的控制输入，进而规划出操作性可实现的全部期望姿态。同时，为实现欠驱动船舶的航迹快速跟踪控制，引入微分同胚变换，基于反步法设计原理，针对变换后的误差动态方程设计了全局指数状态反馈航迹跟踪控制律，实现了欠驱动USV在任意可行航迹条件下的全局指数航迹跟踪控制。

[1]高炳团，陈宏钧，张晓华.欠驱动机械系统控制设计综述[J].电机与控制学报，2006，10（5）：541-546.

[2]郭晨，汪洋，孙福春，等.欠驱动水面船舶运动控制研究综述[J].控制与决策，2009，24（3）：321-329.

[3]Lefeber E，Pettersen K Y，Nijmeijer H.Tracking control of an underactuated ship[J].IEEE Transactions on Control Systems Technology，2003，11（1）：52-61.

[4]Jiang Z P.Global tracking control of underactuated ships by Lyapunov's direct method[J].Automatica，2002，38（2）：301-309.

[5]Dong Wenjie，Guo Yi.Nonlinear tracking control of underactuated surface vessel[C]//American Control Conference.Portland，USA：[s.n.]，2005：4351-4356.

[6]Ghommam J，Mnif F，Derbel N.Global stabilization and tracking control of underactuated surface vessels[J].IET Control Theory and Applications，2010，4：71-88.

[7]孟威，郭晨，孙富春，等.欠驱动水面船舶的非线性滑模轨迹跟踪控制[J].哈尔滨工程大学学报，2012，33（5）：1-5.

[8]朱齐丹，于瑞亭，刘志林.欠驱动船舶全局K指数航迹跟踪的级联反步法[J].船舶工程，2012，34（1）：47-51.

[9]Ashrafiuon H，Muske K，McNinch L，et al.Sliding mode tracking control of surface vessels[J].IEEE Transactions on Industrial Electronics，2008，55（11）：4004-4012.

[10]廖煜雷，庄佳园，李晔，等.欠驱动无人艇轨迹跟踪的滑模控制方法[J].应用科技学报，2011，29（4）：428-434.

[11]Fossen T I.Guidance and control of ocean vehicles[M]. New York：Wiley，1994.

[12]Khalil H K.Nonlinear systems[M].3rd ed.New Jersey，USA：Prentice-Hall，2002.

WANG Yan,ZHU Qidan,LIU Zhilin,YANG Zhen

College of Automation,Harbin Engineering University,Harbin 150001,China

In order to realize tracking arbitrary specified trajectory,a motion planning method is presented.All the desired attitudes are obtained by combining cubic spline interpolation,ship dynamic model,and discrete expected dots.Meanwhile,in order to realize fast tracking trajectory of underactuated surface vessels,global exponential tracking control law is proposed.Trajectory tracking error dynamic equation consists of two cascade subsystems based on diffeomorphism transformation.Then global exponential tracking control law is designed by using backstepping for error subsystems.The results of simulation experiments indicate that the proposed controller can effectively track arbitrary specified curve trajectory.

underactuated surface vessel;motion planning;tracking control;backstepping;exponential stabilization

针对目前欠驱动船舶航迹跟踪控制难以实现跟踪任意可行航迹问题，提出一种运动规划方法。利用多项式拟合，并结合船舶动力学模型，通过离散期望点规划出操作性可实现的全部期望姿态。同时，为实现欠驱动船舶的航迹快速跟踪控制，提出一种全局指数航迹跟踪控制律。引入微分同胚变换，建立两个级联的子系统构成的航迹跟踪误差动态方程；基于反步法的设计原理，运用Lyapunov直接方法对变换后的误差系统设计了全局指数航迹跟踪控制律。仿真结果验证了所提出的全局指数航迹跟踪控制律能够有效实现跟踪任意可行航迹。

欠驱动船舶；运动规划；跟踪控制；反步；指数稳定

A

U664

10.3778/j.issn.1002-8331.1209-0043

WANG Yan,ZHU Qidan,LIU Zhilin,et al.Motion planning and global exponential trajectory tracing of underactuated surface vessels.Computer Engineering and Applications,2013,49（5）：18-22.

国家自然科学基金（No.50909026）；黑龙江省自然科学基金（No.F200916）；中央高校基本业务专项资金（No.HEUCFR1116）。

王岩（1984—），男，博士研究生，主要研究方向为智能控制理论与应用、船舶控制；朱齐丹（1965—），男，工学博士，教授，博士生导师，主要研究方向为机器人控制、智能控制等；刘志林（1977—），男，工学博士，讲师，主要研究方向为混杂系统、预测控制、船舶控制；杨震（1984—），女，博士研究生，主要研究方向为船舶运动姿态预报、智能优化理论与方法。E-mail：wangyan0406@hrbeu.edu.cn

2012-09-10

2012-10-26

1002-8331（2013）05-0018-05

CNKI出版日期：2012-11-06 http://www.cnki.net/kcms/detail/11.2127.TP.20121106.1628.005.html