对称逻辑度量次范整子空间及其性质

楼志刚，刘宏昭，胡明娣

1.西安理工大学 机械与精密仪器工程学院，西安 7100482.西安邮电大学 通信与信息工程学院，西安 710121

对称逻辑度量次范整子空间及其性质

楼志刚1，刘宏昭1，胡明娣2

1.西安理工大学 机械与精密仪器工程学院，西安 710048
2.西安邮电大学 通信与信息工程学院，西安 710121

1 引言

现实世界中的命题是多种多样的，其中有大量的具体命题是不能简单地用“真”和“伪”对其可信性作二值判断的，而应当对它们的可信性程度进行量化判断。正式基于这种考虑，王国俊教授将程度化思想引入到了数理逻辑之中，建立起了计量逻辑学的基本理论（参看文献[1-6]）。此后又与概率逻辑学相结合，将随机化思想引入到了经典的推理模式中（参看文献[7-8]）。如今已在包括Lukasiewicz，L*，Gödel，和Goguen等多种命题逻辑系统中构造出了相应的逻辑度量空间，从而将近似推理引入到了素以严格的形式化推理为特征的各种命题逻辑系统之中。值得注意的是，对于逻辑度量空间自身构造的研究已渐次开始被关注（参看文献[9-14]）。由于对于二值命题逻辑而言，逻辑公式的真度完全由其诱导的布尔函数所决定，而在密码学中已经对布尔函数有了非常深刻的研究（参看文献[15]），所以在文献[12]将密码学中对称布尔函数的概念引入到了二值计量逻辑学理论之中，定义了对称逻辑公式和准对称逻辑公式，讨论了对称公式集在经典逻辑度量空间中的分布。那么，又进一步思考，在经典逻辑度量空间中，能否构造出类似于Banach空间、Hilbert空间等一样的空间，能否在这样的空间中存在一些组合表示等。正是基于这些思考，在本文中引入最简对称逻辑公式，定义了逻辑公式的加法和数乘运算。证明了对称逻辑公式的全体关于所定义的加法和数乘构成线性次范整子空间，并且讨论了该子空间的一些简单性质。

2 基础知识

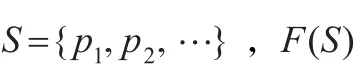
设{0，1}是最简单的布尔代数，其中：

﹁a=1-a，a⋁b=max{a,b}，a→b=1当且仅当a≤b（1）则{0，1}也是(﹁，⋁，→)型代数。

定义2.2[4]设A(p1,p2,…，pn)是含有原子公式p1,p2,…，pn的逻辑公式，用 xi取代 pi(i=1，2，…，n)，并按式（1）理解逻辑连接词﹁，⋁，→，则得一布尔函数 fA:{0，1}n→{0，1}，称为A所诱导的布尔函数。称 f-1(1)/2n为公式A的真度，记为τ(A)。设A，B为F(S)中的两个公式，称

为A与B之间的相似度。再令

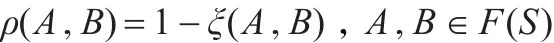
是F(S)上的伪距离，称(F(S)，ρ)为逻辑度量空间。

已知两个逻辑公式逻辑等价当且仅当它们之间的相似度为1，或等价地，它们之间的伪距离为0[4]。

注2.1公式A中的原子公式的标号未必是从1到n的连续编号，但设其中最大编号为n，令B=A⋁(p1⋀﹁p1)⋁…⋁(pn⋀﹁pn)，则B与A逻辑等价，B中原子公式的标号就是从1到n的连续编号了，所诱导的布尔函数也就可写为f(x1，x2，…，xn)的形式了。以下凡提到含有n个原子公式的逻辑公式A，恒假定A中的原子公式的标号是从1到F(S)的连续编号。

定义2.3逻辑等价关系≈是F(S)上的(﹁，→)型同余关系，商代数[F(S)]=F(S)/≈是布尔代数，称为Lindenbaum代数。以[A]记逻辑公式A所在的等价类，定义

则ρ*是[F(S)]上的距离函数，将ρ*简记为ρ，称M=([F(S)]，ρ)为经典逻辑度量空间。

3 经典逻辑度量次范整线性空间

定义3.1[11]令M(n)={[A]:A中含有的原子公式包含于{p1，p2，…，pn}}，则

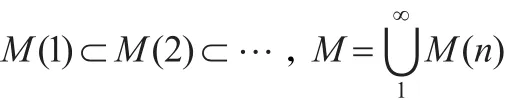
由注2.1容易得到上式成立，并且原子公式 pk∈M(n)当且仅当k≤n。

命题3.1[11]用 B(n)记全体n元布尔函数之集，那么，M(n)与 B(n)之间存在一一对应关系 (n=1，2，…)，且(M(n)，ρ)是经典逻辑度量空间M的有限的闭子空间。

注3.1任取[A]∈M(n)，则φ(A)是一个 n元布尔函数。将其自变量之集{0，1}n中的全体2n个n维向量按字典序从小到大排列为 β1，β2，…，β2n。设φ(A)(βk)=ck，则(c1，c2，…，c2n)是一个 2n维 0-1向量，记为Vec(A)。则φ(A)，[A]，Vec(A)完全相互唯一决定。

定义3.2[11]在{0，1}中规定加法⊕为模2加法，即，0⊕0=0，0⊕1=1⊕0=1，1⊕1=0。将⊕按点式方法作用于V(2n)中的向量的每个坐标，则得V(2n)上的模2加法运算，仍记为⊕，即

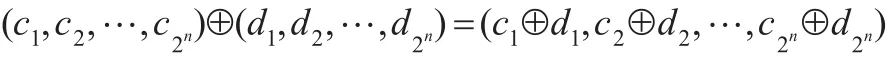
定义3.3[16]设(X,+,θ)是Abel群，Z是整数加群。如果

（1）对于每个序对(m，x)∈Z×X，X中有唯一的元mx与之对应，且满足：

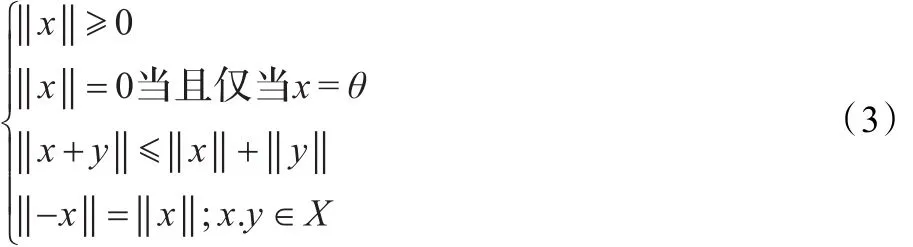
证明 设[A]、[B]是M(n)中的任意两个元，并且与之对应的Vec(A)=(a1，a2，…，a2n)，Vec(B)=(b1，b2，…，b2n)。

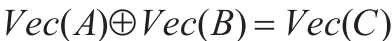
即

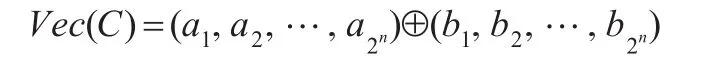
由上定义可见，M(n)中的加法满足交换律，结合律。

设m是任意整数，定义m[A]=[A]⊕[A]⊕…⊕[A]，m个[A]相加。则易证在M(n)中数乘满足：m[A]=若m是偶数，m[A]=[A]若m是奇数，m∈Z（4）由式（4）易证式（2）中的各等式对于 x，y∈M(n)和m，n∈Z都成立。

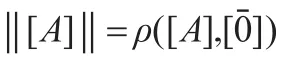
[A]+[B]=[C]当且仅当Vec(A)⊕Vec(B)=Vec(C)此时有：

这里 ρ是经典逻辑度量空间([F(S)]，ρ)的子空间M(n)中的度量函数。显然

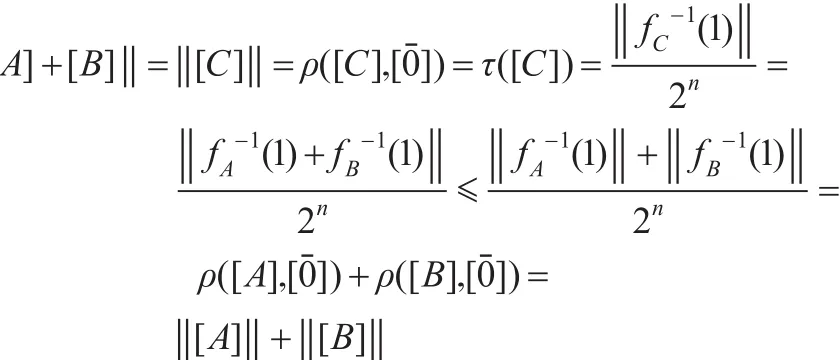
4 对称逻辑度量次范整线性空间S(n)

定义4.1[15]称映射 f:{0，1}n→{0，1}为n元布尔函数。设α=(x1，x2，…，xn)∈{0 ，1}n，若 f(α)=1，则称α为 f的特征向量；称α中1的个数为α的重量。若一旦{0 ，1}n中某重量为k的向量是 f的特征向量，那么{0 ，1}n中全部重量为k的向量都是 f的特征向量(0≤k≤n)，则称 f为对称的布尔函数。以下用N(f)记 f的特征向量的个数，显然：

注4.1上面关于 f对称性的表述并非文献[15]中的原始定义，但易证本文的定义和文献[15]中的定义是等价的。

定义4.2[15]称

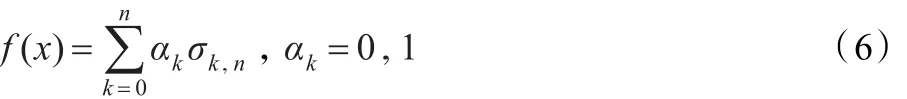
为n元对称布尔函数 f的基本表示形式，其中：

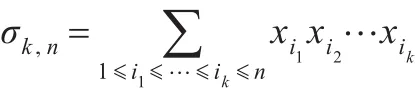
注4.2定义4.2中采用的是 f的多项式表示，由于不影响本文的推导，为节省篇幅起见，对什么是多项式表示不作介绍。

定义4.3[15]设A是含有n个原子公式的逻辑公式。如果A所诱导的布尔函数是对称布尔函数，则称A为n元对称逻辑公式。

命题 4.1[12]设 B(p1，p2，…，pm)与对称逻辑公式A(p1，p2，…，pn)逻辑等价，且 B(p1，p2，…，pm)不是对称逻辑公式，则n＜m。

命题4.2[12]设二对称逻辑公式 A(p1，p2，…，pm)与B(p1，p2，…，pn)逻辑等价，且A与B不是重言式，也不是矛盾式，则m=n。

由命题4.1，命题4.2容易得到：

注4.3令S(n)={[A]|A是n元对称逻辑公式}，那么S(1)⊆S(2)⊆…⊆S(n)⊆…不成立。例如：A=p1⋀p2∈S(2)，但是不属于S(k)，k≠2。

例4.2设Y=M(2)⊆M(n)（当 n＞2时），容易验证(M(2)，+，‖◦‖)满足定义4.4的条件，成为Z-子空间。同理，由定义3.1知中有很多个Z-子空间存在。

5 对称逻辑次范整线性空间的简单性质

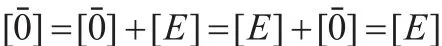
证明 设[A]是n元对称逻辑公式，假设[B]和[C]都是[A]的负元素，当且仅当满足：

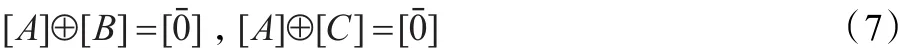
首先由文献[12]的论证可知[B]和[C]都是n元对称逻辑公式。其次，式（7）成立当且仅当：

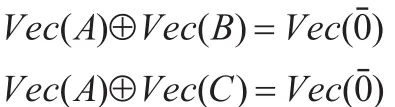
当且仅当对任意的α∈{0，1}n，有：

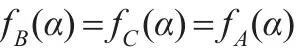
当且仅当：

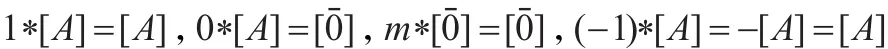
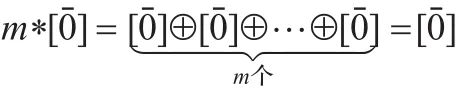
最后，因为1*[A]=[A]，

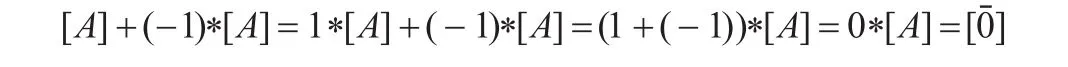
知：

(-1)*[A]=-[A]=[A]

6 结束语

本文继文献[11]利用平移群建立M(n)次范整线性空间和文献[12]引入对称逻辑公式并讨论了对称逻辑公式及在逻辑度量空间中的分布之后，给出M(n)次范整线性空间新的运算的定义，首次提出对称逻辑度量次范整线性子空间的概念，并讨论了它的简单性质。这样的讨论使得对逻辑度量空间内蕴结构的建立迈进了新的一步。当然，紧接着可以类似其他赋范空间一样，给出它的一组基，确定它的维数，探讨该空间中是否存在收敛的柯西序列等，这些结果于另文给出。

[1]王国俊.计量逻辑学（I）[J].工程数学学报，2006，23（2）：191-215.

[2]王国俊，宋建社.命题逻辑中的程度化方法[J].电子学报，2006，34（2）：252-257.

[3]王国俊，傅丽，宋建社.二值命题逻辑中命题的真度理论[J].中国科学：A辑，2001（11）：998-1008.

[4]王国俊.数理逻辑引论与归结原理[M].2版.北京：科学出版社，2006.

[5]WangG J，Zhou H J.Introductiontomathematical logic and resolution principle[M].Oxford，U.K：Alpha Science International Limited，2009.

[6]Wang G J，Zhou H J.Quantitative logic[J].Information Sciences，2009，179：226-247.

[7]王国俊，惠小静.概率逻辑学基本定理的推广[J].电子学报，2007，35（7）：1333-1340.

[8]惠小静，王国俊.经典推理模式的随机化研究及其应用[J].中国科学：E辑，2007，37（6）：801-812.

[9]Wang G J，She Y H.A topological characterization of consistency of logic theories in propositional logic[J].Mathematical Logic Quarterly，2006，52（5）：470-477.

[10]胡明娣，王国俊.经典逻辑度量空间中的反射变换[J].陕西师范大学学报：自然科学版，2009，37（6）：1-4.

[11]王国俊，胡明娣.经典逻辑度量空间中的模2次范整线性空间结构[J].电子学报，2011，39（4）：899-906.

[12]胡明娣，王国俊.对称逻辑公式在经典逻辑度量空间中的分布[J].电子学报，2011，39（2）：418-423.

[13]胡明娣，楼志刚.经典逻辑度量空间中的边角关系[J].西北大学学报：自然科学版，2011，41（2）：206-211.

[14]王庆平，王国俊.对称逻辑公式在L_3_逻辑度量空间中的分布[J].计算机学报，2011，34（1）：105-114.

[15]温巧燕，钮心忻，杨义先.现代密码学中的布尔函数[M].北京：科学出版社，2000.

[16]王国俊，王伟.经典逻辑度量空间[J].数学学报，2001，44（1）：159-168.

LOU Zhigang1,LIU Hongzhao1,HU Mingdi2

1.School of Mechanical and Precision Instrument Engineering,Xi'an University of Technology,Xi'an 710048,China
2.School of Telecommunication and Information Engineering,Xi'an University of Posts&Telecommunications,Xi'an 710121,China

Addition and number multiplication are defined in the classical logic metric space,and the norm are introduced by using the degree of the formulas.It is proved that the classical logic metric space builds a Z（2）-normable linear logic space.The concept of a Z（2）-normable linear logic sub-space is introduced,according to the definition,it is proved that the set of n-symmetric logical formula constitutes the a Z（2）-normable linear logic sub-space.Some basic characters of the sub-space are discussed.

symmetric Boolean function；symmetric logic formula;Z（2）-normable linear logic space;norm;symmetric logic Z（2）-normable linear sub-space;classical logic metric space

在经典逻辑度量空间中定义了加法和数乘运算，利用公式的距离引入了经典逻辑度量空间中的范数的概念，从而证明了经典逻辑度量空间作成线性次范整空间。引入了次范整线性子空间的概念。证明了n元逻辑公式之集中的对称逻辑公式子集构成了次范整线性子空间，并讨论了该子空间的简单性质。

对称布尔函数；对称逻辑公式；次范整线性空间；真度；对称逻辑子空间；经典逻辑度量空间

A

O159

10.3778/j.issn.1002-8331.1112-0131

LOU Zhigang,LIU Hongzhao,HU Mingdi.Classical symmetrical logic metric sub-space and its properties.Computer Engineering and Applications,2013,49（5）：40-43.

陕西省基金项目（No.102-00X903）。

楼志刚，男，在读博士研究生，讲师，主要研究领域为故障识别、数据分析、模糊控制；刘宏昭，男，教授，博士生导师，主要从事机电系统建模、测试及控制、机构学及CAD、机械动力学研究；胡明娣，女，副教授，主要研究方向为数理逻辑、模糊控制。

2011-12-08

2012-03-13

1002-8331（2013）05-0040-04

CNKI出版日期：2012-05-21 http://www.cnki.net/kcms/detail/11.2127.TP.20120521.1142.075.html