主被动传感器自适应量测融合算法

崔 波，张家树

西南交通大学 信息科学与技术学院，成都 610031

主被动传感器自适应量测融合算法

崔 波，张家树

西南交通大学 信息科学与技术学院，成都 610031

1 引言

主、被动传感器的量测数据融合问题已有了很多算法，如最近邻法、高斯和法、概率数据关联滤波法、全邻最优法、多模型算法、多元假设法、加权算法等，其中加权算法是最常使用的一种量测融合算法[1]。加权融合算法主要包括等加权算法和方差加权算法，都属于固定加权算法[2]。由于传感器测量误差由固定误差和随机误差两部分组成，固定测量误差由传感器设备本身特性决定，随机测量误差会受到传感器与运动目标间距离、自然或人为干扰的影响。在不考虑外界干扰的条件下，传感器与目标间的距离成为影响随机测量误差的主要原因[3-4]，其中主动传感器的随机测量误差受距离参数的影响尤为突出。当这部分随机误差已经大到影响整个系统的跟踪精度时，采用固定权重的主、被动传感器就不能满足要求[5]。本文针对影响随机测量误差的距离参数进行讨论，提出了基于模糊距离阈值的主被动传感器变权重量测融合算法，使用指数函数和模糊处理技术实时表示量测融合过程中传感器权重的变化。

2 融合跟踪模式选择

假设主、被动传感器位于同一个观测平台上，设置两个距离阈值r0和rt，r0表示主动传感器有效探测距离，rt表示主动传感器可以探测到目标的距离极限。当运动目标和观测平台间的距离小于r0时，由于主动传感器的测量精度远远高于被动传感器的测量精度，单纯的主动传感器的跟踪性能已经能够满足系统要求，只需采用主动传感器跟踪就可以了。

当运动目标和观测平台间的距离位于区间(r0,rt)时，表示主动传感器可以探测到目标，但运动目标已经超出主动传感器有效探测距离。目标距离观测平台越远，由于距离因素引起的主动传感器的随机误差就越大，主动传感器的测量精度就随之快速下降。这一部分随机误差不能被简单地忽略掉，纯粹的主动传感器已经不能满足跟踪系统的要求，所以要引入被动传感器，采用主、被动融合跟踪模式。

当目标和观测平台间的距离大于rt时，表示主动传感器已经探测不到目标。被动传感器由于作用范围广仍然可以探测到目标，所以采用被动传感器进行跟踪，此时为纯被动跟踪模式。

3 主被动传感器自适应量测融合算法

部署在同一个观测平台上的主、被动传感器跟踪同一个运动目标，假设已完成坐标转换和数据关联步骤。将时间对准后的测量数据基于距离阈值进行权重计算并对权重进行模糊处理，然后进行量测融合，最后跟踪滤波。

3.1 时间对准

由于主动传感器和被动传感器对目标的量测是独立进行的，采用不同的测量技术，采样周期也各不相同，测量数据到达融合中心的时间延迟也存在着差异，导致主、被动传感器的测量数据不同步，在数据融合之前先要将不同步的量测数据进行时间对准到同一融合时刻。假设被动传感器相邻的两个采样时间点分别是t1p和t2p，对应的主动传感器的采样时间点是ta，并且满足条件t1a≤ta≤t2p。时间对准的一般做法是将各传感器的量测数据统一到扫描周期较长的其中一个传感器上，这里将主动传感器的采样时间作为时间基准，即t=ta。本文中采用了常用线性插值时间对准方法，对被动传感器的测量数据在时间t处进行预测，使之与主动传感器的量测数据在时间上对齐。采用线性插值法时间对准后的观测值如式（1）所示[6]。这里Za是主动传感器在时间ta的估计状态，Z1p是被动传感器在时间t1p的测量值，Z2p是被动传感器在时间t2p的测量值，Zfa是主动传感器在时间对准后的估计值，Zfp是被动传感器在时间对准后的估计值。

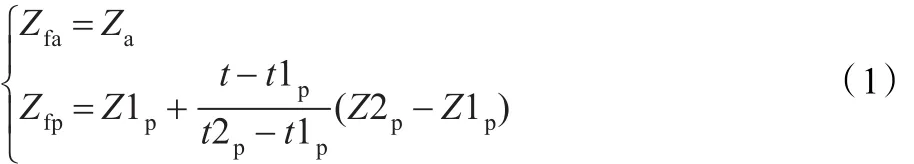
3.2 基于距离阈值的权重计算

将时间对准后的Zfa和Zfp基于距离阈值进行权重计算。

对于纯主动跟踪模式，设置主动传感器在量测融合时所占权重为1，被动传感器在量测融合时所占权重为0。

对于主、被动融合跟踪模式。根据k时刻的估计位置自适应的调整主、被动传感器在数据融合时所占的权重。主动传感器在数据融合时所占的权重随着目标距离的增大而减小，即成减函数关系，并且主动传感器权重减小的速度很快，采用指数方式表示这种快速下降关系。

对于纯被动跟踪模式，被动传感器在量测融合时所占权重为1，主动传感器在数据融合时所占权重为0。

根据以上分析，主动传感器在数据融合时，所占的权重k为[7]：

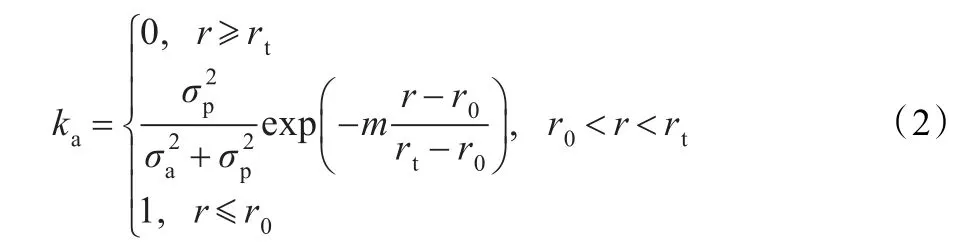
3.3 权重模糊处理

在实际的跟踪过程中，对于主动传感器来说，有效监控距离和监控距离极限是存在模糊性的。对于距离监控极限rt还好，目标远离观测平台直到越过监控距离极限rt的过程中，主动传感器在数据融合中所占的权重逐渐接近0，不存在权重的突变。但对于有效监控距离r0来说，主动传感器在r0处是存在模糊性的，简单的设置阈值会引起权重的突变，所以要采用模糊处理技术。这里采用椭圆曲线来处理这种模糊性，给出三个阈值r0，rm和rt(r0＜rm＜rt)，则主被动传感器在数据融合过程中各自所占的权重为[8-9]：

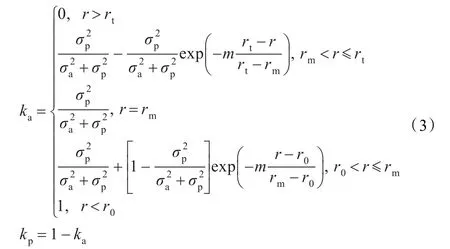
3.4 主被动传感器量测融合

基于模糊距离阈值的主、被动传感器量测融合结果为：

其中ka是主动传感器在数据融合时所占权重，kp是被动传感器在数据融合时所占权重。Zfa是主动传感器在时间对准后的估计值，Zfp是被动传感器在时间对准后的估计值。

3.5 滤波跟踪

将量测融合后的结果Zf作为卡尔曼滤波器的最新观测数据进行跟踪滤波。

则k时刻预测状态为：

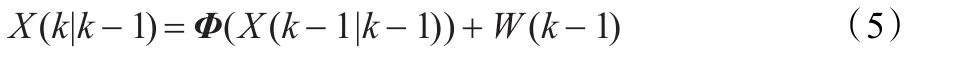
预测协方差：

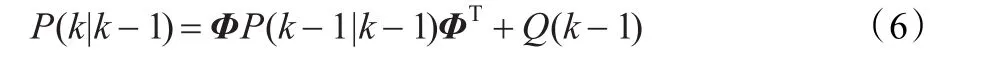
Kalman增益：

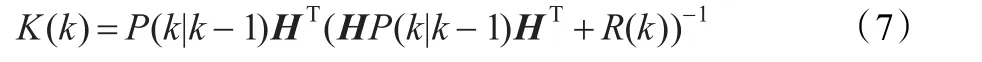
滤波方程：

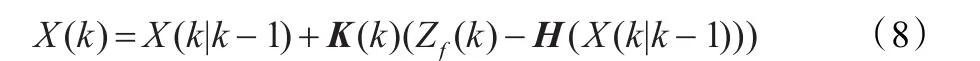
滤波协方差：

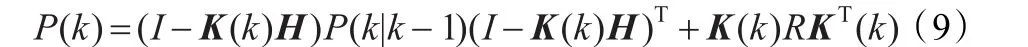
则式（7）中的X(k)是k时刻运动目标的估计状态。

4 仿真结果及分析

位于地面的同一观测平台上部署着主动雷达和被动传感器。为简单起见，采用二维空间的主、被动传感器目标跟踪方式。设置运动目标的初始位置坐标为（100，150）（单位：km）。对于主动雷达来说，有效的监控距离是200 km，测量方差是0.3 km，采样时间是0.1 s。当目标与观测站间的距离超过主动雷达的有效监控距离200 km时，主动雷达的测量误差大大增加，并且距离越远，测量误差越大；当目标与观测站间的距离超过300 km时，主动雷达已经不能锁定目标了。对于被动传感器来说，有效的监控距离是500 km，测量方差是1.2 km，采样时间0.05 s。在仿真实验中，运动目标做远离观测平台的曲线运动。图1给出了纯主动雷达、纯被动传感器、基于距离阈值的主、被动传感器量测融合的跟踪轨迹。

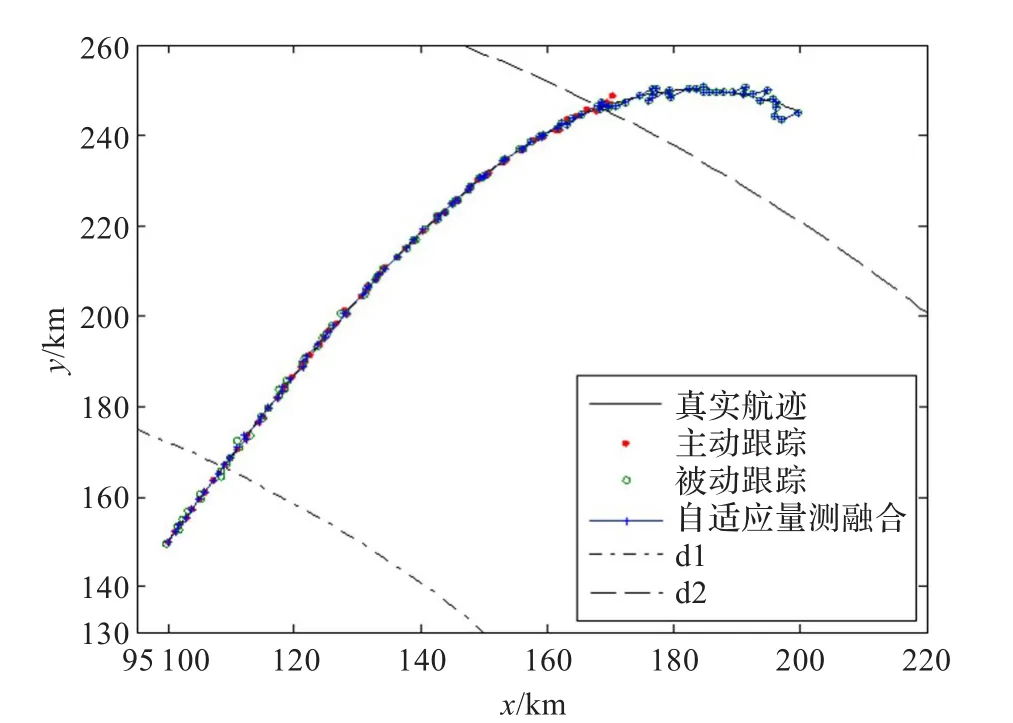
图1 三种跟踪模式估计航迹对比

图2给出了主、被动传感器随距离参数变化的权重变化，x轴表示运动目标和观测平台间的距离，y轴表示对应的传感器在数据融合时所占的权重。图2（a）表示随着目标和观测平台间的距离增大主动传感器权重变化过程，图2（b）表示随着距离增加被动传感器的权重变化过程。图3给出了基于模糊距离阈值主、被动传感器随距离参数变化的权重变化过程。从仿真结果中可以看出当目标和观测平台间的距离小于主动传感器的有效监控距离r0时，主动传感器的测量数据在融合时所在的权重为1，被动传感器的测量数据在融合时所在的权重为0，即被动传感器不参与数据融合，采用纯主动跟踪模式；目标和观测平台间的距离位于主动传感器的有效监控距离和极限监控距离之间即区间(r0,rt)时，采用主被动融合跟踪模式，随着距离的增加，主动传感器因测量误差快速增加，其测量数据在融合时所占的权重迅速下降，并且下降速度极快，呈指数型下降趋势，而被动传感器测量数据在融合时所占的权重迅速上升；当目标和观测平台间的距离超出主动传感器的距离监控极限rt时，主动传感器因其不能测量到目标，退出了对运动目标的跟踪，故采用纯被动跟踪模式，主动传感器的测量数据在融合时所在的权重为0，被动传感器在数据融合时所占权重为1。

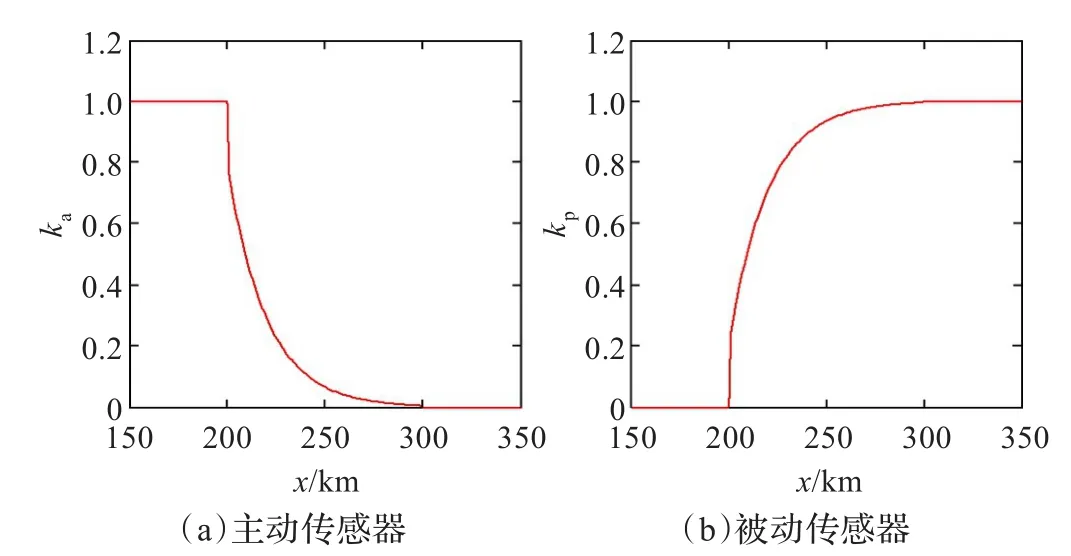
图2 基于距离阈值的传感器权重变化

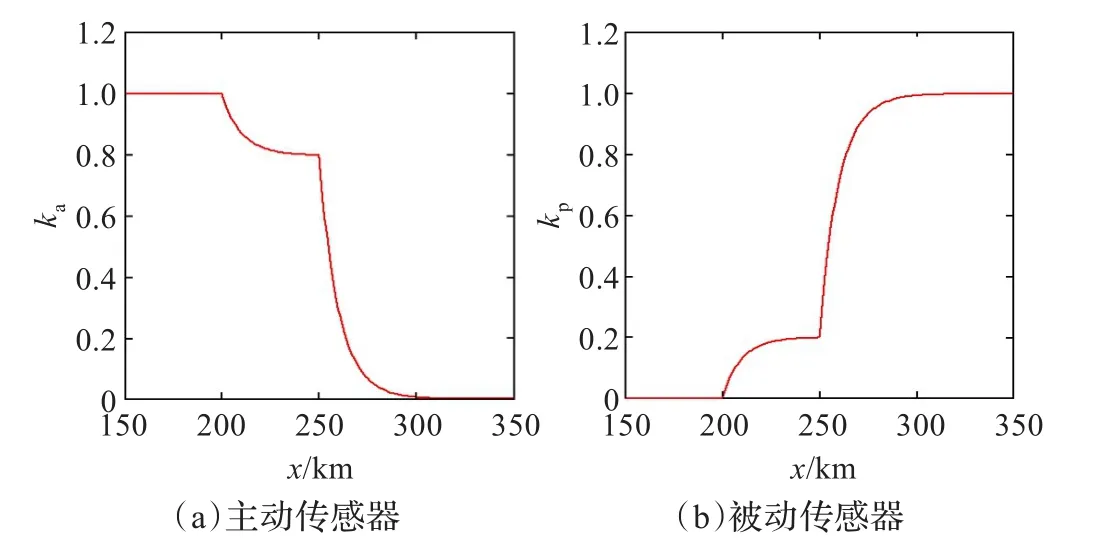
图3 基于模糊距离阈值的传感器权重变化

图4给出了纯主动雷达、纯被动传感器、主被动传感器量测融合的均方根误差对比关系图。从图中可以看出，整个跟踪过程被动传感器的均方根误差基本保持平稳，主动传感器的均方根误差变化较大，这是因为主动雷达受距离参数影响随机误差变化较大的原因。当被跟踪目标位于主动传感器的有效监控范围内（200 km）时，主动传感器受距离参数影响的随机误差很小，和主动雷达本身的固定误差比较起来可以忽略不计，并且主动雷达的测量精度要远远高于被动传感器的测量精度，所以主动雷达的距离均方根误差是最小的，要远远小于纯被动跟踪模式的距离均方根误差，融合算法此时将主动雷达的测量数据作为最后的融合结果；当运动目标超出主动传感器的有效监控范围内（200 km），但主动传感器仍能监控到目标时，即没有超出主动雷达的监控极限（500 km）时，可以看出主动传感器的距离均方根误差不断增加，量测数据的可信度逐渐下降，此时引入被动传感器，并且随着目标的运动实时调整主、被动传感器在数据融合过程中所占的权重，在此过程中，无法确定到底哪一个传感器的量测数据具有更高的可信度，但是知道每个传感器的权重变化趋势，采用这种实时变权重的方法，可以增加跟踪系统稳定性，避免估计结果强烈偏离目标真实运动状态的情况发生；当主动传感器已经不能监控到目标，由于距离过远造成主动传感器的测量误差过大，主动传感器退出跟踪过程，由被动传感器进行跟踪，完成了监控权的转换。

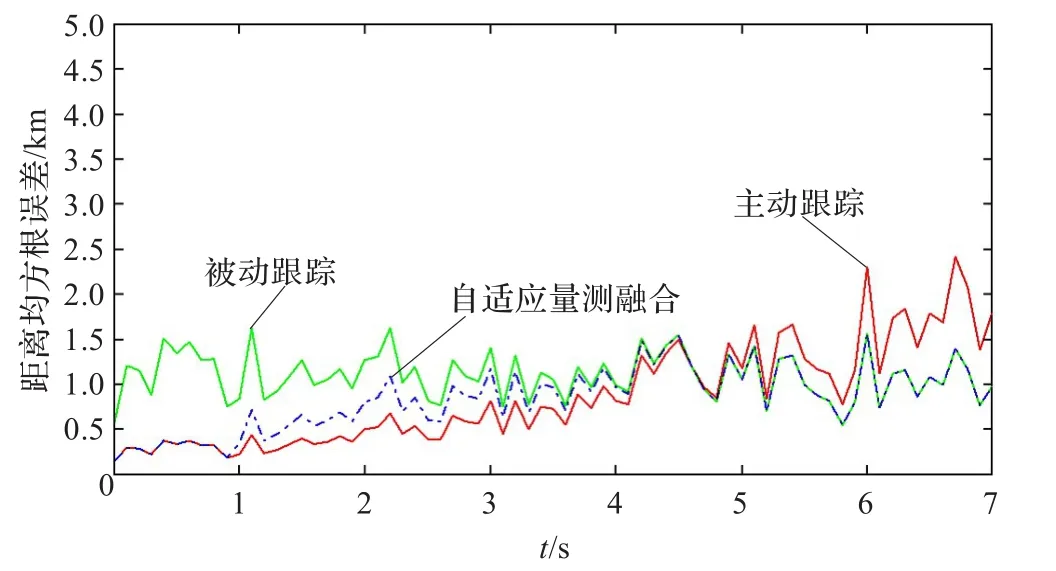
图4 三种跟踪模式均方根误差对比

图5给出了固定权重和基于距离阈值变权重融合算法均方根误差对比图。从图中可以看出，在跟踪开始时由于运动目标和观测平台间的距离较近，由距离参数引起的随机误差影响不大，此时主要存在的是传感器本身的固定误差，因此固定权重和变权重融合方法的跟踪精度相差不大；当运动目标逐渐远离观测平台，距离参数引起的主动传感器的随机误差逐渐增大，但还没有超过主动传感器本身的固定误差的影响，主动传感器的测量精度仍然高于被动传感器，此时采用固定权重数据融合算法的跟踪精度要略好于基于距离阈值的变权重数据融合算法；当距离参数引起的主动传感器的随机误差已经足够大，主动传感器的测量精度和被动传感器的测量精度相当，此时采用变权重数据融合算法要好一些；当主动传感器已经无法监控到运动目标时，就采用纯被动传感器进行跟踪了。总的来说，整个跟踪过程中基于距离阈值变权重融合算法的均方根误差基本保持平稳，固定权重融合方法随着目标的机动均方根误差变化较大。从跟踪系统的稳定性和总体跟踪精度来说，基于距离阈值的变权重数据融合算法的跟踪性能要好于固定权重融合方法。

图5 固定权重和自适应量测融合算法均方根误差对比

5 结束语

传感器由于自身或外界干扰的情况下不能全程参与工作，本文考虑影响传感器随机测量误差的距离因素，提出了一种基于模糊距离阈值的主、被动传感器变权重量测融合算法，分析了传感器跟踪模式的选择依据，利用指数函数和模糊处理技术实时改变主被动传感器在量测融合过程中所占的权重，充分利用了主、被动传感器在测量上的互补特性，提高系统的跟踪精度，也为跟踪传感器对目标监控权的转换提供了一定的依据。

[1]杨国胜，窦丽华.数据融合及其应用[M].北京：兵器工业出版社，2004：114-120.

[2]曲润峰.主/被动雷达信息融合方法研究与应用[D].西安：西北工业大学，2005：30-36.

[3]计征宇，皮亦鸣.TVM制导中数据融合的一种新算法[J].雷达科学与技术，2006，4（2）：93-103.

[4]王德纯，丁家会，程望东.精密跟踪测量雷达技术[M].北京：电子工业出版社，2006.

[5]陈永光，李修和，沈阳.组网雷达作战能力分析与评估[M].北京：国防工业出版社，2006.

[6]潘宁，张林让.主被动雷达数据融合及跟踪[J].雷达科学与技术，2008，6（1）：61-64.

[7]丁兴俊，周德云，胡昌华，等.基于主/被动雷达双传感器的自适应跟踪融合算法[J].西北工业大学学报，2006，24（2）：190-194.

[8]刘源.基于模糊信息处理的数据融合方法研究[D].西安：西安电子科技大学，1999：13-14.

[9]Cui Bo，Zhang Jiashu，Yang Yu.Variable-weight data fusion from active and passive radars for target tracking[C]//2nd InternationalWorkshop on ComputerScience and Engineering. Chengdu：[s.n.]，2009：342-344.

CUI Bo,ZHANG Jiashu

School of Information Science&Technique,Southwest Jiaotong University,Chengdu 610031,China

To the influence of distance between observation station and target on tracking performance,a measurement fusion algorithm based on fuzzy distance threshold for active and passive sensors is introduced to the target tracking system.The method choosing data fusion module based on distance parameter is discussed,and exponential functions and fuzzy processing are used to compute real-time weight of each sensor in measurement fusion process through priori knowledge.Simulation shows that the adaptive measurement fusion algorithm is more stable and can bring all complementary characteristic into full play of active and passive sensors compared to traditional invariable-weight method when random errors caused by target distance cannot be ignored.

measurement fusion;distance threshold;active and passive sensors;fuzzy processing;variable-weight

针对观测平台和运动对象间的距离参数会对传感器随机测量误差带来影响的问题，提出了一种基于模糊距离阈值的主被动传感器量测融合算法。讨论了根据距离参数选择主被动融合跟踪模式的方法，采用指数函数和模糊处理技术，利用已有信息实时改变主、被动传感器在量测融合过程中所占的权重。仿真结果表明，当传感器和运动对象间的距离对随机测量误差的影响不能忽略时，基于模糊距离阈值的主被动传感器变权重融合算法和传统的固定权重融合算法相比更加稳定，能够充分发挥主、被动传感器间的互补特性。

量测融合；距离阈值；主被动传感器；模糊处理；变权重

A

TP212

10.3778/j.issn.1002-8331.1207-0307

CUI Bo,ZHANG Jiashu.Adaptive measurement fusion algorithm for active and passive sensors.Computer Engineering and Applications,2013,49（5）：23-26.

国家自然科学基金（No.60971104）；西南交通大学百人计划项目（No.SWJTU11BR179）。

崔波（1979—），女，在读博士，讲师，研究领域为数据融合、目标跟踪；张家树（1965—），男，博士研究生导师，教授，研究方向为信号与信息处理。E-mail：bcui@swjtu.edu.cn

2012-07-23

2012-10-22

1002-8331（2013）05-0023-04

CNKI出版日期：2012-11-02 http://www.cnki.net/kcms/detail/11.2127.TP.20121102.0914.004.html