基于遗传算法的动态出租车合乘模型研究

程 杰 唐智慧 刘 杰 钟 流

（西南交通大学交通运输与物流学院1） 成都 610031） （重庆公共运输职业学院轨道交通工程系2） 重庆 402247）

0 引 言

随着我国国民经济的高速发展和城市化进程的加快，机动车保有量持续增加，交通需求迅猛增长，交通拥堵日益严重.出租车作为城市交通的有机组成部分，由于价格偏高等原因，在非高峰时期经常处于空载状态；在高峰期又常因为大量出租车只载一位乘客而出现打车难的问题，因此推广有效的出租车合乘模式，可以提高出租车的运输效率，降低出租车空载率，协助城市公交缓解城市交通压力.

出租车合乘问题与DARP问题同属于乘客交通工具配对问题，在以往的DARP问题中，Teodorovic等［1－2］对动态 DARP问题和静态 DARP问题进行了区分，他们指出动态DARP问题是出现在路网中每个结点上的需求的时间和位置是随时间动态变化的，而静态DARP问题的需求是固定不变的.Coslovich 等［3－5］求 解 了 带 时 间窗的动态DARP问题.出租车合乘问题作为一个NP问题吸引了大量国内外学者的研究，Tao Chichung等［6］用贪婪算法对出租车合乘一对多模式和多对一模式进行了求解.Yan Shangyao等［7］将具有相同需求的乘客视作一个乘客组，然后出于安全与舒适的考虑，把出租车合乘问题中的乘客和出租车进行了分类，并借助时空网络图对问题予以描述.覃运梅等［8］采用固定费率对静态出租车合乘问题进行了求解.

本文重点研究不同类型出租车和不同类型乘客组的多对多模式的动态出租车合乘问题.综合考虑出行者与驾驶员的利益，对时间窗约束引入协调机制，建立了动态出租车合乘模型，并且针对模型特点采用了遗传算法进行求解.

1 问题描述

出租车动态合乘问题是乘客和出租车的匹配问题.在一固定时间（一般指系统刷新时间间隔）内，新的乘客组出现在不同的乘车点的情况是随机的且出租车的位置是随时间动态变化的.每一个乘客组属性包括：乘客组数量、起始点位置、出发和旅行时间窗约束以及乘客组类别.根据这些属性对该区域网络内一定数量出租车合理指派，组织乘客组间的合乘，利用优化模型确定每辆出租车合乘路径及所载各乘客组的乘车费率.动态出租车合乘问题的关键在于根据当前区域网络中乘客组和出租车状态，实时优化安排合乘方案.整个合乘过程用时空网络图描述见图1.

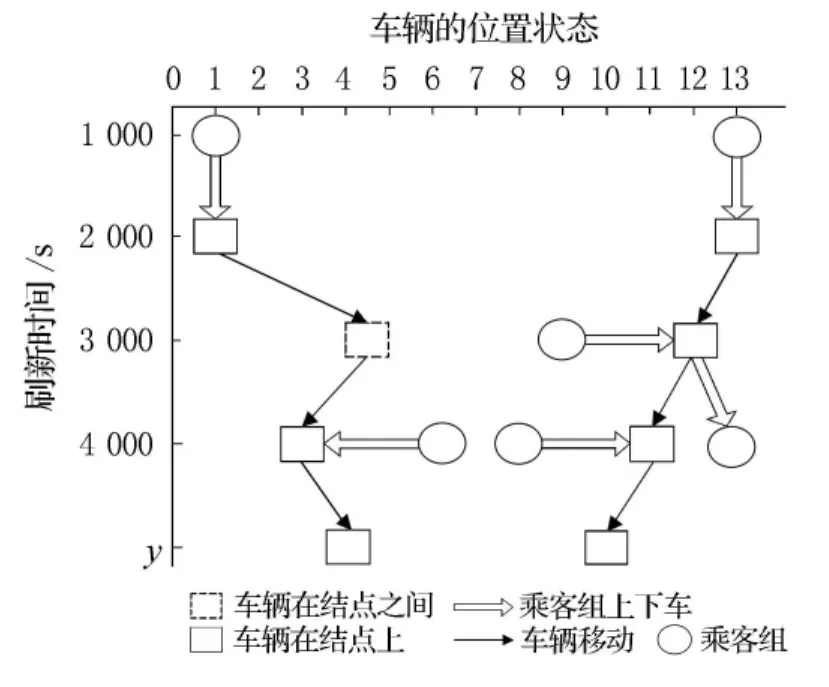
图1 动态出租车合乘的时空网络图

2 模型的建立

2.1 模型假设

在确定最优合乘方案时，当前网络的拥堵状况会对合乘方案产生影响，但这会使问题研究的复杂度增加，因此本文对问题给出如下前提假设：（1）所有乘客组时间窗约束均为软约束；（2）由于乘客组起讫点位置的随机性，允许车辆的逆向行驶；（3）不考虑网络的路径阻抗影响，每辆出租车的行驶相互独立；（4）所有乘客组的乘车需求都必须全部满足；（5）乘客组在合乘过程中不允许换乘；（6）不考虑出租车的燃料成本.

2.2 变量说明

K为所有车辆集合；H为网络节点集合；T为刷新时间；Pm为第m次刷新时刻所有车辆位置集合为第m次刷新时刻已经上车的乘客组集合为第m次刷新时刻没有上车的乘客组集合；Gm为第m次刷新时刻所有需求点乘客组状态集合为第K辆车经过的路径；为第g组乘客非合乘状态下从u到v所需的费用；FSm为在m次刷新时间所有车辆种类集合fsm∈FSm；PSm为在m次刷新时间所有乘客组种类集合psm∈PSm为车辆从i到j的运行时间；qg为第g组乘客的数量为uv之间最短距离为第g组乘客希望从u点出发的时间为第g组乘客希望到达v的时间为第k辆车抵达u的时间为第k辆车从u到v实际运行时间为u点上车v点下车的第g组乘客的合乘费率；r0出租车单位距离价格；C0为出租车起步价；L0为出租车起步距离为第k辆车从u出发时的载客量；C为出租车的最大容量；为u点上下车的乘客人数净差.

2.3 数学模型

2.4 决策变量

路径变量.设为路径变量，为1时，表示第k辆车经过边（i－j）；为0时，表示不经过.费用变量.设为费用决策变量，表示u点上车v点下车第g组乘客的合成费率.

2.5 目标函数和约束条件

目标函数第一部分为出行成本，第二部分为乘客费用.约束条件约束条件（2），（3），（7），（8）分别为司机收益、费率、出租车容量和决策变量约束，文献［9］已经对目标函数（1）和约束条件（2），（3），（7），（8）做了详细说明，本文不重复介绍.在动态合乘的过程中，乘客组分为两类集合：一类是已经上车的乘客组；另一类则是没有上车的乘客组.在刷新时间间隔内，车辆按照前一次的合乘方案路径行驶，在此期间有的乘客组已经上车处于前往目的地的途中，有的乘客组还未上车，同时也有新的乘客组需求产生.约束（4），（5）分别表示车辆外乘客组的运行和出发时间窗约束.因为在车内但未到达目的地的乘客组会对模型下次刷新时间点上求解的车辆路径结果产生影响，如果不考虑车辆内乘客组的限制，则可能导致车辆内乘客组无法在运行时间窗内到达目的地，所以随着车辆的运动，约束条件（6）表示车辆内乘客组运行时间窗约束的变化.约束（9）表示出租车和乘客组种类匹配，本文将出租车分为：1，一般型；2，只搭乘女性乘客型.乘客组按其人员构成分为4类：（1）全为男性；（2）全为女性但无性别要求；（3）全为女性但有性别要求；（4）男女混合.出租车种类为1时，只能与乘客组种类中1，2，4匹配，不能和种类3匹配.出租车种类为2时，只能与乘客组种类中2，3匹配，不能和种类1，4匹配.

3 模型求解算法

由于出租车合乘问题是一个NP问题，采用启发式算法容易编程求解.本文采用遗传算法求解该模型.本文所有乘客组时间窗约束均为软约束，即在无法满足该时间窗约束导致模型没有可行解时，乘客组接受协调机制，将其出发或达到时间窗约束适当增大［10］.除此之外，种类约束也接受协调机制.

3.1 变量编码

染色体采用实数编码的方式，染色体分为3部分，第一部分表示路径变量，第二部分为乘客组变量，第三部分为费率变量.除了第三部分外，其余都会用0将不同车辆的路径和乘客组隔开且乘客组的排列是按其搭乘车辆的顺序进行排序的.这样就可以直接从染色体中看出乘客组搭乘、费率及车辆合乘路径情况.例如染色体0 1 2 3 0 6 7 8 9 0 1 4 5 0 7 0 0.2 0.5 0.3 0.1表示第一辆车载有编号分别为1，4，5的乘客组，其合乘行驶路径为1―2―3，乘客组费率分别为0.2，0.5，0.3.第二辆车载有编号为7的乘客组，其行驶路径为6―7―8―9，乘客组7的费率为0.1.

3.2 适应度函数和选择算子

因为模型目标函数是求最小值，因此将染色体目标函数的倒数作为其适应度函数.模型带有约束条件，本文采用惩罚函数法对模型约束条件进行处理，将惩罚函数加在适应度函数上，如果某一染色体解满足约束条件，则它解码适应度函数会很小，从而在选择时被选中概率会小，遗传到下一代可能性变小.将种群中适应度值排名前1／4的染色体复制1次，中间2／4的染色体复制一次，抛弃最后1／4的染色体作为选择操作.

3.3 交叉算子

由于乘客组与费率问题的条件约束，如果仍使用简单交叉算子，将有可能产生大量的不可行解.因此本文对乘客组和费率分别进行交叉操作.采用文献［11］的交叉算子对乘客组部分进行交叉操作.对费率部分采用算术交叉.

3.4 变异算子

本文变异的策略是随机交换乘客组部分中2个等位基因，其乘客组对应的费率也相应的进行交换，根据文献［11］对变异后染色存在连续0的情况进行处理.整个动态出租车合乘流程图见图2.

图2 动态出租车合乘流程图

4 算例分析

算例路网如图3所示.设定现在网络中存在着30个出行需求点对，节点代表出租搭乘点，边的权值表示行驶距离，单位：km.路网中有5辆出租车，初始位置分别为节点7，2，25，10，30.根据成都市当前出租车的价格，本文规定出租车的起步价为8元，起步距离为2km，起步距离之后是1.9元／km，出租车运行速度为40km／h，每辆出租车最多载4位乘客.设置初始交叉概率为0.8，变异概率为0.1.

图3 算例网络

由于篇幅原因，本文只进行两次刷新计算，刷新时间间隔为1 000s，即调用模型2次.2次刷新时刻的乘客组信息分别见表1、表2.

表1 第1次刷新时刻乘客组信息

表2 第2次刷新时刻乘客组信息

利用Matlab编程计算，模型收敛性见图4.因为初始乘客组信息是随机给定，因此可能导致无可行解，本文引入协调机制，使得协调各乘客组的乘客组属性后，适应度函数值会增大，但这样可以得模型的可行解，最终得到较满意解.计算得到每辆出租车的行驶路径如下：出租车1：7─13─12─11─10─9─1；出租车2：19─11─12─14─22─24─17；出租车3：25─19─11─12─9─13─7─6─8─4─5；出租车4：10─2─1─6─7─14─21─22─30─29；出租车5：30─28─24─16─8─4.

图4 算法的收敛性

每个乘客组合乘与非合乘所交纳的费用见表3.从表中不难看出，合乘费用比非合乘费用少.另一方面，司机的收益也是本文研究的重点，在行驶同样距离的情况下，合乘时的司机收益比非合乘时大，5辆出租车在2次刷新时间的平均空载率分别为0.14，0.41，0.18，0.36，0，其中只有一辆出租车的空载率大于国内出租车平均空载率0.40即该辆出租车利用效率较低［12］.

表3 合乘前后费用与距离对比

表4 合乘前后司机收益与平均空载率

5 结 论

研究了动态出租车合乘问题，考虑了在乘客组、出租车分类型情况下，引入协调机制，建立了多对多模式的动态出租车合乘模型，并且在一个小型网络上进行了仿真测试，结果表明：出租车合乘减少了乘客费用，增加了司机的收益，同时空载率下降.尚未考虑出租车在合乘状态下的燃油成本和其他成本，这些还有待进一步研究.

［1］TEODOROVIC D，RADIVOJEVIC G.Fuzzy logic approach to dynamic dial－a－ride problem［J］.Fuzzy Sets and Systems，2000，116（2）：23－33.

［2］COLORNI A，RIGHINI G.Modeling and optimizing dynamic dial－a－ride problems ［J］.International Transactions in Operational Research，2001，8（3）：155－166.

［3］COSLOVICH L，PESENTI R，UKOVICH W.A twophase insertion technique of unexpected customers for a dynamic dial－a－ride problem ［J］.European Journal of Operational Research，2006，175（2）：1605－1615.

［4］DIANA M，DESSOUKY M.A new regret insertion heuristic for solving large－scale dial－a－ride problems with time windows［J］.Transportation Research Part B，2004，38（4）：539－557.

［5］FU L.Scheduling dial－a－ride paratransit under timevarying stochastic congestion［J］.Transportation Research PartB，2002 36（2）：485－506.

［6］TAO Chichung，CHEN Chunying.Dynamic rideshare matching algorithms for the taxipooling service based on intelligent transportation system technologies［C］／／2007International Conference on Management Science and Engineering，Harbin，China，2007：399－404.

［7］YAN Shangyao，CHEN Chunying，WU Chuanche.Solution methods for the taxi pooling problem［J］.Transportation，2011，39（3）：723－748.

［8］覃运梅，石 琴.出租车合乘模式的探讨［J］.合肥工业大学学报，2006，29（1）：77－79.

［9］周和平，钟璧樯.出租车合乘路径选择与费率优化模型［J］.长沙理工大学学报，2011，8（1）：20－25.

［10］JORGENSEN R M，LARSEN J，BERGVINSDOTTIR K B.Solving the dial－a－ride problem using genetic algorithms［J］.Journal of the Operational Research Society，2007，58（4）：1321－1331.

［11］唐 坤.车辆路径问题中的遗传算法设计［J］.东华大学学报，2002，28（1）：66－70.

［12］刘鸿婷.出租车运力规模评价与优化研究［D］.大连：大连海事大学，2011.