空中机动平台光电吊舱对目标定位方法分析*
黄 亮 张建强 刘 忠
(海军工程大学电子工程学院 武汉 430033)
0 引 言
光电跟踪探测系统以其被动隐蔽、不受电磁干扰、精度高等优点而成为现代军事警戒探测系统的重要手段之一.但由于目标辐射在地球表面的传播特性、地球曲率半径以及光传播的直线性等因素的影响,使岸基和舰载光电跟踪探测系统的作用距离受到了限制,从而制约了光电装备潜能的充分发挥.
受到星载光电系统的启发,20世纪80年代中期以来,世界各国纷纷发展各类基于空中机动平台的光电系统,例如预警机的远程预警吊舱、直升机的反潜吊舱等.光电吊舱的出现弥补了上述光电探测系统的不足,给光电跟踪和探测技术开辟了一个新的应用领域[1].
光电吊舱可精确测量地面目标或空间目标相对空中平台的方位角和俯仰角,再结合空中平台的GPS位置信息,就可以实现对目标运动参数的解算.在此应用背景下,传统的对目标定位的三角几何定位方法,虽然算法简单、易于实现,但定位精度不高,而且只能定位海面目标.文献[2]提出了用正弦定理的几何关系测距、然后对目标定位的原理,由于是用物理的单站来实现体制上的虚拟多站,所以只能跟踪海面慢速目标.文献[3-4]利用时差定位方法分析了机载雷达对超视距目标定位的情形,但需测得雷达对目标的径向距离,而且是在多观测站情况下定位,布置复杂,不易实施.文献[5]使用测向交叉定位算法,却仅针对二维条件下.此外,可应用卡尔曼滤波及其拓展滤波(如 EKF,UKF 等)[6-9]分析目标运动,但需初始化系统的动态特性,若参数选择不当,将严重影响定位精度.
因此,针对单个空中机动观测平台对目标定位的情形,本文首先分析了传统的三角几何定位方法的不足,并提出了一种基于最小二乘的目标运动分析方法,可以实现对海上及陆上目标的高精度跟踪定位,从而避免了上述各种方法的不足.
1 光电吊舱测角模型
空中机动平台中光电吊舱的角度测量值包括2个:(1)光轴指向(吊舱质心与目标连线)与基准纵轴(正北方向)的夹角,称为方位角β;(2)光轴指向与基准面(水平面)的夹角,即为俯仰角ε,见图1.
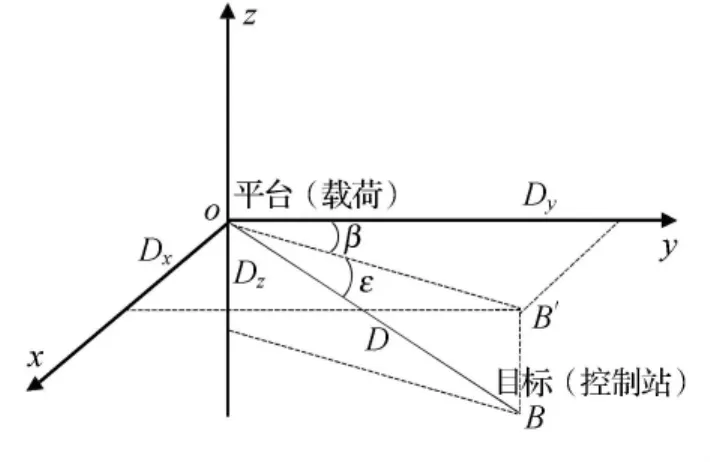
图1 光电吊舱的测角原理
2 三角几何定位模型及误差分析
这种方法基于空间几何原理,利用三角形角边关系确定目标位置及运动参数.这也是目前工程领域内存在的一种简单实用的定位方法.
根据俯仰角ε的定义,有
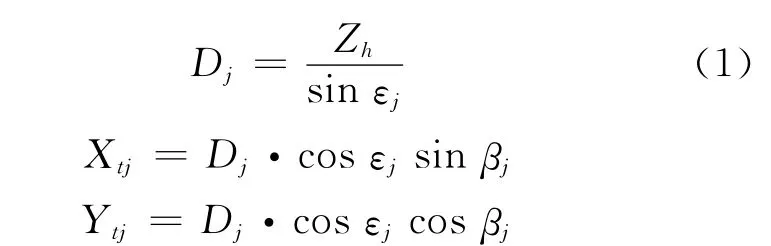
从而可以求得目标的速度分量
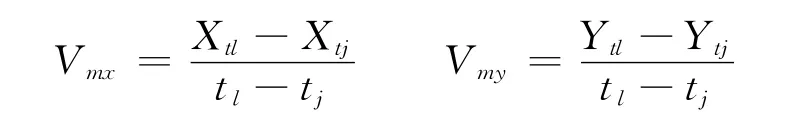
所以,该目标的速度、航向参数为
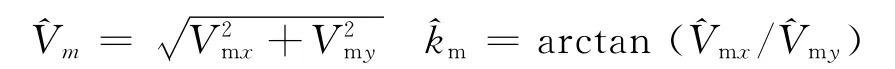
由于依赖于高度Zh,只有Zh已知,Dj才有解,所以此类方法只能针对海上目标进行定位;而对高度未知的岸上目标,该算法将无法工作.
设空中平台导航设备的高度测量误差为δZh,光电吊舱的角度测量误差为δε,对式(1)求微分,得
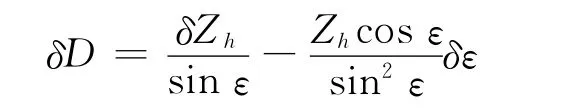
考虑到高度误差与角度误差互相独立,斜距离的定位误差均方差为
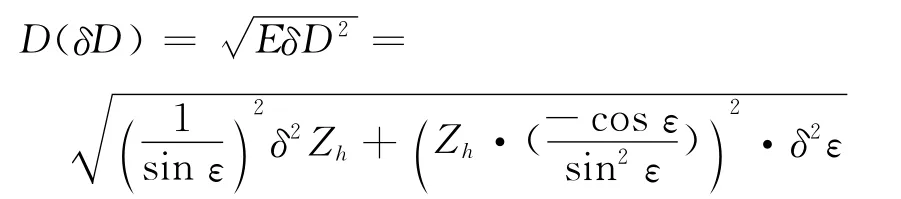
在空中平台高度一定(Zh=4 000m),导航误差、角度测量误差一定(δZh=1.5,δε=0.5)的条件下,斜距离的定位误差均方差δD随斜距离D的变化曲线见图2.

图2 目标斜距离定位误差均方差曲线
随斜距离增大,斜距离的定位误差均方差随之增大.因此,这种方法无法对观测噪声的干扰进行平滑滤波,从而也就无法达到较高的定位精度.
只有消除随机噪声对定位参数的干扰,才能提高系统定位精度,采用基于随机参数平滑的目标定位模型是最佳选择.基于此,本文提出了一种基于最小二乘的目标定位方法.
3 基于最小二乘的目标定位方法
设空中平台航向Kw、航速Vw,在初始时刻t1,目标相对空中平台的初始斜距为D1,俯仰角ε1、方位角β1;在时刻tj,目标相对空中平台的斜距离为Dj,俯仰角εj、方位角βj.设目标作匀速直航,未知航向为Km,未知航速为Vm.目标运动的几何态势见图3.
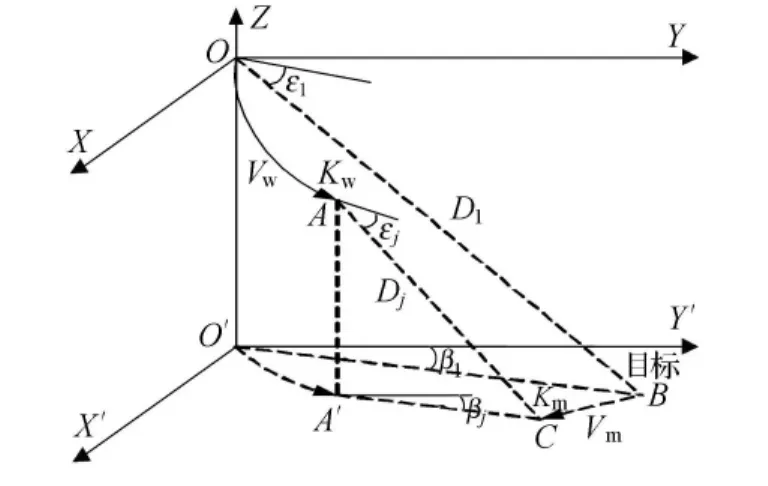
图3 目标运动几何态势图
根据相对运动的空间几何封闭性原理,由图3中4边形O′A′C′B′,得
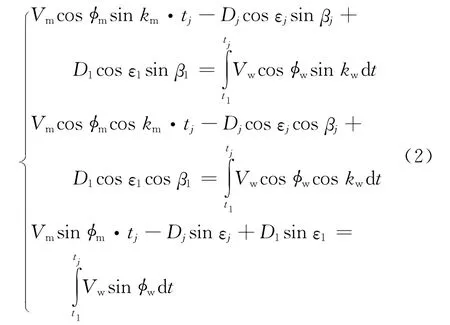
式中:φm为目标俯冲角;φw为空中平台俯冲角.
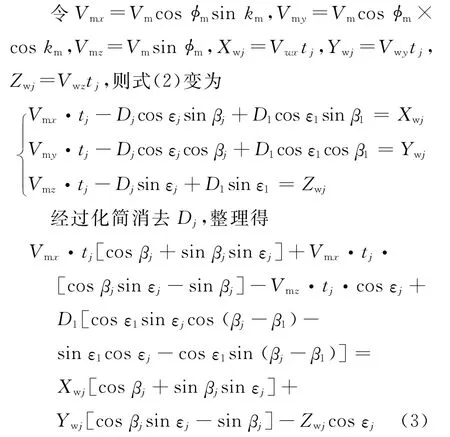
由于测量误差的存在,式(3)一般不严格满足,此时,可得
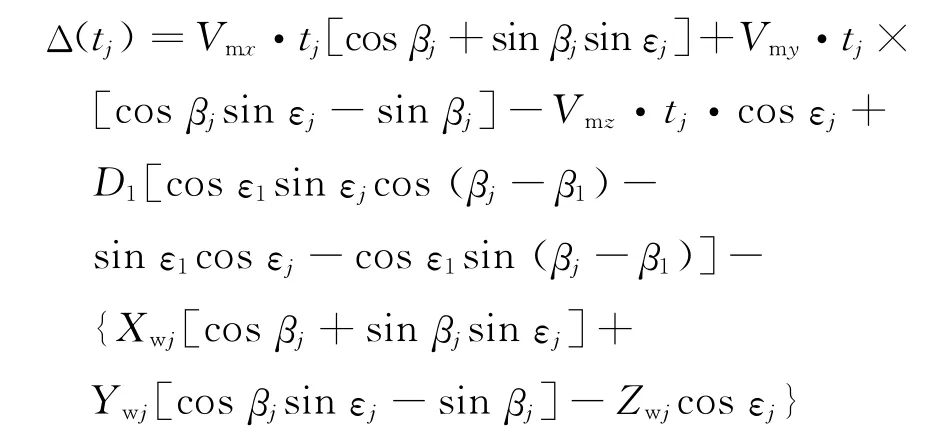
经过k次观测,基于最小二乘估计原理[10],定义如下极小化目标函数

为求得参数Vmx,Vmy,Vmz和D1,分别对其求偏导,并使∂J/∂Vmx=0,∂J/∂Vmy=0,∂J/∂Vmz=0,∂J/∂D1=0.经过整理,最终可以得到目标的运动参数

4 仿真分析及试验验证
4.1 仿真分析
以空中机动平台的初始位置为坐标系原点,空中平台以航速30m/s、航向30°机动;目标在坐标系中的初始坐标位置为(5 000,5 000,-3 500),并以航速10m/s、航向60°运动.同时,假定光电吊舱对目标的角度测量精度为0.5°,空中平台自身位置的测量精度为1.5m,以1s的时间间隔、生成300s的仿真数据.
分别利用传统的三角几何定位法和本文提出的最小二乘方法,对目标进行定位.经100次蒙特卡罗仿真后的结果,见图4~5.
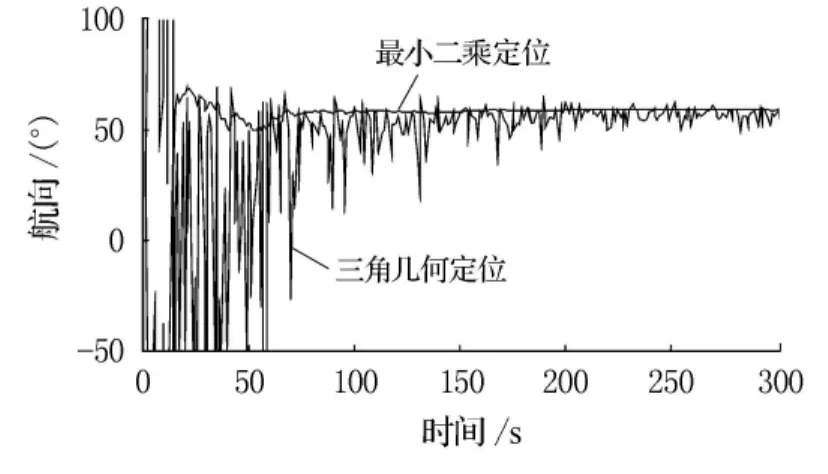
图4 目标航向收敛过程

图5 目标航速收敛过程
由图中可以看出,三角几何法定位结果虽然也能趋近于真实值,但波动大、精度不高;相比之下,本文提出的基于最小二乘的方法则收敛速度快、结果稳定、而且定位精度高.估计航速相对真实航速的相对误差小于4%,航向误差均方差为0.59°,可满足实际应用要求.
4.2 试验验证
为进一步说明算法的有效性,选用某次试验数据加以分析.当时试验情景为:以空中机动平台的地面静止控制站作为光电吊舱的跟踪目标;机动平台以变速率绕目标做圆弧机动.根据本文提出的算法,得到目标经度的收敛过程,见图6,并得到图7所示的空中平台与目标间的距离与真实距离的比较曲线.
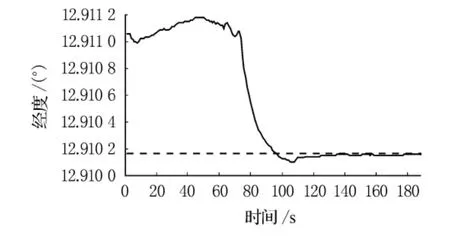
图6 目标经度
由对试验数据的分析也可看出,本文提出的算法收敛速度快,100s左右可稳定到真值附近;定位精度高,位置误差(经度、纬度)不超过0.001°,距离误差则可达到10m级,因此能够满足快速、高精度指示目标的实际需求,从而也为无源定位领域提供了一种新的可实现工程应用的方法.
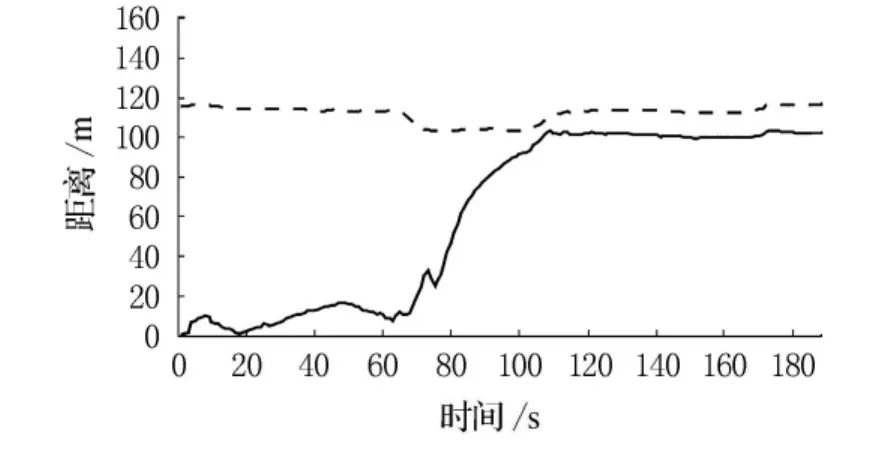
图7 空中平台与目标间的距离
5 结束语
无源定位是探测、跟踪目标的重要方式,而光电吊舱又成为无源定位的一种关键手段.利用空中机动平台搭载光电吊舱实现对目标定位已开始得到应用.结合本文所述的应用背景,在分析传统定位方法特点的基础上,本文提出了基于最小二乘的目标定位方法.仿真数据和试验数据都表明,新方法能够有效抑制测量噪声带来的累积误差,收敛速度快、定位精度高,能够满足实际工程应用需求.
[1]邹勇华,陈福胜.机载红外警戒吊舱及其研制思路[J].舰船科学技术,2001,6(1):41-44.
[2]胡来招.一种快速机载无源定位方法的分析[J].电子对抗技术,2001,16(1):1-4.
[3]何 友,修建娟.空中超视距目标三维无源定位算法研究[J].雷达科学与技术,2003,6(1):18-21.
[4]陈 玲,李少洪.无源测向测时差定位算法研究[J].电子信息学报,2003,25(6):771-776.
[5]吴世文.机载无源定位系统的定位精度[J].电子对抗技术,1995(1):27-30.
[6]JULIER S,UHLMANN J K.A new method for the nonlinear transformation of means and covariances in filters and estimators[J].IEEE Trans A C,2000,45(3):477-482.
[7]ZHANG H M,DENG Z L.A UKF based attitude determination method for gyroless satellite[J].Journal of Systems Engineering and Electronics,2004,15(2):105-109.
[8]DAN S,TIEN Lichia.Kalman filtering with state equality constraints[J].IEEE Tran.Aerospace and Electronic Systems,2002,38(2):132-135.
[9]李 硕,曾 涛.基于推广Kalman滤波的机载无源定位改进算法[J].北京理工大学学报,2002,22(4):521-524.
[10]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.

