公交发车间隔模型研究＊

李发智 肖 蕾 杨东援

（同济大学教育部道路与交通工程重点实验室1） 上海 201804） （西南交通大学交通运输与物流学院2） 成都 610031）

0 引 言

目前，国内外学者对公交调度展开了大量的研究，大多都以乘客乘车成本最小化和公交公司收益最大化为目标进行调度时刻表优化.陈芳［1］在发车间隔的研究中以乘客等待时间和公交车运行费用为目标，通过权重法结合两目标，分时段建立调度时刻优化模型，采用步长法进行仿真求解.张无非等［2］从原始数据处理到公交调度模型求解进行了研究.他们直观地从车站客流变化入手，以乘客的等待时间和公交公司的利益为目标进行优化，然后求得发车间隔.在模型建立中，对乘客等待时间量化引入罚函数机制，避免乘客等待时间过长.戴连贵等［3］分时段考虑发车间隔优化，比较详细地将乘客时间价值分成2部分：（1）乘客在车站的停留时间；（2）乘客的乘车时间.其中乘车时间又包括2站间的行驶时间、乘客下车时间、车上乘客停站等待时间.孙文霞等［4］假设公交车单位时间运营成本固定，认为乘客费用包括2部分：（1）在公车上的拥挤费用；（2）等车费用，且单位运费固定，建立公交调度模型，运用解析法求解.Andrede和Robin［5］将公交调度看成N中位问题，运用选址理论，分别考虑线性模型和环模型.朱金寿等［6］以小时为时段建立公交发车间隔模型，并设计求解算法.杨海军等提出了一种旨在快速响应乘客出行需求的“小粒度”频繁调度方法，构建了以“小粒度”时段为调度周期的多目标优化模型［7］.本文将公交线路处理成只有首末站的两点间运输，将中间站客流变化规律平移到首站，按照客流属性进行时段划分，以乘客的等车时间最小化和车辆的载客率最大化为目标，建立公交调度模型.

1 模型假设和符号系统

1.1 模型假设

1）公交线路上只有2个站，即首末站.实际中的公交线路还有一定数量的中间站，本文将中间站的客流处理到起点站，详见客流特征提取部分.

2）公交运营以乘客利益为主要目标，同时兼顾资源（在此主要指车辆）的利用率（满载率）.由于公共交通具有属准公共物品，具有很强的社会公益性，且其外部效应远远高于公交内部收益，同时，国家和地方财政给予公交一定的支持，所以，本文以乘客时间成本最小化为目标.另外，资源的合理配置利用是公交面临的又一棘手问题，所以本文以公交车辆载客率为目标.

3）车辆能承载候车的所有乘客.城市公交的发车频率大，后一辆车基本上能承载前后两辆车的时间间隙内达到的所有乘客.

1.2 符号系统

2 客流特性提取

本文考虑单条公交线路的调度问题.通过调查可获得每个站点在各个时刻的上下客人数.第i车辆到达第j个公交车站的时间是，整条公交线路有M个公交车站，在调查日的发车次数为N次.则到达站台j的公交车时刻表为…，并且有的时间间隔为，上车的人数为），乘客到达率）为

三次样条是工业生产中应用较广的插值方法，该方法可以得到平滑并且二阶可导的曲线，但由于三次样条插值要求样条曲线必须经过样本点，这使得因样本数值的变化而曲线发生剧烈变化.所以，在此用平滑样条（有理B样条）来处理乘客到达率，平滑样条得到的曲线较为平缓，并且并非必须经过样本点.根据常州市B22公交线路2010年6月11日的调查数据，拟合得到站点乘客到达率曲线，见图1.

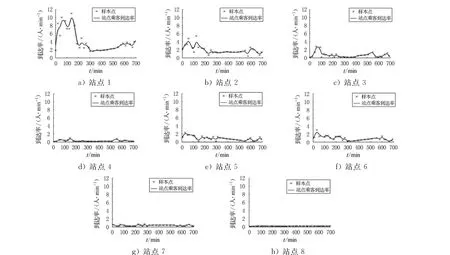
图1 各站（站1到站8）乘客到达率曲线

公交首站（第1站）到站j的运行时间为tj0，则时间t在站点j的乘客乘坐车次在首站发车时刻为t－tj0（见表1和图2）.通过平移时间tj0，将站点j的乘客到达率转换为首站乘客到达率，当把所有的中间站乘客到达率都平移到首站，则线路的乘客到达率即为首站的乘客到达率，达到率表达式为

表1 各站运行时间间隔

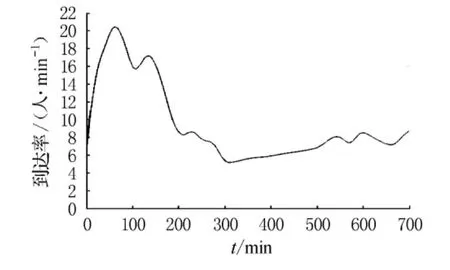
图2 公交线路乘客到达率

3 调度时段划分

以步长为Δl为时间刻度（比如10min）将一天内的发车总时长等分，则有刻度0，Δl，2Δl，…，kΔl，…，KΔl，T.其中：0为首班车发车时间，T 为末班车的发车时间，K＝［T／Δl］为下取整，聚类中不考虑首末班车，将其合并到第一个和最后时段.则有中间时刻对应的乘客到达率为

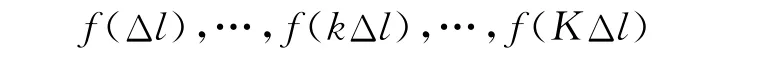
各时刻的乘客到达率组成一维有序样本.为了方便，将f（kΔl）简化为fk.按照某一划分规则，将其划分为 P（K，s）：｛fi1，fi1＋1，…，fi2－1｝，｛fi2，fi2＋1，…，fi3－1｝，…，｛fis，fis＋1，…，fK｝.其中：1＝i1＜i2＜…＜is＜K.

定义1 类｛fi，fi＋1，…，fj－1｝的相似度S（i）

定义2 相邻2类｛fi，fi＋1，…，fj－1｝，｛fj，fj＋1，…，fj－1｝的距离

由定义可见，D（i，j）越大，类之间的差异性越显著.

定义3 分类P（K，s）的误差函数

式（7）表示分类数不得少于s0，s0为常数，取2.

根据聚类优化模型，将该公交线路的客流达到曲线数据聚成5类为最优结果（见表2和图3）.

表2 聚类结果

图3 聚类结果图

4 公交调度模型

基于调度时段划分，该部分的公交调度模型，只对某一时段［Ta，Tb］进行分析即可.设定发车间隔为Δt，则发车时刻为Ta＋Δt，Ta＝2Δt，…，Ta＋NΔt，其中，Nab为该区段的发车总数，Nab＝［（Tb－Ta）／Δt］.发车间隔内到站的乘客数Fi为

式中：α为时间价值系数.时间价值系数即时间价值成本，包括隐性成本和显性成本.隐性成本是指因时间延误造成的隐性损失，如公司的迟到处罚，体现形式为罚款、奖金折扣等.显性成本指时间延误的直接损失，如不能按时到岗的生产力损失，体现形式为工资损失等.在此简化处理，隐性成本按30元／min计量，显性成本根据平均工资计算为0.28元／min（＝3 000／（22×8×60）），设定有隐性成本的乘客比例为4%，时间价值期望α为1.47元／min（＝30×4%＋0.28×96%）.

车辆的载客率定义为最大断面车内人数与最大荷载之比.当将公交线路简化成仅有首末站时，其车内人数即为最大断面载客数量，然而实际情况是在中途各站均有上下客，所以最大断面载客数小于发车间隔内的乘车人数，在此用第i辆车的折算系数λi进行处理.折算系数可以通过调查客流数据统计得到.在同一调度时段内，不同车次的折算系数变化较小，可视为常数λ.即有

式中：¯F为公交车的最大荷载量；λi，λ为折算系数.

整个调度时段的平均载客率为

其中：式（13）以乘客候车时间最小化为目标；式（14）以车辆的平均载客率最大化为目标；约束（15）为发车间隔区间约束，高峰时段为［2min，10min］，平峰时段为［5min，30min］，若既有高峰时段，又有平峰时段的区间，该约束区间为［2min，30min］.见表3.

该模型是一个多目标规划，为了便于求解，将多目标化为单目标.将目标（14）划成如下约束

式中：η0为载客率下限，平峰时段一般取60%，高峰时段取80%.

根据第三部分的聚类结果，求解区间［21，176］内的发车间隔.该区间对应的时段是［06：51，09：26］，为高峰时段，发车时刻约束［Δt′0，Δt″0］为［2min，10min］.根据实际情况，相关参数取值为：¯F，100人；α，1.47元／min；λ，0.8；η0，80%.经模型计算，最优发车时间间隔为6min.见表3、表4.

表3 计算结果

表4 发车时刻表

5 结束语

本文以常州公交线路B22跟车调查数据为支撑，建立了一套确定发车时刻表的方法.该方法分为3步骤：（1）拟合乘客到达率曲线，采用时间平移将中间站的客流特征转化到公交首站，简化了调度模型建立过程；（2）结合Fisher有序样本聚类思想，建立划分调度时段的优化模型，划分调度时段；（3）结合前2部的成果，综合考虑乘客等车时间成本和车辆的利用率，确定发车间隔.全文以实证研究为主，整套方法简洁地计算出发车时刻表，经调查数据验证了模型和方法的可行性和实用性.

［1］陈 芳.城市公交调度模型研究［J］.中南公路工程，2005，30（2）：162－164.

［2］张无非，张 驰，严奇琦.对于公交汽车调度问题的求解［J］.工程数学学报，2002，19（S1）：81－88.

［3］戴连贵，刘正东.公交调度发车间隔多目标组合优化模型［J］.交通运输系统工程与信息，2007（4）：43－46.

［4］孙文霞，宋 倜，乔国会.公交调度中发车间隔控制研究［J］.河北工业大学学报，2007，36（2）：89－93.

［5］ANDREDE P，ROBIN L.Optimal timetables for public transportation［J］.Transportation Research Part B－Methodological，2001，35（8）：789－813.

［6］朱金寿，朱 琪，杨勇刚，等.公交车调度方案的研究［J］.武汉理工大学学报：交通科学与工程版，2002，26（2）：169－171.

［7］杨海军，贺国光.基于快速需求响应的城市公交在线调度方法研究［J］.武汉理工大学学报：交通科学与工程版，2009，33（3）：430－433.