有限元方法在船用超声液位传感器瞬态特性分析中的应用＊

史日安 贺 国 王 豪1， 蔡红升

（92196部队1） 青岛 266011） （海军工程大学船舶与动力学院2） 武汉 430033）

0 引 言

某型超声液位传感器能对各舱定点液位进行实时有效的监控，其振动特性、辐射声场和输出电压等参数都是时间的函数，因此瞬态特性分析对传感器能量传输转换和信号特征研究有重要的意义.经典等效电路法和解析法在建立瞬态特性分析模型时，要进行一系列简化、假设和繁琐的解析计算，处理复杂结构问题时存在局限性.有限元方法是一种精确的数值计算方法，可以更真实的模拟工程实际，解决多物理场耦合问题，便于计算辐射声场及输出电压等诸多性能参数.ANSYS软件是目前比较流行的大型有限元软件之一，其Multiphysics功能模块提供了一个易于应用的多物理场求解分析模块［4］.利用ANSYS有限元软件，可对超声液位传感器瞬态特性进行仿真分析，求解声场分布及其输出电压等问题.

1 结构设计特点与工作方式

某型超声液位传感器主要由发射探头、接收探头组成，用于船舶的水舱、油舱、油水混合污水舱和发动机的进排气系统管道等液态介质的液位监测.传感器结构如图1所示.

图1 超声液位传感器结构图

传感器采用发射接收分离式的结构形式，既避免了发射型超声液位传感器要求安装在容器顶部带来的安装和液位监测盲区问题，同时又克服了多发多收难以消除多路之间相互耦合可靠性差等技术问题.为克服金属活化性能差、不易与压电元件粘接的缺点，压电陶瓷前端通过高温粘结剂与金属保护膜粘接，以保证高温条件下实现良好的声传递.采用空气作为背衬可以提高传感器工作频率的稳定性和灵敏度.压电元件采用后盖板、弹簧和弹簧座进行固定，弹簧座为绝缘性材料，可直接压在导电环上.通过控制弹簧的形变施加一定的预应力，增大了压电振子的阻抗，以提高所能承受的发射功率.弹簧座采用绝缘材料作为预应力弹簧承载结构.为了适用海水等腐蚀性的工作环境，传感器的壳体选用耐腐蚀性能好的不锈钢材料.

相对于水或油等液体介质，空气的阻抗非常小，发射探头发射的超声波能量会迅速衰减，接收探头收到的超声信号非常微弱.超声液位传感器就是利用该差异实现对定点液位的监测.只有当水或油充满发射和接收探头的时候，接收探头才会接收到强的超声信号，并转换成一定形式的电压信号，通过分析比较与空气中输出的电压信号特征的不同就可以实现液位定点监测报警和控制功能.

2 瞬态特性分析的有限元方法

2.1 瞬态动力学分析的有限元求解原理

瞬态动力学分析是用于确定承受任意时间变化载荷结构动力学响应的一种方法.利用瞬态动力学分析的方法，可以确定在已知瞬态载荷作用下结构体的应力、电势、位移和应变等参量随时间的变化情况.利用ANSYS软件进行瞬态特性分析，在处理结构力学线性问题所依据的有限元方程为

当然，光营造氛围还是不够的，利丰雅高同时也在用“智慧”用人留人：1.提供广阔的平台，给予员工充足的信任。相信每个人都是发自内心地努力做好自己的本职工作，放手让员工完成自己的工作，建立管理者和员工之间的双向信任；2.建立健全培训制度和培养机制。员工培训有利于激发员工积极性、提高员工满意度，增强凝聚力。外部营造氛围，内部完善体系，由内而外落到实处。

ANSYS求解器的内核是面向诸多广义生成数学模型的普适求解器，若将各参数矩阵、位移向量和载荷向量都考虑成广义涵义，则所有物理场的线性问题都可等效为式（1）的形式，用统一的求解器进行求解.

2.2 超声液位传感器瞬态特性分析的有限元方程

压电材料的压电特性涉及到电学量和力学量之间互相耦合作用，基于压电材料电场必须和弹性位移场相互平衡的条件，压电耦合作用可描述为

式中：T为应力；D为电位移；S为应变；E为电场强度；cE为弹性常数矩阵；e为压电常数矩阵；εS为介电常数矩阵.

流体中声压p的波动方程［5］

式中：cf为流体中的声速.

有限元分析所依据的能量变分原理［6］的数学表达式为

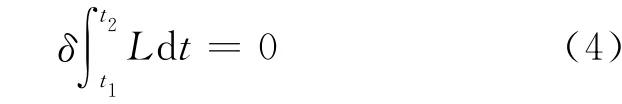
式中：拉格郎日函数L可用式（5）表示：

式中：TD为系统的动能；UM为弹性应变能；WM为外界机械力所做的功；UE为电场中的电能；WE为外界电场所作的功.令ρ为结构密度；u为位移；ρV为体力密度；ρS为面力密度；φ 为电位；q为自由体电荷密度；σ为自由面电荷密度，则拉格郎日函数表达式中诸分量由式（6）确定.

将式（2）～（6）联立，经过剖分插值，利用变分等于零的条件，作一系列推导即可得到压电－结构－流体耦合的控制方程［7－9］

式中：Muu为压电体质量矩阵；Cup为流体－结构耦合矩阵，CuP＝CTPu；P为机电耦合向量；Kuu为压电体刚度矩阵；KuV为机电耦合矩阵，KuV＝KTVu；V为电极面上的电势；F1（t）为载荷向量；KVV为介电刚度矩阵；Q为电极面上自由电荷电量；MPP为流体质量矩阵，KPP为流体刚度矩阵.将式（7）扩充为广义矩阵方程（8），压电－结构－流体耦合问题可利用瞬态动力学分析的求解器求解.

3 有限元建模与求解

3.1 有限元建模

有限元建模过程，也是实际的物理问题离散化的过程.通过几何建模、材料参数输入、单元类型选择、网格划分和载荷施加等步骤，将实际物理问题转换成待求解的有限元问题，并利用ANSYS软件的后处理器将有限元方程的解转化为具体问题的解.图2是某型超声液位传感器的有限元模型.

图2 某型超声液位传感器有限元模型

表1 某型超声液位传感器相关材料特性参数

考虑到减少计算量和方便网格划分等因素，建立某型超声液位传感器的平面几何模型.分析传感器所需要的单元类型包括：流体单元、耦合场单元、结构单元和弹簧单元等.在PLANE13单元中，选择压电选项即可实现压电陶瓷的压电耦合建模分析；有限和无限远的流体分别用FLUID29单元和FLUID129单元模拟；弹簧采用COMBIN14单元模拟；其他结构单元采用PLANE42单元模拟.

压电材料属于各向异性材料，介电常数矩阵、弹性常数矩阵和压电应力常数矩阵会随着极化方向的改变而不同，极化方向相反的压电陶瓷压电应力矩阵取反，其他参数相同.密度、声速和声吸收系数是流体介质的有效参数，其中声吸收系数MU的取值范围为0～1之间，MU＝0表示介质无吸收，MU＝1表示完全吸收状态.表1为某超声液位传感器相关材料特性数.

合理地调整有限元网格的密度，既可使求解精度满足要求，又能节约计算成本.对于某型传感器的有限元建模，单个波长范围内要划分20段以上［10］.厚度振动模式条件下，压电陶瓷的谐振频率fr和反谐振频率fa满足

式中：Kt为压电陶瓷的有效机电耦合系数，通过式（8），（9）求得fa＝0.945 58MHz，fr＝0.839 12 MHz.设声速cc为超声波在压电陶瓷内的传播速度，则网格大小ΔL可表示为

将cc和fr代入式中，得ΔL为0.262 2mm；为划分网格方便，取ΔL＝0.2mm作为单元长度.

准确的从具体问题中抽象出反映问题本质的载荷，是建立有限元模型的前提条件.载荷主要包括已知的约束条件、边界条件和激励条件等.如图2，某型超声液位传感器主要包括对称边界条件、等电势边界条件、流体结构耦合边界条件和声场无限远边界条件等载荷.

3.2 求解方法及其相关参数选取

求解瞬态特性主要有完全法、缩减法和模态叠加法.3种方法中，完全法功能最强大，允许施加各类非线性特征（塑性、大变形和大应变等）.而模态叠加法不允许施加强制位移，缩减法又不能施加单元载荷（压力，温度等），因此在计算条件允许情况下，采用完全法计算分析的效果最好.

3.2.1 积分时间步长的选取 瞬态分析求解的精度取决于积分时间步长的大小.步长越小，精度越高，但会占用大量计算机资源.选择最优时间步长可遵循如下原则：（1）求解响应频率时，时间步长必须足够小.采用Newmark时间积分方案，时间步长ITS取为1／20fr时，可求得比较精确的解；（2）求解载荷与时间关系时，时间步长应小到足以“跟随”载荷函数.响应总是滞后于所加的载荷，对于阶跃载荷尤其明显，因此在阶跃时间点附近，时间步长ITS应更小，可取为1／180fr.

3.2.2 瞬态积分参数的选取 采用Newmark时间积分方案，主要积分参数有二阶瞬态积分参数（GAMMA，ALPHA，DELTA）、一阶瞬态积分参数（THETA）、一阶扰动极限准则（OSLM）和光滑选项（AVSMOOTH）等.进行瞬态压电特性分析时，推荐取ALPHA＝0.25，DELTA＝0.5，THETA＝0.5，其他参数则可采用ANSYS软件设定的默认值.

4 仿真计算与实验验证

利用ANSYS软件建立某型超声液位传感器有限元模型，传感器激励源采用周期为2ms、占空比为25%的方波脉冲，其高电平和低电平分别为5V和0V，分析一个周期时长的传感器瞬态特性，计算该传感器周围流体的超声场分布、输出电压等.

4.1 传感器辐射声场及输出电压的仿真计算

对于单个节点声压、电压等变量的瞬态响应，通过ANSYS软件时间后处理器（post26）得到该变量在时域范围内的响应，对于流体某一时刻的声压通过通用后处理器（post1）得到.接收探头中心点声压的瞬态响应及1.75ms时刻流体声场见图3.

图3 仿真结果

从图3可见，采用空气作为背衬、不锈钢作为保护膜，超声液位传感器输出电信号出现双峰现象；压电陶瓷激励产生的超声信号在探头保护膜存在强烈的反射，多次反射使得接收探头输出电压信号存在较强的余振；超声波主要在探头之间的间隙传播，发射探头发射的超声波和接收探头发射的超声波在探头间隙流域产生干涉现象.

4.2 实测实验

实验是检验建立模型正确与否的主要方法.如图4所示，实验平台主要有ATG3021B信号发生器、水池、传感器、PCI－50614数据采集卡和计算机组成.通过图3和图4比较可以发现：有限元模拟计算结果和实验测量结果两者的波形具有较好的一致性，说明所建立的有限元模型计算仿真特性和实际传感器特性相同.因此，该模型可用于超声液位传感器的设计与研究.

5 结束语

超声液位传感器作为能量转换和传递的系统，很难用传统的解析法对其瞬态特性进行准确的求解分析.有限元方法是一种有效的声学传感器分析方法，借助有限元瞬态特性分析技术，利用ANSYS软件可以很好的解决某型超声液位传感器瞬态特性仿真分析问题.有限元方法建立的仿真模型计算结果与实验测量结果两者波形具有较好的一致性，证明了基于有限元方法的传感器瞬态特性分析方法的有效性，同时该方法也可用于超声液位传感器的设计研究.

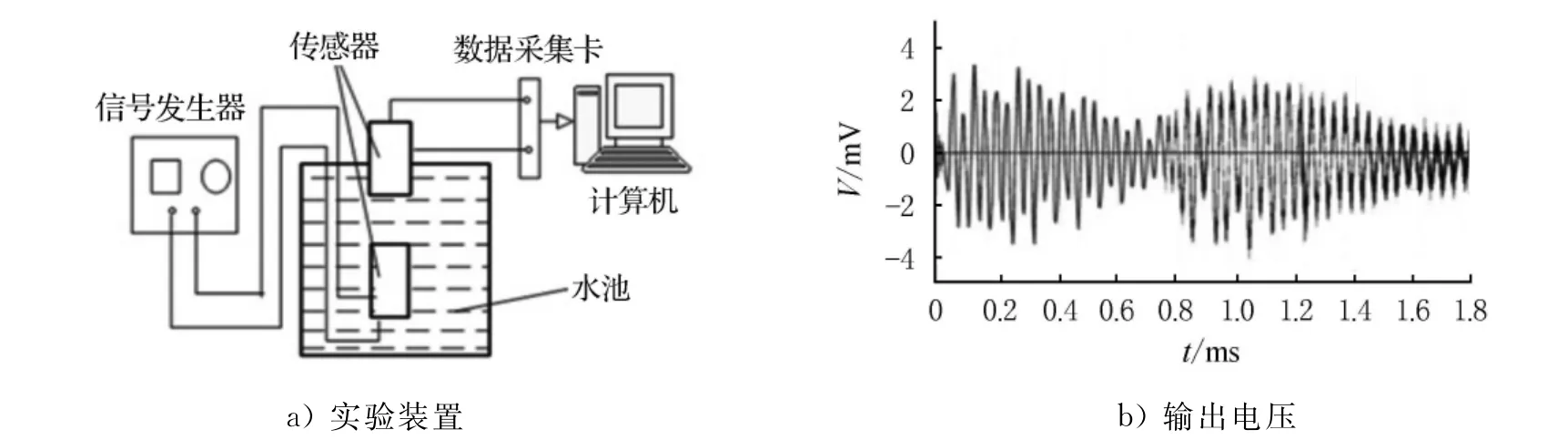
图4 传感器实验装置及实验结果

［1］温淑慧.一种高精度超声液位测量系统的研究［J］.压电与声光，2002，24（6）：494－496.

［2］WANG Hao，HE Guo，MING Tingfeng，et al.Dynamic modal of shipborne ultrasonic liquid level trasducer and its simulation［C］／／2011International Conference on Electrical and Control Engineering，2011：1531－1534.

［3］明廷锋，贺 国，王 豪.船用超声液位传感器的分析与设计［J］.应用声学，2011，30（1）：53－57.

［4］曾 攀.有限元分析及应用［M］.北京：清华大学出版社，2004.

［5］莫西平.ANSYS软件在模拟分析声学换能器中的应用［J］.声学技术，2007，26（6）：1279－1290.

［6］HILL R，FORSYTH S A.Finite element modeling of ultrasound，with reference to transducers and AE waves［J］.Ultrasonics，2004，26（42）：253－258.

［7］BATHE K J.Finite element procedures［M］.Englewood cliffs：Prentice－Hall Inc，1996.

［8］EVERSTINE G C.Finite element formulation of structural acoustics problems［J］.Computers ＆Structures，1997，65（3）：307－321.

［9］邢景堂，周 盛，崔尔杰.流固耦合力学概述［J］.力学进展，1997，27（1）：19－38.

［10］Yago Gomez－Ullate Ricon，Francisco Montero de Espinosa Freijo.Piezoelectric modeling using a time domain finite element program［J］.Journal of the European Ceramic Society，2007，27：4153－4157.