浅谈Routh-Hurwitz判据中的若干应用

俞 菲，孟 桥，樊祥宁

(东南大学 信息科学与工程学院，江苏 南京210096)

0 引言

对于线性时不变系统而言，系统稳定性的判断是“信号与系统”课程中系统分析的基本问题之一，也是稳定性授课的重点。Routh-Hurwitz 准则可以提供简便的根分布判决方法。在判别的过程中，处理Routh 数列中全零行的问题是学习的难点。

［例1］根据Routh-Hurwitz 准则判别下面特征方程根的分布。

解:列出Routh 数列

上述例题中，在排列Routh 数列的过程中出现了全零行，则构造辅助多项式，利用其导函数的系数代替全零行，并可判断得知系统不稳定。如果需要判断根的分布，则需要进一步求解辅助多项式。什么是辅助多项式呢?

由Routh 表第二行元素作系数所构造的多项式gn(s2)=s4+2s2+2 是辅助多项式吗?回答为是的。由Routh 表第四行元素作系数所构造的多项式gn(s2)=s2+2 是辅助多项式吗?回答为不是，它是偶次多项式。什么又是偶次多项式呢?它和辅助多项式存在怎样的联系?辅助多项式的概念只适用于出现全零行的情况吗?

这是在“信号与系统”课程中关于系统稳定性分析时让许多学生感到困惑和难以理解的一个问题。下面我们将试图利用辅助多项式与偶次多项式，使上述问题的讲解明朗化。

1 辅助多项式与偶次多项式

考虑多项式D(s)=ansn+an－1sn－1+… +a1s +a0。当a1R(i =1.2，…，n)，a1≠0 且同号时，我们可以构造出著名的Routh 数列表，如表1所示。

如果n 是偶数，我们可以得到上表中所示的以B 为标记的偶次多项式;如果n 是奇数，我们可以得到上表所示的以A 为标记的偶次多项式。这些仅包含偶次项的多项式本身与原方程的根并没有直接的关系，但是通过偶次多项式可以构造出一族辅助多项式。其中，特征多项式就是一个特殊的辅助多项式，它是由第一和第二个偶次多项式构成:

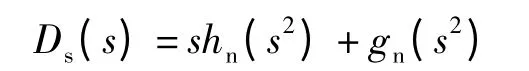
类似地，可以得到辅助多项式与偶次多项式直接的关系:

以上n 个辅助多项式的最高项系数分别对应Routh 表的第一列元素，从Dn(s)到D1(s)每计算一次，阶数降低一位，减少一个根。利用幅角原理即可证明［1］，当各辅助多项式最高项的系数始终不改变符号时，每步总是减少一个在左半平面的零点，则系统稳定。

当出现全零行时，由于出现了数值为零的偶次多项式，因此，辅助多项式恰好等于偶次多项式。由于稳定性的分析只用到了辅助多项式，所以大多数教材并没有引入偶次多项式的概念，使学生产生误解，认为偶次多项式就是辅助多项式。下面，我们针对全零行这一特殊的情况深入分析。

2 全零行的出现

在计算Routh 数列的时候，如果遇到连续两行数字相等或等比时，则下一行的元素将全部为零，此时数列无法正常计算下去。这种情况说明系统函数在虚轴或复平面的右半平面上有极点。出现全零行的原因是:所给方程至少有一对根对称地位于通过原点的直线上［2］，例如，我们有一个根σ +jω，则也有为一个根-σ－jω。我们知道在这种情况下，即使σ=0，系统也仅仅是临界稳定的。因此可以认为，只要出现了全零行，系统就不再是稳定系统。

2.1 特征根位置的判断

我们若进一步分析极点的分布，需要采用辅助多项式进行判别。由于辅助多项式是原多项式的一个因式，因此它的根也是原方程的根。此时，判定系统是否稳定除了要判别Routh 数列是否变号外，还要审查虚轴上极点的阶数。如虚轴上的极点均为单极点时，系统临界稳定;如虚轴上有重极点则系统不稳定。

［例2］根据Routh-Hurwitz 准则判别下面特征方程描述的系统是否稳定

解:全部系数都是正实数，且无缺项。排列出Routh 数列:

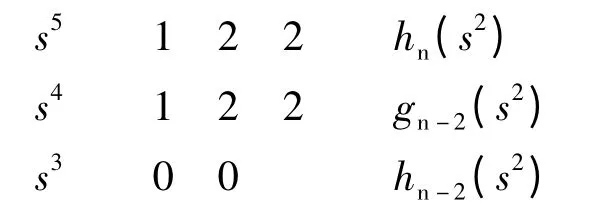
此时在Routh 数列的第三行出现全零行，数列左边所写的hn(s2)，gn－2(s2)，…一列表示用Routh表相应行元素做系数所构造的偶次多项式:

在例题中hn－2(s2)=0 时，系统的辅助多项式Dn－1(s2)=gn(s2)。所以，我们可以求解Dn－1(s2)=gn(s2)的根来判断原系统极点的分布。

令gn(s2)=s4+2s2+2 =0，可以得到四个根，分别是。这四个根成对地关于原点对称，分别有两个正实部的根和两个负实部的根，加上从D5(s)计算到D4(s)所减少的根，系统有三个负实部的根和两个正实部的根。

除上述分析方法外，另一种分析方法是利用gn(s2)=s4+2s2+2 的导函数的系数代替hn－2(s2)的系数继续判断。系统的稳定性判断不变，系统特征根可以不需要求解，而粗略判断其位置。

由于Routh 数列的首列变号两次，那么系统具有两个正实部的极点。根据全零行出现的原理:所给方程至少有一对根对称地位于通过原点的直线上，可以判断系统还有两个负实部的极点，加上从D5(s)计算到D4(s)所减少的根，我们也可以得出系统有三个负实部的根和两个正实部的根的结论。

2.2 出现多次全零行

以上我们介绍了当系统特征方程的Routh 数列出现全零行时，两种分析根分布的方法。在教学过程中，我们发现全零行有可能会多次出现，即:采用辅助多项式处理全零行继续Routh 数列的排列后，又出现了全零行。此时，可以继续采用辅助多项式来进行处理，但是有学生提出这样的疑问，如果这两个辅助多项式的根都是系统的极点，那么系统极点的个数将大于系统的阶数。

这个结论看似矛盾，但仔细分析后发现，出现多次全零行是因为系统在虚轴或复平面的右半平面上出现重极点，所以两个辅助多项式必然有相同的根。也就是说第一个全零行辅助多项式的根必然包含了第二个全零行辅助多项式的根。并且，通过观察我们发现全零行出现的次数，就等于最高次重极点的阶数。这样的系统，即使重极点出现在虚轴上，我们也可以直接认定它是不稳定的。即出现多次全零行的系统一定是不稳定系统。下面我们举例说明。

［例3］根据Routh-Hurwitz 准则判别下面特征方程描述的系统是否稳定

通过Routh-Hurwitz 准则可以判断:Routh 数列首列的系数没有变号，所以系统没有正实部的极点。但此时并不能判断系统就是稳定的，还要继续检测虚轴上极点的重数。由于系统没有正实部的极点，但Routh 数列出现了全零行，所以可以判断，在虚轴上一定成对地出现共轭虚根，分别求解两个辅助多项式的根。

令gn(s2)=s4+2s2+1 =0，可以得到s1，2= j，s3，4=-j，系统存在二重极点。再令gn－2(s2)=s2+1=0，可以得到s1=j，s2=-j。两个辅助多项式根的数值相同，阶数不同。这是因为第一次处理全零行后仅消去了一重极点，而重根的阶数仅降低了一次。

如果虚轴上存在两对共轭的虚根，但这两对根并不是重根，情况将怎样变化呢?现看这样一个特征多项式:

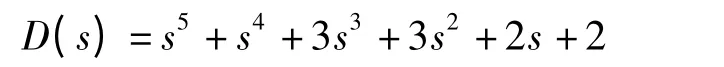
排列出其Routh 数列可以发现只出现一次全零行，且数列不变号。此时系统没有右半平面的根，求解辅助多项式可以得到系统有两对共轭的虚根，分别为

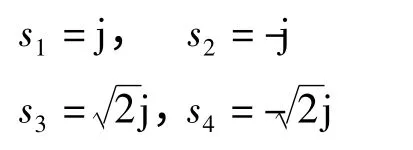
由此可以看出，全零行出现的次数仅等于系统虚轴或右半平面极点的重数，而与其个数无关。

3 结语

本文从Routh-Hurwitz 数列的原理出发，讨论了其在系统稳定性判断中的应用。我们将其作为课题讲解的难点，着重讨论了Routh 数列全零行出现的原理，及其处理的方法。

［1］ 何琴芳. 对Routh-Hurwitz 判据的进一步证明［J］. 南京:东南大学学报. 1993，23(1).

［2］ 郑钧. 线性系统分析［M］毛培法译. 北京:科学出版社.1987.