基于能量守恒定律的载流体内自感分析
朱 峰,杨晓铖
(西南交通大学 电气工程学院,四川 成都610031)
0 引言
“电磁场”是电气工程等专业的技术基础课程。从经典论著到现有的典型教科书[1~2],关于内自感和内磁链的表述,往往让人难以理解。例如取电流大小为I 的长直通载流体的一段,可以利用安培环路定理得出磁场为

式中,ρ 表示为磁场路径所包围的圆半径,I'表示磁场路径所包围的电流强度,J 表示导线中电流密度,R 为导线半径。
则整个导线的内磁通为
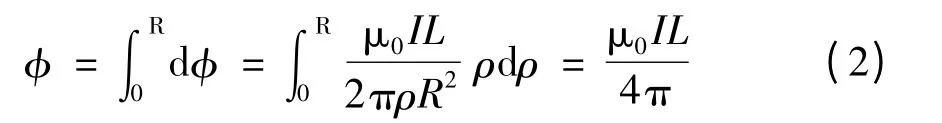
按照一般教科书的表述[2~3],可得内磁链与电流的交链微元为

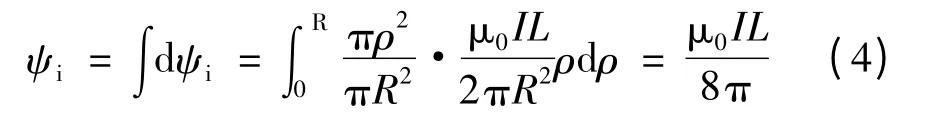
根据Li=ψi/I,可得L 长度的通电载流体的内自感系数为

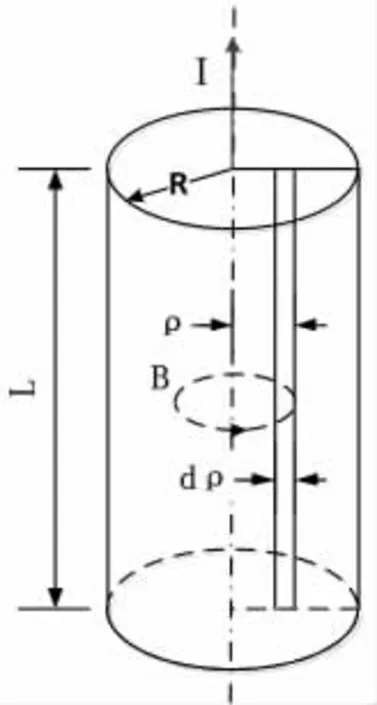
图1 内磁通、内磁链示意图
上述推算中存在一个问题,即由此得到的自感系数比直接用式(2)计算内磁通所得的内自感系数相比减小了一半。虽然文献[3]用场能的方法得出了上式的正确性,但仍然不能够物理上给出合理的解释。文献[4]谈及了此问题的复杂性,并用平均值法进行了分析,相当于加权平均,但很难理解问题的本质。笔者认为有必要从本质上理解必须经过严格的推导和论证。
按照法拉第电磁感应定律,当电流看成环“线”,即忽略电流的横截面积时,可直接利用磁通计算电感。例如,若环的外磁通为e,则外自感为

若以磁链的角度看问题,每一根磁力线由于由闭合面内传出,在外形成闭合线,完全包围了电流,故式(3)中的I'/I 一定为1,即

此时,磁链与磁通数值是相等的,这正是人们理解法拉第电磁感应定律的基础,由此而得到的自感系数一般被称为外自感Le;当载流体的横截面积不能忽略时,由式(5)结果凭空产生的1/2 因子确实无法利用法拉第电磁感应定律解释,故本文将利用能量守恒定律对式(5)进行理论分析,文献[5 -6]用过类似的方法计算自感系数。
2 横截面积不可忽略时的分析
下面对横截面积不可忽略时载流回路的交链进行分析:本文利用微元法将载流体中的电流看成由横截面无穷小的一根根“线”载流闭合回流构成,该“线”电流大小为δIi,穿过δIi构成的闭合回路磁通为i,如图2所示。如图则有
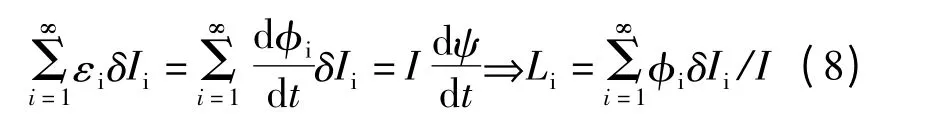
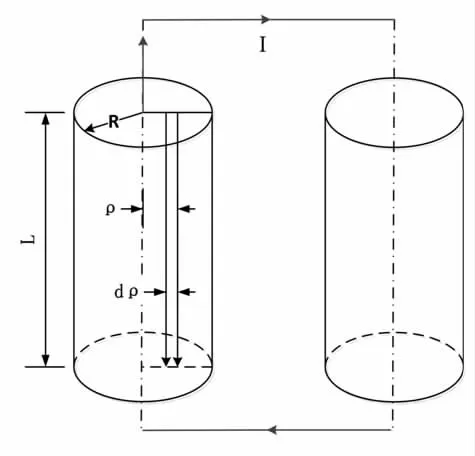
图2 无限长闭合回路之有限段
可见,对于连续载流体,电感量只是一个等效量,描述的是宏观因素将外部能量转变为磁场能量的能力,所以也称为感抗。本文研究的是载流体回路的一部分,磁通量即所对应的总磁通,包括内外磁通两个部分:①内磁通i:该电流微元构成的闭合环路所包围的磁通,即图中所示由ρ 到R;②外磁通e:电流所在导体的外边缘构成的闭合环路所包围的磁通,即外磁通。
而本文针对的是内自感,故仅考虑内磁通,如图所示电流微元所包围的内磁通的大小为

另外,以指向纸里为正参考方向时,根据
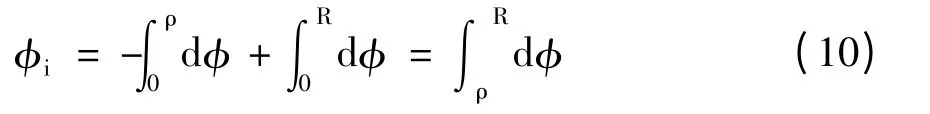
可知在导线中半径为ρ 处的任何一个电流微元所包围的内磁通均是相等的。现假设长直载流体构成的回路在无穷远处,忽略两边电流的耦合,故可对长度为L,电流大小为I 的因内自感存在而具有的场能进行如下计算。
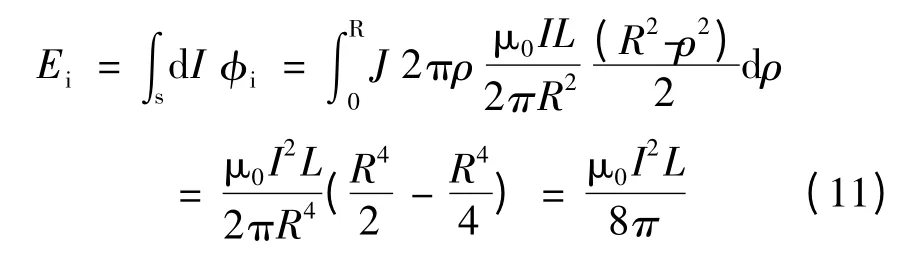
式中,J=I/πR2。可得电流与内磁通的交链ψi以及内自感Li为

由此我们得出了与式(5)相同的结论。通过以上证明可以看出,内自感不能单纯从自感本身意义去理解,而是等效概念,只能从能量角度去理解。
3 结论的一般性证明
以上证明是对长直载流体中磁回路包围电流环路与电流环路包围磁回路两种计算方法的等效,对于任意闭合线圈的证明如下。假设线圈无限长、无限宽,各处电流不存在耦合。
1)电流环路包围磁通角度
如图3所示,设环虚线Γ 处的线电流微元的大小为dI,电流的横截面大小为S',穿过虚线Γ 的磁通包括内磁通i 与外磁通e 两部分组成,对应的面积分别为S1与S2。

图3 电流环示意图
电流环路的内磁通为
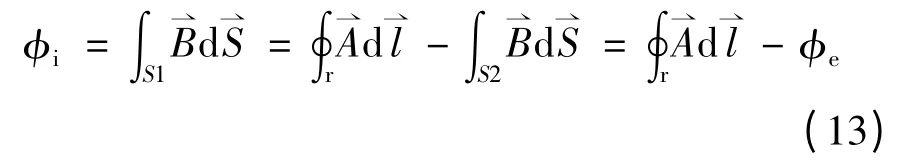
导线因电流内自感所具有的能量为

其中,dS'表示在线电流微元dI 处所取面积微元,则dI 可以表示为该处电流密度与面元的乘积。
2)磁通包围电流微元
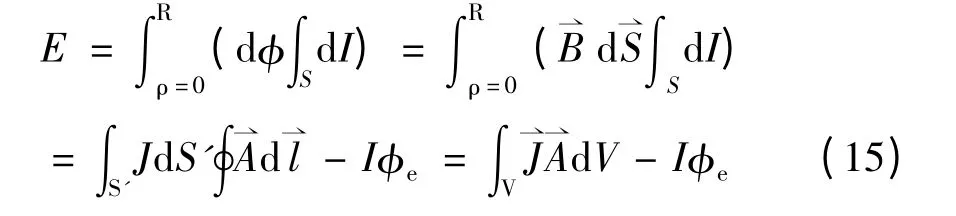
至此,我们由式(14)和式(15)完成了两种不同分析方法的等效推证。
4 结语
本文深入剖析了内自感的两种分析方法的等效性,结论表明,通过法拉第电磁感应定律和能量守恒定律才能在真正意义上理解内自感,而内自感也只是一个等效量。本研究对于理解磁场能量的物理过程以及内自感的本质是大有裨益的。
[1] J. A. Stratton. Electromagnetic Theory. [M]. McGraw-Hill BOOK COMPANY,1941. 264 ~268.
[2] Robert R. G. Yang. Electromagnetic Fields and Waves. [M].First Edition,Beijing:Higher Education Press. 2006. 185 ~189.
[3] 冯慈璋. 电磁场. (第二版).[M]. 北京:高等教育出版社.1980. 150 ~168.
[4] 张之翔.电磁学教学札记. (第一版).[M].北京:高等教育出版社. 1987. 59 ~162.
[5] 江巨浪.有横截面积的导体的自感系数[J].安庆:安庆师范学院学报(自然科学版).2000,Vol.6
[6] 闫伟,刘福平. 导体的内自感[J]. 曲阜:曲阜师范大学学报.1994,Vol.20

