带次临界指标薛定谔方程的正解
汪继秀,肖计雄
(1.湖北文理学院 数学与计算机学院,湖北 襄阳 441053;2.襄阳五中,湖北 襄阳 441021)
1 引言
本文主要研究一类拟线性薛定谔方程
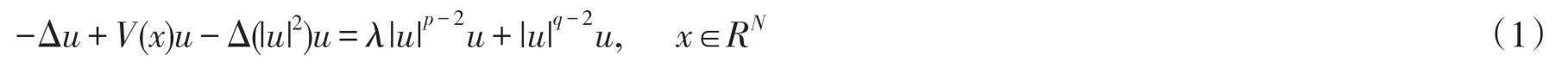
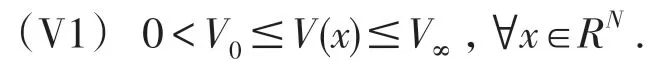
研究这类方程的动机主要源于

其中 i 是虚数单位,z:R×RN→ 复数,W:RN→R给定势能,h,l:R+→R.令z(t,x)=exp(-iEt)u(x),其中E∈R,u是一实值函数,则方程(2)转化成

若取l(s)=s,则方程(3)等价于

Poppenberg等[1]和Liu等[2]利用约束极小获得了问题(4)正的基态解.Liu等[3]利用变量替换将问题(4)转换成半线性椭圆方程,并且构建了一个Orlitz空间,利用山路引理得到问题(4)存在正解.对于这种变量替换的方法在文献[4-5]等也应用过.
本文受这些文献启发,主要考虑在方程(4)中取

即方程(1)的解.
2 主要结果
问题(1)对应的泛函

不能定义在H1(RN)上,为克服这个困难,受Liu[3]中的变量替换法的启发,令v=f-1(u),且

则有

容易验证J(v)可以定义在H1(RN)且J(v)∈C1.而且J(v)的非平凡临界点是关于

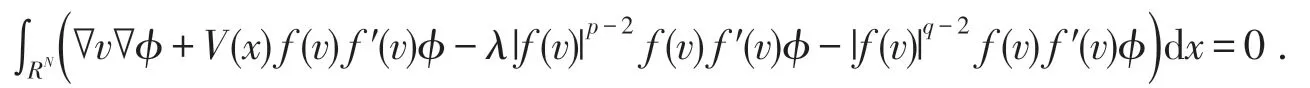
为了证明的方便,本文将问题(5)改写成

则泛函J(v)可以改写成

其中:g(x,v)=f′(v)[λ|f(v)|p-2f(v)+|f(v)|q-2f(v)-V(x)f(v)]+V(x)v,

由此我们能够证明
定理1假设V(x)是连续的径向函数且满足条件(V1),λ>0,N≥3,2<p<4,4<q<22*,那么(5)(6)(即(1))有一个正解.
证明中为了方便,记C,C1,C2…为一个正(可能不同)的常数;Lq(RN)的范数为,它也等价于H1(RN)的标准范数.
3 引理及结果证明
为了得到我们的结论,先给出几个引理.类似文献[6]关于引理2.1的证明,我们能够得到
引理1函数f(t)满足以下性质
(1)f(t)是唯一定义在C∞上函数并且可逆;
(2)∀t∈R,|f′(t)|≤1;
(3)∀t∈R,|f(t)|≤ |t|;
(4)当t→ 0 时,
(6)当t→+∞时,
(7)∃ 正数C>0 使得
并且由定理1中的条件以及引理1中的(4)和(6),则容易验证
引理2g(x,v),G(x,v)满足

引理3泛函J满足
(i)存在δ,ρ≥0,使得当‖v‖ =ρ,J(v)≥δ;
(ii)存在v∈H1(RN),使得当‖v‖ >ρ,J(v)<0.
证明由引理2我们直接有,当ε>0 充分小,则存在Cε>0 使得,

则有

这也就得到了(i).

由 4<q<22*,则当t→+∞ 时,J(v)→-∞ .因而得到(ii).
利用引理3和山路引理,令

其中Γ={γ∈C([0,1],H1(RN)),γ(0)=0,γ(1)≠0,J(γ(1))<0},则H1(RN)中存在一个关于水平集c的(PS)序列,即

引理4在定理1的条件下,J关于水平集c满足(PS)条件.
证明首先,设是(PS)序列,则有


则由q> 4 推得

另外,当|vn(x)|≤1时,由引理1(7),

当|vn(x)|>1时,由引理1(7)和(8)知

在(10)中令w=vn,结合(14)和引理1(8)则有

由(12),(13),(15)有

由2<p<4,则,使得对某一有

接下来想证

由(7)和(18),则得

因为 (J(vn))′→ 0,则由(16),(17)-(20)可得


令vn=v+vn,由f∈C1,以及(9)和Brezis-Lieb引理可知

综合(19)-(23)得
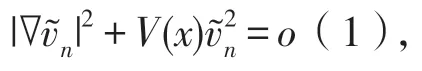
利用引理3,引理4和极值原理直接可以得到定理1.
[1]POPPENBERG M,SCHMITT K,WANG Zhiqiang.On the existence of soliton solutions to quasilinear Schrödinger equations[J].Calc Var Partial Differential Equations,2002,14(3):329-344.
[2]LIU Jiaquan,WANG Zhiqiang.Soliton solutions for quasilinear Schrödinger equations I[J].Proc Amer Math Soc,2002,131(2):441-448.
[3]LIU Jiaquan,WANG Yaqi,WANG Zhiqiang.Soliton solutions for quasilinear Schrödinger equations II[J].J Differential Equations,2003,187(2):473-493.
[4]COLIN M,JEANJEAN L.Solutions for a quasilinear Schrödinger equations:a dual approach[J].Nonlinear Anal TMA,2004,56:213-226.
[5]DO Ó J M B,MIYAGAKI O H.Soliton solutions for quasilinear Schrödinger equations with critical growth[J].J Differen⁃tial Equations,2010,248(4):722-744.
[6]SEVERO U.Existence of weak solutions for quasilinear elliptic equations involving the p-laplacian[J].Electronic Journal of Differential Equations,2008,56:1-16.

