C3×Cn的最优pebbling数
高 洁,叶永升,程 芳,史彩霞
(淮北师范大学 数学科学学院,安徽 淮北 235000)
1 引言
Chung[1]定义图G上的一个pebbling移动是从一个顶点移走两个pebble,把其中的一个pebble移到与其相邻的一个顶点上.而图G的最优pebbling数,记为fopt(G),是最小的正整数,使得把n个pebble恰当地放置在G的顶点上,总可以通过一系列的pebbling移动把一个pebble移到任何一个指定的顶点上.
将p个pebble放置在图G的某些顶点上,则称这是图G上一个类型为p的分布,记为D,|D|=p.分布到点v上的 pebble 数记为D(v),其中D(v)>0 时称点v被占领.在分布D下,D([v1,v2,v3,…,vn])=[p1,p2,p3,…,pn]表示顶点vi上分布pi个pebble,若通过一系列的pebbling 移动可以把一个pebble移到任何一个指定的顶点上,则称D是可解的.
定义1设G和H为两个图,G和H的(Descartes)积G×H是一个图,其顶点集为V(G×H)=V(G)×V(H)={(x,y)|x∈V(G),y∈V(H)},且两个顶点(x,y)与(x′,y′)相邻当且仅当x=x′,且y,y′∈E(H),或者x,x′∈E(G)且y=y′.
由此定义可将G×H视为G的每一个顶点处画出一个H的图形,并且把任意H中的每一顶点和与此H相邻的H中的对应顶点连接起来.
最优pebbling数是由Pachter 等[2]提出并研究的,关于图G的最优pebbling数,目前已有如下结论:Pn和Cn[3],超立方体[4],K2×Pn和K2×Cn[5].本文借鉴Cn的最优pebbling数的研究方法,给出C3×Cn的最优 peb⁃bling数的结论并给出证明.
为了下面证明叙述方便,我们将C3×Cn上的所有顶点进行标记.记Cn=[x1,x2,…,xn],C3×Cn=[R1,R2,…,Rn],称Ri为C3×Cn上的母线且Ri=[x1,i,x2,i,x3,i].
2 C3×Cn的最优pebbling数
我们先给出C3×Cn分别在n=3,4,5时的最优pebbling 数以及两个引理,然后推出n≥6时的最优peb⁃bling数.
定理2fopt(C3×C3)=4.
证明可找到一个可解的分布D且|D|=4,D(x1,1)=2,D(x1,2)=D(x1,3)=1.故fop(tC3×C3)≤4.下证fop(tC3×C3)≥4,即证任意类型为3的分布D均不可解.下面分3 种情况讨论:
1)当D(R1)=3 时,R2上至少有一个顶点得不到pebble.
2)当D(R1)=2,D(R2)=1 时,R3上至少有一个顶点得不到pebble.
3)当D(R1)=D(R2)=D(R3)=1 时,其余的6个顶点都得不到pebble.所以任意类型为3 的分布D均不可解,得fop(tC3×C3)≥4.
定理3fop(tC3×C4)=4.
可找到一个可解的分布D,|D|=4,D(x1,1)=D(x1,3)=2.故fop(tC3×C4)≤4.又fop(tC3×C4)≥fop(tC3×C3),由定理2 知fop(tC3×C4)≥4.即fop(tC3×C4)=4.
定理4fop(tC3×C5)=5.
证明可找到一个可解的分布D且|D|=5,D(x1,1)=D(x1,3)=2,D(x1,4)=1.故fop(tC3×C5)≤5.下证fop(tC3×C5)≥5,即证任意类型为4 的分布D均不可解.不妨设D(R1)=maix{D(R)i},下面分4种情况讨论:
1)当D(R1)=4 时,R3上至少有一个顶点得不到pebble;
2)当D(R1)=3,D(Ri)=1(2≤i≤5)时,R3上至少有一个顶点得不到pebble;
3)当D(R1)=2 时,若D(R2)=2或者D(R5)=2,则R3上至少有一个顶点得不到pebble,若D(R3)=2,则R4上至少有一个顶点得不到pebble,若D(R4)=2,则R3上至少有一个顶点得不到pebble,若D(Ri)=D(Rj)=1,(2≤i<j≤5),则剩下的两个未被占领的母线上至少有一个顶点得不到pebble;
4)当D(R1)=D(R2)=D(R3)=D(R4)=1 时,其余的11个顶点都得不到pebble.所以任意类型为4的分布D均不可解,得fopt(C3×C5)≥5.
引理5设D是C3×Cn的可解分布.如果C3×Cn中存在一条母线Ri(1<i<n)使得D(Ri)=p(1≤p≤3)且D(xj,i)≤1(1≤j≤3).那么可由D构造出一个D*且|D*|=|D|-1,使得D*是C3×Cn-1上的一个可解分布.
证明删除Ri及上的1 个pebble,将其他p-1 个pebble 恰当地放到Ri-1上,得到C3×Cn-1上的一个分布D*且|D*|=|D|-1.对于D,Ri-1可移动到xj,i上pj个 pebble,xj,i可移动到xj,i+1上至多个pebble.对于D*,Ri-1至少可移动到xj,i+1上pj个 pebble.因为,所以D*可解.
引理6设D是C3×Cn的可解分布.若D[Ri,Ri+1,Ri+2]=[2,2,0],则可以由D构造出一个D*且|D*|=|D|-1,使得D*是C3×Cn-1上的一个可解分布.
证明若Ri+1上的2个pebble分布在两个顶点上,则由引理5得证,若Ri+1上的2个pebble分布在一个顶点上,不妨设D(x1,i+1)=2.当D(x2,i)=D(x3,i)=1时,由引理5得证.否则,删除Ri+1及上的1个pebble,把另一个pebble放到x1,i上.得到C3×Cn-1上的一个分布D*且|D*|=|D|-1.对于D,设Ri可移动到x1,i+1上a个pebble,则x1,i+1可移动到x1,i+2上至多个pebble;设Ri可移动到x2,i+1上b个pebble,则x2,i+1可移动到x2,i+2上至多个pebble;设Ri可移动到x3,i+1上c个pebble,则x3,i+1可移动到x3,i+2上至多个pebble;对于D*,Ri至少可移动到x1,i+2上a个pebble,x2,i+2上b个pebble,x3,i+2上c个pebble.因为(a≥1,b,c≥0).又当a=0时,对于D,x1,i+2上至多可得1个pebble,对于D*,x1,i原来经pebbling移动至少可得1个pebble,又直接加到x1,i上1 个pebble,这2个pebble必然可以移动1个pebble到x1,i+2上.所以D*可解.
定理7fopt(C3×Cn)=n(n≥6).
证明令n=3t+r,可找到一个可解的分布D且|D|=n,D(x1,i)=2,D(x1,i+1)=1,D(x1,i-1)=0,其中1≤i≤n,且i=2(mod 3).当r=1时,令D(x1,3t+1)=1;当r=2时,令D(x1,3t+1)=D(x1,3t+2)=1.即证fopt(C3×Cn)≤n.下证fopt(C3×Cn)≥n.假设n是最小的正整数,使得fopt(C3×Cn)<n,又n-1=fopt(C3×Cn-1)≤fopt(C3×Cn),可以在C3×Cn上构造出一个最优可解分布D且|D|=n-1,由D构造出D*,使得D*是C3×Cm(m<n)上的一个可解分布,但|D*|<m,这与fopt(C3×Cm)=m矛盾,即证定理成立.
情形1C3×Cn中存在一条母线Ri,D(Ri)=1(1<i<n)(否则重新标记).
由引理 5,我们可以由D构造出一个D*且|D*|=n-2,D*是C3×Cn-1上的一个可解分布.这与fopt(C3×Cn-1)=n-1矛盾.
情形2C3×Cn中的母线只要被占领,其上的pebble数都为2.因此|D|=n-1 是偶数,从而n是奇数.在C3×Cn中一定存在连续的三个母线Ri,Ri+1,Ri+2,使D[Ri,Ri+1,Ri+2]=[2,2,0]或者[2,0,2].否则必定能找到2个相邻的母线Rj,Rj+1上所放的pebble数均为0,经pebbling移动后Rj上至少有一点得不到pebble.
(1)D[Ri,Ri+1,Ri+2]=[2,2,0].由引理 6,我们可以由D构造出一个D*且|D*|=n-2,使得D*是C3×Cn-1上的一个可解分布.这与fopt(C3×Cn-1)=n-1矛盾.
(2)D[Ri,Ri+1,Ri+2]=[2,0,2].此时D[Ri+3,Ri+4]=[2,0],[2,2]或[0,2].D[Ri+3,Ri+4]=[2,0]或[2,2]时归为(1).D[Ri+3,Ri+4]=[0,2]时,假设不出现(1),则两个相邻的母线上的pebble数必为0和2交替出现,故n为偶数,矛盾.
情形3C3×Cn中放有pebble数最多的母线为Ri(2<i<n)且D(Ri)≥3.显然,D(Rk)≠1(1≤k≤n),否则归为情形1.
(1)D(Ri)=3 时,其余被占领的母线上的pebble数为2或3.
(1.1)D(Ri-1)=D(Ri+1)=0.删除Ri-1,Ri,Ri+1及Ri上的3 个pebble.得到C3×Cn-3上的一个分布D*且|D*|=n-4.对于D,设Ri-2可移动到xj,i-1上aj个 pebble,则xj,i-1可移动到xj,i上至多个 pebble,xj,i可移动到xj,i+1上至多个 pebble,xj,i+1可移动到xj,i+2上至多个 pebble.对于D*,Ri-2可移动到xj,i+2上aj个 pebble.因为所以D*可解.这与fopt(C3×Cn-3)=n-3 矛盾.
(1.2)D(Ri-1)和D(Ri+1)至少有一个不为0,不妨设D(Ri+1)≠0.
当D(Ri+1)=2 时,与引理6证明类似,我们可以构造出一个D*且|D*|=n-2,使得D*是C3×Cn-1上的一个可解分布.这与fopt(C3×Cn-1)=n-1 矛盾.
当D(Ri+1)=3 时,若Ri+1上的3 个pebble 放在一个顶点上,不妨设D(x1,i+1)=3,或Ri+1上的3个pebble放在两个顶点上时,不妨设D(x1,i+1)=2,D(x2,i+1)=1,则删除Ri+1及上的1个pebble,将另外2个pebble添加到x1,i上,得到C3×Cn-1上的一个分布D*且|D*|=n-2.对于D,设Ri可移动到x1,i+1上a个pebble,则x1,i+1可移动到x1,i+2上至多个 pebble;设Ri可移动到x2,i+1上b个 pebble,则x2,i+1可移动到x2,i+2上至多个peb⁃ble;设Ri可移动到x3,i+1上c个 pebble,则x3,i+1可移动到x3,i+2上至多个pebble.对于D*,Ri至少可移动到x1,i+2上a+1个pebble;x2,i+2上b个pebble;x3,i+2上c个pebble.因为a,c≥0).b=0时,对于D,x2,i+2上至多得到1个pebble,对于D*,Ri上的5个pebble无论怎么分布至少可以移动1个pebble到x2,i+2.所以D*可解.这与fopt(C3×Cn-1)=n-1矛盾.若Ri+1上的3个pebble放在三个顶点上,则由引理5,我们能得到一个矛盾的结果.
(2)D(Ri)≥4 时,设D(Ri)=q,D(x1,i)=q1,D(x2,i)=q2,D(x3,i)=q3.q≥4,所以Ri上的三个顶点中至少有一个顶点上的pebble数大于或等于2,不妨令q1≥2.
(2.1)D(Ri-1)=D(Ri+1)=0.
当q=4 时,删除Ri-1,Ri+1及Ri上的2 个pebble,将Ri上的另外2个pebble放在x1,i上.得到C3×Cn-2上的一个分布D*且|D*|=n-3.对于D,设Ri-2可移动到x1,i-1上a个 pebble,则x1,i-1可移动到x1,i上至多个peb⁃ble,x1,i可移动到x1,i+1上至多个 pebble,x1,i+1可移动到x1,i+2上至多个pebble,设Ri-2可移动到x2,i-1上b个 pebble,则x2,i-1可移动到x2,i上至多个 pebble,x2,i可移动到x2,i+1上至多个 pebble,x2,i+1可移动到x2,i+2上至多个 pebble,设Ri-2可移动到x3,i-1上c个peb⁃ble,同理x3,i+1可移动到x3,i+2上至多个pebble.对于D*.Ri-2可移动到x1,i上a个pebble,x1,i可移动到x1,i+2上个 pebble,Ri-2可移动到x2,i上b个 pebble,x2,i可移动到x2,i+2上个pebble,Ri-2可移动到x3,i上c个 pebble,x3,i可移动到x3,i+2上个pebble,因为且D*时x1,i上的2 个pebble,经peb⁃bling移动后Ri上的所有顶点都有pebble到达.所以D*可解.但fopt(C3×Cn-2)<n-2.
当q≥5时,删除Ri-1,Ri+1和x1,i上的2个pebble.得到C3×Cn-2上的一个分布D*且|D*|=n-3.对于D,设Ri-2可移动到x1,i-1上a个pebble,则x1,i-1可移动到x1,i上至多个pebble,x1,i可移动到x1,i+1上至多个pebble,x1,i+1可移动到x1,i+2上至多个pebble,设Ri-2可移动到x2,i-1上b个pebble,则x2,i-1可移动到x2,i上至多个pebble,x2,i可移动到x2,i+1上至多个pebble,x2,i+1可移动到x2,i+2上至多个pebble,设Ri-2可移动到x3,i-1上c个pebble,则x3,i-1可移动到x3,i上至多个pebble,x3,i可移动到x3,i+1上至多个pebble,x3,i+1可移动到x3,i+2上至多个pebble,对于D*,Ri-2可移动到x1,i上a个pebble,x1,i可移动到x1,i+2上个pebble,Ri-2可移动到x2,i上b个pebble,x2,i可移动到x2,i+2上个pebble,Ri-2可移动到x3,i上c个pebble,x3,i可移动到x3,i+2上个pebble.因为

(a,b,c≥0).且D*时Ri上至少还有3个pebble,经pebbling移动后Ri上的所有顶点都有pebble到达.所以D*可解.这与fopt(C3×Cn-2)=n-2矛盾.
(2.2)D(Ri-1)和D(Ri+1)至少有一个不为0,不妨令D(Ri+1)=m,且D(x1,i+1)=m1,D(x2,i+1)=m2,D(x3,i+1)=m3(0≤m3≤m2≤m1).删除Ri+1及x1,i+1上的1个pebble,将其余的pebble添加到Ri对应的邻接顶点上.得到C3×Cn-1上的一个分布D*且|D*|=n-2.对于D,设Ri可移动到x1,i+1上a个pebble,则x1,i+1可移动到x1,i+2上至多个pebble,设Ri可移动到x2,i+1上b个pebble,则x2,i+1可移动到x2,i+2上至多个pebble,设Ri可移动到x3,i+1上c个pebble,则x3,i+1可移动到x3,i+2上至多个pebble.对于D*,Ri可移动到x1,i+2上个pebble,x2,i+2上个pebble,x3,i+2上个pebble.因为
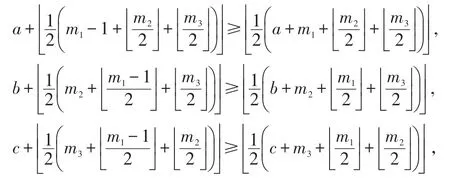
(a,b,c≥1).所以D*可解.这与fopt(C3×Cn-1)=n-1矛盾.
[1]CHUNG F.Pebbling in hypercubes[J].SIAM J Discrete Math,1989,2(4):461-472.
[2]PACHTER L,SNEVILY H,VOXMAN B.On pebbling graphs[J].Proceedings of the Twenty sixth Southeastern Internation⁃al Conference on Combinatorics,Graph Theory and Computing,Congeessus Numerantium,1995,107(3):65 -80.
[3]FRIEDMAN T,WYELS C.Optimal pebbling of paths and cycles[J].Discrete Mathematics,Submitted(Mathematics ArXiv Article Math CO /0506076).
[4]BUNDE D P,CHAMBERS E W,CRANSTON D,et al.Pebbling and optimal pebbling in graphs[J].J Graph Theory,2008,47:215-238.
[5]XAVIER C,LOURDUSAMY A.Pebbling numbers in graphs[J].Pure Appl Math Sci,1996,43:73-79.

