开关电源的系统辨识及控制算法的设计

王俊傢，张胡俊

(铜陵学院 电气工程学院，安徽 铜陵 244000)

0 引言

随着电力电子技术的发展和创新，随着各个领域对开关电源高频、高可靠、低耗、低噪声、抗干扰和模块化等方面的要求越来越高，使得开关电源［1］设计者必须从电路的设计、元器件的选取制作、电源的结构设计等方面加以更多更全面的考虑.对于开关电源来说，控制系统的设计将决定电源的主要性能优劣，故该环节是设计高精度开关电源的重要部分.

本文是在建立开关电源数学模型的基础上，针对电源精度及系统响应实时性的要求，来确定反馈控制方案.

1 开关电源系统组成

对于电源系统，为了设计其调节器，首先必须确定控制的对象，选取合适的控制变量，一般为电压或者电流，在确定了输入和输出变量的基础上建立其数学模型.采用经典控制理论设计开关电源的控制系统.

设计电源结构采用AC－DC－DC－AC－DC的方案，第一级AC－DC 采用常规380 V 经三相不控整流桥带电容滤波，输出500 V 直流;第二级DC－DC 采用高频15 kHz Buck 降压电路，输出电压的调节通过对Buck 电路的占空比调节进行;第三级至最后采用单相10 kHz 高频逆变、整流和高频电感电容滤波，用10 kHz 高频变压器进行80 k VDC 高压隔离.本文主要针对设计所述电源结构方案，利用状态空间平均法所得出的DC/DC 变换器的小信号模型，并在此基础设计相应校正方法改善电源系统性能，得出开关电源系统设计相关的结论［1］.

2 开关电源数学模型的建立

2.1 开关电源的动态小信号模型

由连续导电模式时的状态空间平均法经过平均，扰动，线性化等步骤得出输出对控制的小信号传递函数为［2］:

针对各个环节，针对开关电源各项性能指标，分别建立其传递函数，得出主回路的开环传递函数.

2.2 BUCK 电路传递函数分析

Buck 变换器一般前级整流电路会采用三相不控整流桥带大电容滤波输出直流.由于拓扑结构的限制，Buck 变换器不能隔离输出，而且输出直流电源与网测整流电压不能相差太多［3］.一般Buck 变换器的占空比设计工作在0.6 左右.输出电压与斩波电路占空比之间的传递函数.

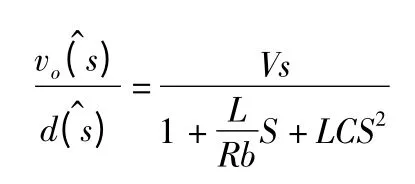
这里的L 和C 是斩波电路的参数120 uH/200 uF，而Rb 为BUCK 电路后接的等效阻抗.

在负载一定情况下，PWM 调节输出占空比是一个常量.根据计算考虑漏感损失得出比例系数为0.75，可得

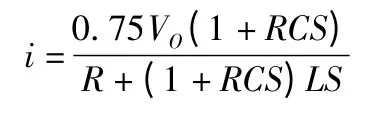
代入R=1 Ω，C=400 μF，L=780 μH 得出

得BUCK 传递函数为

2.3 逆变整流电路传递函数分析

在主回路电路中高频PWM 整流器用全控型功率开关取代了半控型功率开关或二极管，以PWM 斩控整流取代了相控整流或不控整流［1］.

电源负载电阻1 Ω，匝比k=1，逆变频率10 kHz;输出占空比大于75%;电源高频变压器的漏感必须限制在8.3 uH 以内.

所以在计算该环节传递函数的时候，在负载一定情况下，PWM 调节输出占空比是一个常量.根据计算考虑漏感损失得出比例系数为Gn(s)=0.75.

2.4 输出电路的传递函数

由R=1 Ω，C=400 μF，L=780 μH 得出此级电压传递函数为:

3 PID 控制系统方案设计

3.1 控制系统传递函数分析

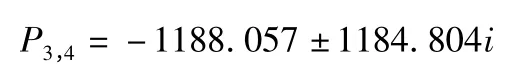
受控对象可降阶处理，近似为二阶系统，此时可以得到

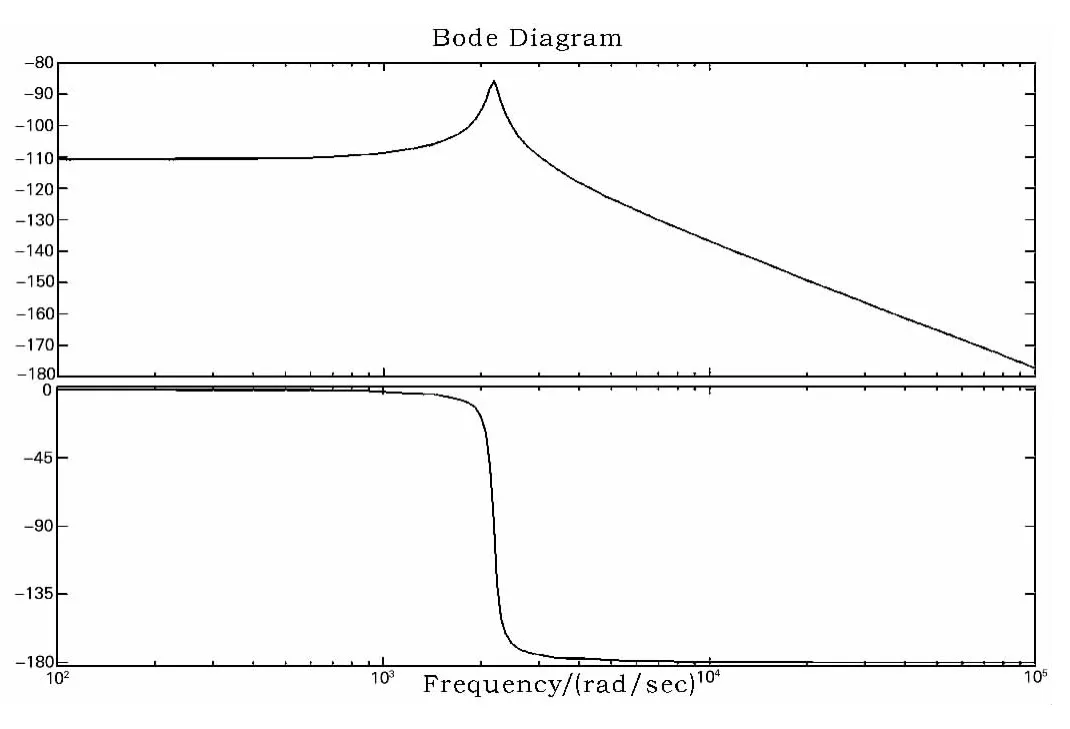
图1 未补偿前系统开环波特图fig.1 the bold plot of uncompensated open loop system

3.2 电源系统的分析与设计

对于一般的控制系统，设计者总是把它校正成Ⅰ型或者Ⅱ型系统，使得系统的稳定性容易满足要求，也能简化校正装置.而对于本设计中的电源系统，系统的输入为阶跃信号，系统的开环传递函数为二阶振荡环节，为了消除静态误差，应当加入积分环节，但是仅仅加入积分环节更加会降低截止频率，从而降低系统的响应速度［4］，牺牲了它的动态性能，而且单一的积分环节会使信号产生90°的相角滞后，对系统的稳定性不利，因此必须要加入比例环节，提高系统的截止频率.

对于本电源系统，其输入可视为阶跃信号，若将系统校正成为Ⅰ型系统，它的稳态误差为零，能够实时跟踪输入，满足设计要求［5］.

综合上述，本文设定调节器为比例积分补偿网络环节，下面来分析该调节器可行性.

加入了调节器后，其中令反馈取样系数为β=1/30，由前面的推导可知PWM 调制近似看作一个比例环节，而令补偿网络PID 传递函数记为GC(s).

比例积分(PI)调节的优点是系统稳定性好，抗高频干扰能力强，因此是PWM 控制器的常用补偿方法［6］.比例积分传递函数为

可知校正后的传递函数为

3.3 设计性能指标

3.3.1 电压精度

电源稳态精度要求为3%，则该电源允许的电压误差为ess=9 V.弧电源输入激励为阶跃信号，由上式可知，校正后系统，稳态误差为零，满足电压精度的要求，故只要考虑稳态误差是否满足电压精度的要求即可.

应用拉氏变换的终值定理可求出电源电压的稳态误差值，由于电源稳态精度为3%的要求，则取KP=1.13×103.

3.3.2 稳定性

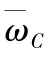
4 实验结果

加入控制环节后系统开环波特图如图2所示，其中穿越频率为1.13 Hz，相位裕量为90°，增益裕量为40 dB.从系统稳定性、稳态精度和系统抗高频干扰能力方面考虑，该设计是符合各项电源设计指标要求.

采用MATLAB 中Simulink 进行仿真响应时间与稳态时输出电压值均达到设计要求.

图2 补偿后系统开环波特图fig.2 the bold plot of compensated open loop system

图3 阶跃输入仿真图fig.3 step response simulation diagram

图4 方波输入仿真图fig.4 square－wave response simulation diagram

5 结 论

本文是在小信号分析基础上建立了开关电源数学模型，确定了相关PI 反馈控制方案，从实验结果可以看出，控制系统的各项控制参数均能满足电源精度及系统响应实时性设计要求，解决了开关电源仅靠经验设计控制参数的弊端，为今后的相关电源控制系统设计提供了理论依据和分析思路.

［1］张占松，蔡宣三.开关电源的原理与设计［M］.北京:电子工业出版社，1998.

［2］毛鸿，吴兆麟.高精度开关稳压电源的系统分析与设计［J］.电力电子技术，1999，33(2):1－4.

［3］郭唐仕，尹华杰.BUCK 变换器的数字模糊PID 控制［J］.电源技术应用，2002，5(5):181－184.

［4］朱鹏程，郭卫农，陈坚.升压斩波电路PI 和PID 调节器的优化设计［J］.电力电子技术，2001，35(4)，28－31.

［5］蔡子亮，方波.稳流型开关电源控制系统研究［J］.电力自动化设备，2007 (08):69－72.

［6］顾良翠.一种高功率开关电源控制系统［J］.高电压技术，2005 (12):35－41.