永磁无刷直流电机电感分析及优化设计

茆美琴，张邵波

（合肥工业大学 教育部光伏系统工程研究中心能源研究所，安徽 合肥230009）

近年来，随着电力电子器件的发展和永磁材料性能的不断提高、价格不断降低，使得永磁无刷直流电机（PM＿PDCM）的性能和应用领域得到前所未有的发展[1－2]。 如：在电动汽车领域和新能源领域中，由于永磁无刷直流电机具有体积小、效率高、可控性好等优点，使其成为电动汽车电机和光伏水泵中的主流电机。 在永磁无刷直流电机的换相过程中，由于电机电感的存在，使得电机电流在换相过程中会发生波动，从而引起电机转矩的波动。 对于高速运行的永磁无刷直流电机，若电机电感过大，会导致电机的换相时间在电机运行周期中占的比例过大，甚至会引起电机的换相失败。 因此，避免电机换相失败和减小电机的转矩波动对提高永磁无刷直流电机的性能具有重要意义。

目前对永磁无刷直流电机的转矩波动和换相失败进行讨论的文献大多仅限于控制视角。 文献[3]通过在线实时计算最佳超前角度来减小电机的转矩波动；文献[4]提出了基于自适应人工神经网络的换相转矩脉动的抑制方法，文献[5]提出了基于自抗扰控制器的无刷直流电机控制系统。 文献[6]提出基于直接转矩控制方式来实现转矩脉动的抑制。

本文从系统参数整体优化出发，在研究永磁无刷直流电机主要性能参数与其控制性能的关系基础上，以优化永磁无刷直流电机系统换相性能为目标，提出了永磁无刷直流电机定子电感优化设计方法，并推导出了避免电机换相失败的最大电感值和减小转矩脉动的最小电感值，从而保证永磁无刷直流电机具有良好的换相和动态性能。

1 电感对电机换相的影响分析

1.1 换相时间分析

假设在两相导通三相星形6 状态永磁无刷直流电动机中，电机处于理想换相模式，转子每转过60°（电角度）就换相一次[7]。图1给出了AC→BC 换相模式的电路图。

图1 电机换相过程示意图Fig.1 Motor phase commutation schematic

假设永磁无刷直流电机相电流的幅值为Is，反电势的幅值为E，电机在ta时刻换相结束。 由图1可知，换相前A 相和C 相电流满足：ia（0+）=-ic（0-）=Is，换相结束后B 相和C 相电流满足：ib（ta）=-ic（ta）=Is。 根据文献[8]可计算出电机换相时间为

因为电机的换相在ta时刻结束，所以在ta时刻有：

联合式（5）和式（6）可以解得电机的换相时间为

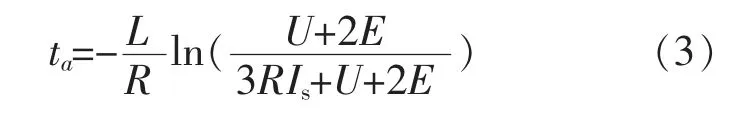
从式（3）可以看出，电机的换相时间与电机的电感成正比，电感值越大，换相时间越长。

1.2 避免换相失败的电感值分析

由于永磁无刷直流电机采用120°（电角度）导通方式则在理想情况下电机的相电流波形如图2a 所示。 电流的上升时间和下降时间均为0，电流波形呈矩形波，当每对桥臂的上桥臂导通时电流值为正且保持不变；当每相桥臂的下桥臂导通时电流值为负且保持不变。 而在实际电路中，由于绕组电感的存在，电流的上升下降时间不可能为0，实际的相电流波形如图2b 所示。 而当电机电感值很大且处于高速运行时，会出现换相绕组电流值还没有达到幅值时，电机的换相过程已经结束，电流开始下降，电流波形如图2c 所示。

图2 永磁无刷直流电机相电流波形Fig.2 PM_BDCM phase current curves

由于转子每转过60°（电角度）就换相一次，因此，若要使换相电流在换相结束前就达到稳态值，则电流的换相时间ta必须满足要求：

将式（3）带入式（4）可得：

2 电感对转矩脉动的影响分析

当永磁无刷直流电机需要调速时，往往采用PWM 调制，文献[9]论述了常用的几种调制方式，调制方式不同，对转矩脉动的抑制会产生一定的影响。 根据文献[9]可知，当电机运行在4E＞U 高速区的时候，无论采用何种PWM 调制方法，换相电磁转矩脉动均为负值，即在整个换相期间电机的平均电磁转矩将减小，这种情况下PWM调制对转矩脉动的抑制不起作用。 因此通过改变PWM 调制方式对电机的换相转矩脉动不能起到很好的作用。

下面以AB→AC 换相过程为例，分析电感值的大小对转矩脉动的影响。 根据文献[10]可知，电机的换相转矩脉动公式为

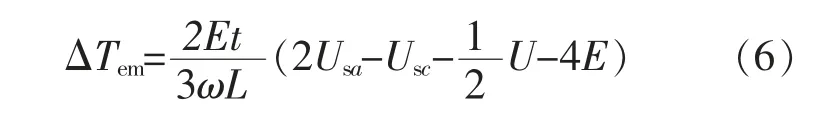
电机的额定转矩公式为

式中：Sa，Sc为A 相和C 相绕组的开关函数，开关函数为1 表示对应绕组上桥臂开关管导通，开关函数为0 表示下桥臂开关管导通；E 为电机反电势的幅值；ω 为电机机械角速度；Is为电机电流的幅值；t 为电机换相时间。

令转矩脉动△Tem小于额定转矩Tem的5%，则有：

当电机处于高速区（4E＞U）时，为了尽量减小换相转矩脉动，换相期间可以采用恒通方式，即：

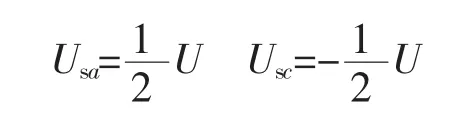
式（10）可化简为

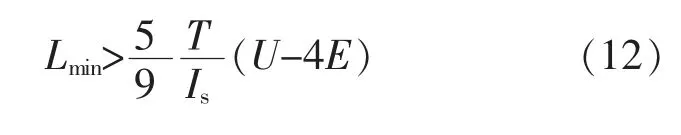
3 电感参数的优化设计

根据以上分析可知，当永磁无刷直流电机的电感值过大时会导致电机换相失败；当电感值过小时，电机的换相转矩脉动会增大。 所以永磁无刷直流电机的电感值应满足：

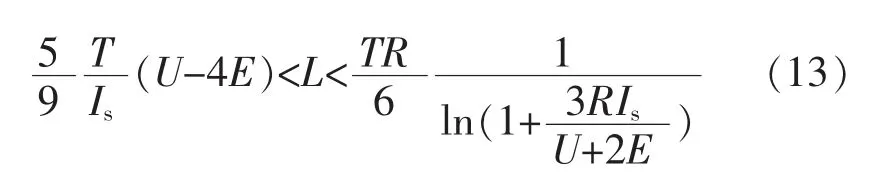
由式（13）知，绕组电感的范围既与绕组内阻、电机额定工作频率和反电势等电机结构参数的影响有关，也与控制器的直流电压和电机额定工作时绕组电流幅值等控制参数的影响有关，因此对PM_BDCM 电感参数优化设计既可从电机本体设计的角度来优化，也可从控制器的角度来优化。

在电机结构参数中，电机的极对数影响电感的范围。 根据极对数与频率的关系可知，电机的周期和极对数成反比，当极对数增加时，电感范围则减小，控制器对电感值要求则增加。 因此对于高速运行的电机，电机的极对数应尽量减小，从而提高电感范围。

在电机的结构参数中，绕组结构是影响绕组电感的主要因素。 由于分数槽集中绕组漏磁场高于分布绕组的漏磁场，电机的漏电感明显高于分布绕组的漏电感，因此分数槽集中绕组电感高于分布绕组。 电机的槽型尺寸对电机的电感也有重要影响，本文以6 极9 槽分数槽集中绕组为例，根据文献[11]的分析可知分数槽集中绕组的电感计算公式为

式中：Lslot为槽漏感；S 为电机槽数；ncond为绕组的每槽导体数；leff为电机有效轴向长度；μ0为气隙磁导率；Ws为槽体宽度；hs为槽体高度；h0为槽口高度；b0为槽口深度。

根据式（14）可知，当电机绕组参数和槽极数确定后，通过降低槽身和槽口的深度或者增加槽身和槽口的宽度可以减小绕组漏感。

综上分析，对电感参数的优化首先需要确定电感的范围，根据电感的范围设计电机，使电感值满足要求；当设计完成后，若电机实际电感超出电感范围，则可以通过调整直流电压或者改善控制方式使电感范围增大，从而使电机电感满足电感值的要求。

4 实验验证

为了验证结论的正确性，本文利用以上公式对一台6 极9 槽的永磁无刷直流电机的样机进行试验，其参数为：额定功率24 W，额定转速4 000 r/min，直流电压24 V，定子槽数9，极对数3，电阻0.45 Ω，电感4 mH，反电势9 V，周期5 ms。

样机在空载和额定负载情况下的电流波形如图3所示。 从图3a 可以看出电机在空载情况下电流幅值Is1=1.3 A，根据式（14）得出2.9 mH＜L＜9.16 mH，电机电感满足要求，所以电机电流换相正常；当电机在额定负载情况下，电流幅值Is2=4 A，根据式（5）求出1.2 mH＜L＜3.1 mH，电感值L＞Lmax2，所以电机换相失败，电流波形发生畸变。

经过优化后的电流波形如图4所示，从图4中可以看出电流幅值Is3=2 A，根据式（14）可求出1.4 mH ＜L＜5.95 mH，电机电感极限值满足要求；所以电机电流换相满足要求，不会发生换相失败。

图3 样机电流波形Fig.3 Prototype current curves

图4 优化后电机电流波形Fig.4 Optimized motor current curve

5 结论

本文在考虑电感的永磁无刷直流电机的电路模型基础上，通过分析电机电感值的大小对永磁无刷直流电机换相过程影响的分析，推导出了在避免换相失败同时又可以抑制换相转矩脉动的电感范围，并给出了优化电机电感的方法，从而为设计永磁无刷直流电机电感时提供了依据。最后通过对样机进行实验，验证了计算公式的正确性和优化方法的有效性。

[1] 唐任远．现代永磁电机设计理论与设计[M]．北京：机械工业出版社，1997.

[2] 李钟明，刘卫国．稀土永磁电机[M]．北京：国防工业出版社，1999.

[3] 刘和平，刘平，王贵.永磁无刷直流电动机换相过程分析[J].微电机，2008，41（10）：34－36.

[4] 陈冬，房建成.非理想梯形波反电势永磁无刷直流电机换相转矩脉动抑制方法[J].中国电机工程学报，2008，28（30）：18－21.

[5] Zhu Z Q，Howe D.Magnetic Field Analysis and Inductance of Brushless DC Machines with Surface-mounted Magnets and Non-overlapping Stator Winding[C]∥IEEE Trans.on Magnetics，1995，31: 2115－2118.

[6] 王超，黄运生，韩华，等.新型无刷直流电机直接转矩控制[J].电气传动，2011，41（8）：20－23.

[7] 李鲲鹏.计及绕组电感的永磁无刷直流电机电路模型及其分析[J].中国电机工程学报，2004，24（1）：10－11.

[8] 余莉，刘合祥，易龙芳.永磁无刷直流电机电路计算模型及其换相分析[J].微电机，2010，41（10）：26－27.

[9] 钟柏.无刷直流电机转矩脉动的抑制研究[D].大连：大连理工大学，2010.

[10] 任军军.永磁无刷直流电机的转矩脉动抑制的控制策略研究[D].杭州：浙江大学，2004.

[11] Ayman M,EL-Refaie.High Speed Operation of PM Magnets[D].University of Wisconsin Madison，2005.