感应电机参数静止辨识的误差特性分析

杨光，徐政，陈锐坚

（清华大学 深圳研究生院 电力系统国家重点实验室深圳研究室，广东 深圳518055）

1 引言

感应电机矢量控制系统以其良好的运行特性而得到广泛应用[1]，但是在控制算法中需要使用定／转子电阻、漏感及互感等电机参数，参数的准确与否直接影响系统的控制特性。 电机参数辨识是矢量控制变频器的基本功能之一，传统的方法基于空载和堵转试验，但是在实际应用中往往难以实施，尤其当系统安装完毕，负载不可拆卸或拆卸难度很大时，这种方法就极不适合[2]。 因此，保持电机静止状态的参数辨识方法的研究具有重要意义。 文献[3]提出了一种参数静止辨识方法和实施方案，文献[4]通过分析控制系统误差对辨识精度的影响，提出了相应的改进措施。

本文通过理论推导和仿真计算，不仅分析了变频器控制误差及检测误差对参数辨识精度的影响，而且进一步分析了控制误差、检测误差及参数误差对系统运行特性的综合影响，从而确认了实施方案的有效性，并在实际应用中取得了良好的效果。

2 参数静止辨识方法

利用变频器的输出电压控制功能与电压、电流检测功能，对电机通单相电，形成驻波磁场，保持转子静止不动，进行电机参数离线辨识。 静止状态下感应电机的T 型等效电路如图1所示。

图1 静止状态下感应电机的等效电路Fig.1 Equivalent circuit of induction motor at standstill

图1中，Rs和Rr分别为定子和转子电阻，Ls和Lr分别为定子和转子漏感，Lm为互感，为了简化，假定Ls=Lr=l。

2.1 定子电阻的辨识

采用伏安法，兼顾变频器安全和辨识精度，分别以被试电机额定电流的1/2 和1/4 作为直流电流目标值Idc，由电流反馈控制调节输出电压Udc，利用电压增量和电流增量，可较好地消除控制误差的影响，定子电阻的计算公式如下：

2.2 定子与转子漏感的辨识

采用工频加压法，以电机额定电流作为交流电流目标值，进行适当的死区时间补偿，控制输出电流的大小及波形，稳定后从输出电压过零点开始对电流信号i 进行采样，每个周期采集100组数据，基波电流的有功、无功分量及幅值可由下式求得：

将结果代入下式，即可得漏感：

式中：U 为交流电压幅值；I 为响应电流幅值；θ 为电流滞后角；ω 为电压角频率。

2.3 互感与转子电阻的辨识

采用双低频电流激励法。 等效电路端口等效电抗Z 的虚部Im（Z）为

其中 L=Lm+l τr=L/Rrσ=1-(Lm/L)2

设定输出电流的大小Iref，实施闭环控制，然后结合对应的输出电压uout（t），计算Im（Z）：

通入2 个不同频率ω1和ω2单相正弦电流激励，检测和计算对应的Im（Z1）和Im（Z2），代入式（5）即可解得Lm和Rr：取ω1=2ω2，可大大简化Lm和Rr的求解公式。

3 系统误差及其影响

3.1 系统误差分析

变频器存在控制误差和检测误差，输出电压的控制误差△U 中含有2 个分量：恒定分量△U1由死区时间、 开关器件的导通和关断延迟时间、导通压降等因素造成[5-8]，与输出电压的大小无关；比例分量△U2主要源于直流母线电压检测误差对占空比计算的影响，与输出电压的大小成正比。 电压、电流的检测误差由传感器、采样及A/D转换电路的偏差造成，由于上述电路具有足够高的响应速度，而且运行时会适时作零点校正，所以检测误差可只考虑比例分量。

3.2 对参数辨识的影响

用变频器实施上节所述参数辨识方案，其控制和检测误差必然会对辨识结果产生影响。 由于△U1很小，只有当变频器输出低压时才会产生明显影响，而定子电阻辨识已采用式（1）的电压、电流增量法，互感与转子电阻辨识中利用Im（Z）的特性，有效地消除了△U1的影响，故可只考虑输出电压和电流的比例误差对参数辨识的影响。 设电压及电流的误差比例系数kU和kI分别为

其中，带“^”的变量为含系统误差的参数辨识结果；无“^”的变量为无系统误差的理想结果。

3.3 对系统控制特性的影响

以无速度传感器转子磁场定向矢量控制系统为例，基于下列2 个方程，通过调节定子电流的d 轴和q 轴分量，分别控制输出转矩和磁链为

式中：Tem为电磁转矩；p 为电机极对数；isd，isq分别为定子电流d，q 轴分量；Ψrd为转子磁链。

磁链估算采用电压模型，在静止坐标系下，

转速估算采用参考模型自适应方法，将式（14）作为参考模型，可调模型设为

式中：Ψr为由式（13）计算得到的旋转坐标系下的转子磁链；ωr为转速。滑差ωsl由下式计算：

转速的自适应估算公式如下：

由于系统误差同时对参数辨识、状态观测和系统控制产生作用，需要进一步分析其对系统稳态和动态控制特性的综合影响。

系统误差对参数辨识的影响如式（11）所示，在状态观测环节中，将式（9）～式（11）代入式（12）、式（14）～式（16），经推导可知，输出转矩估算受控制误差和检测误差的双重影响：

磁链估算只受控制误差的影响：

而系统误差对滑差及转速估算没有影响：

其中，带“^”的变量为含系统误差的估算结果，无“^”的变量为无系统误差的理想结果。

因此，系统能够实现对转速的无稳态偏差控制，而磁链控制存在稳态偏差，磁链稳态值为

式中:Ψref为磁链目标值。

因为实际系统中输出电压控制误差不会太大，即kU接近1，所以对磁链控制的稳态特性影响并不严重。

系统的动态控制特性取决于变频器输出电压对isd和isq的控制，基于下列电压方程组，usd，usq为

其中 ωs=ωr+ωsl

由于计及系统误差对参数辨识及状态观测的综合影响，系统的电压方程组与理想系统保持完全一致，故系统的动态控制特性不会明显受系统误差的影响。

4 仿真与实验结果

对1 台4 极15 kW 感应电机矢量控制系统进行仿真验证，图2～图4为100 N·m 负载条件下调速运行的仿真结果，目标转速设为0→120→160 rad/s，磁链目标值为1.0 Wb，其中波动变化的曲线为速度和磁链的实际值，而较为光滑的曲线为对应的状态估算值。图2a～图4a 对应于无误差系统，参数辨识结果与真值、转速和磁链的估算值与实际值保持一致，控制特性良好。图2b～图4b 对应于参数误差系统，即无系统控制误差，而直接设定的控制算法中的电机参数值存在偏差，与真值之比为1.22，系统无法稳定运行。图2c～图4c 对应于控制误差系统，控制算法中的电机参数设定值与真值一致，但系统误差为kU=1.1，kI=0.9，转速与磁链有明显的偏差和波动。 图2d～图4d 对应于综合误差系统，系统误差仍为kU=1.1，kI=0.9，先进行静止参数辨识，代入控制算法，系统控制特性与理想系统相近。 表1为与图2a～图4a 及图2d～图4d 对应的参数辨识仿真结果，验证了参数辨识实施方案的有效性和理论推导的正确性。

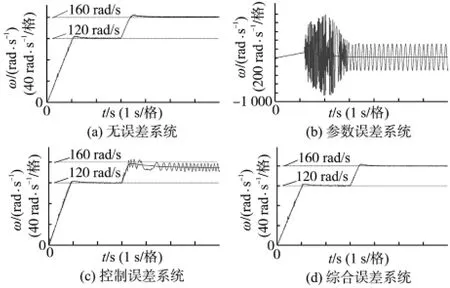
图2 转速控制特性仿真结果Fig.2 Simulation results of speed control performance

图3 磁链控制特性仿真结果Fig.3 Simulation results of flux linkage control performance

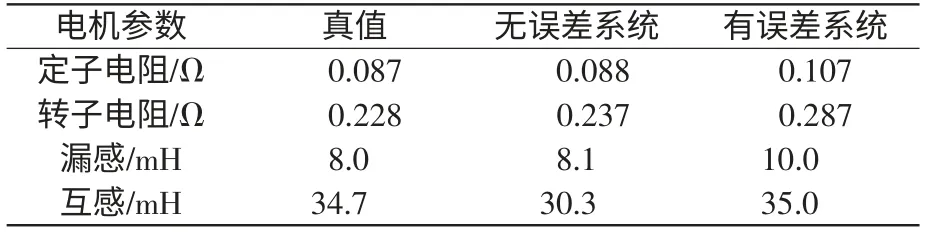
表1 参数辨识仿真结果Tab.1 Simulation results of parameter identification

进一步的仿真研究发现，如果控制算法仅按理论公式、不加任何限制条件，在图2b～图4b 系统中，只有当电机参数设定值与真值之比小于1时，系统才能够维持运行，转速与磁链有偏差和波动；在图2c～图4c 系统中，当kU/kI小于1 时，系统无法稳定运行。

将本文的静止辨识方法应用于矢量控制变频器，对不同功率等级的感应电机进行参数辨识，性能指标设定为辨识时间≤1 min，辨识偏差率≤5%，辨识变化率≤5%，实验结果如表2所示。

实验结果表明，参数辨识值稳定，满足变化率的要求，但因为未知电机参数真值，无法确认辨识偏差率，所以只能与表中通过旋转（空载和堵转）试验测得的电机参数作对比。 相对而言，采用旋转辨识方法检测转子电阻、 额定励磁电流和互感时，施加的电压高，系统误差的影响小，结果更为稳定。 尽管由于两种辨识方法采用了各自的控制设备和检测手段，造成对应的结果不完全一致，但足以验证静止辨识方法的有效性。 对表2中不同功率等级的矢量控制系统进行了全面测试，采用静止参数辨识结果，控制特性良好，完全满足设计要求。

表2 电机参数测定结果Tab.2 Experimental results of motor parameter identification

5 结论

1）为了确保良好的控制特性，电机参数自动辨识是高性能变频器必不可少的功能之一，而实现电机静止状态下的参数辨识，能够使过程大大简化和缩短，在实际应用中具有重要价值；2）基于参数静止辨识原理，结合针对应用的改进措施，静止辨识方法能够获得与常规旋转试验法同等的结果；3）变频器的控制和检测误差将导致电机参数辨识误差，但是在系统控制算法中两者的影响大部分相互抵消，仍可保证良好的控制特性。 因此，在实际应用中没有必要过于追求电机参数辨识的精度。

[1] BoseBK.ModernPowerElectronicsandACDrives[M].Harlow，En:Prentice-Hall,2002.

[2] Vas P.Parameter Estimation,Condition Monitoring and Diagnosis of Electrical Machines[M].Oxford Science Publications, 1993.

[3] 小林贵彦，金原义彦.感应电机离线参数辨识方法[J].李东钰，译.电力电子，2009（3）：9－15.

[4] 王高林，商振，于泳，等.感应电动机参数离线辨识方法实验研究[J].微电机，2009, 42（6）：4－7.

[5] 吴茂刚，赵荣祥，汤新舟.正弦和空间矢量PWM 逆变器死区效应分析与补偿[J].中国电机工程学报,2006,26（12）：101－105.

[6] Lin J K.A New Approach of Dead-time Compensation for PWM Voltage Inverters[J].IEEE Transactions on Circuits and Systems, 2002, 49（4）:476－483.

[7] Murai Y, Watanabe T, Iwasaki H.Waveform Distortion and Correction Circuit for PWM Inverters with Switching Lag-times[J].IEEE Transactions on Industry Applications, 1987, 23（5）: 881－886.

[8] Kim H S,Kim K H,Youn M J.Online Dead-time Compensation Method Based on Time Delay Control[J].IEEE Transactions on Control Systems Technology, 2003, 11（2）: 279－285.