矢量控制系统调节器设计及实验研究

沈凤龙，满永奎，王建辉，边春元，赵洪斌

（1.东北大学 信息科学与工程学院，辽宁 沈阳110004；2.辽东学院 机电学院，辽宁 丹东118001）

1 引言

三相异步电动机的矢量控制系统中，如果只对速度和磁链进行闭环控制，当速度和磁链发生突变时将引起电动机电枢电流剧增，导致变频器的逆变部分受到损坏。 同时，电流剧增还会导致转矩剧变，对传动系统造成巨大冲击[1]。这对于整个系统来说是不能允许的。 为获得良好的动静态特性，可采用电流内环和速度外环以及电流内环和磁链外环的两个双闭环控制系统。 电流内环可以保证电流的幅值和相位准确地跟踪指令值，速度和磁链外环可以保证速度和磁链的准确控制，实现无静差控制，提高系统的稳定性和抗干扰能力。 在控制系统中，双闭环通常都设计成PI 调节器的形式，使得PI 调节器的参数整定成为控制系统的关键。

在电流调节器中，由于存在着转速和转矩耦合项，使得电流调节器呈现非线性，导致转速调节器和磁链调节器的非线性。 因此，需要利用非线性系统的线性化理论，设计解耦器实现电流调节器的线性化[2－3]。 文献[4]采用一种可实现输入输出的动态解耦方法，文献[5]在此基础上引入非线性补偿来消除耦合项，实现电流环解耦。

本文首先利用三相异步电动机的数学模型，推导出矢量控制系统中电流调节器的数学模型。设计了一个解耦器解决电流调节器的耦合问题，利用工程设计方法对电流调节器的PI 参数进行整定。 将电流环作为速度调节器和磁链调节器的内环，设计速度调节器和磁链调节器并利用工程设计方法进行整定。 利用实验进行验证，实验结果充分表明控制系统具有良好的动静态特性。

2 电流调节器的数学模型及解耦器的设计

2.1 电流调节器数学模型建立

以定子电流、转子磁链和转速为状态变量的转子磁场定向的数学模型为[6]

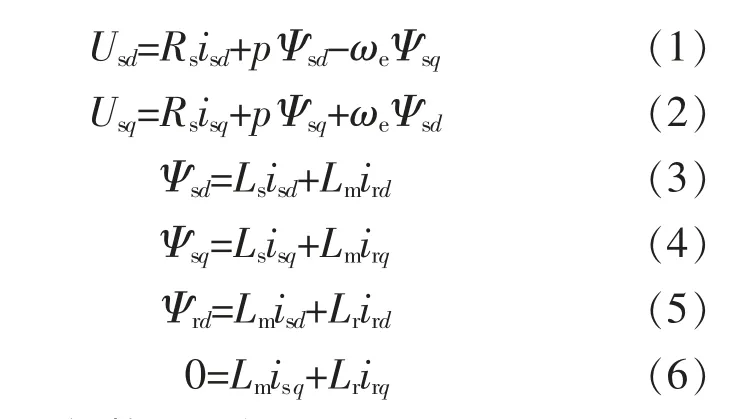
将上述方程进行整理可得：

由于电流调节过程很快，认为在电流调节期间Ψrd不变，pΨrd=0。 在电流控制器中，可以看出和电机转速相关。 同样，转矩电压也和励磁电流有关。

2.2 解耦器设计

电流调节器为非线性，需要利用非线性线性化解耦理论进行线性化处理，设计的解耦器[7]框图如图1所示。

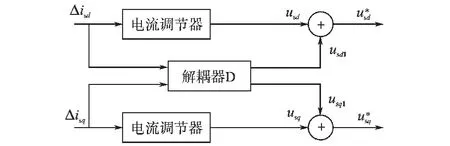
图1 解耦器结构框图Fig.1 Structure diagram of decoupling controller

根据解耦图可得：

将二者联立分别消去i*sq和isq，并令方程含i*sq和isq的项为0，得到：于是得到补偿电压如下：

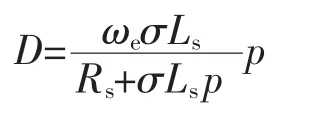
这样，就可以对电流控制器进行简化，得到电压和电流之间的传递函数

于是控制对象成为无耦合的一阶惯性环节，可以采用工程设计方法对电流控制器的PI 参数进行整定。

2.3 电流调节器参数整定

闭环调节系统由调节器和调节对象构成，调节对象有时在配上调节器后，并不能构成典型系统形式，需要对调节对象的传递函数做简化和近似处理后，才能选择适当的调节器，使整体系统构成典型Ⅰ型或Ⅱ型系统。

在三电平逆变器中，逆变器控制系统的采样是纯滞后环节，由于时间常数很小，可以将其等效成一阶惯性环节，电流检测环节也为纯滞后环节，同样可以等效成一阶惯性环节。 于是可以得到电流环的控制结构图如图2所示。

图2 电流环控制结构框图Fig.2 Structure diagram of current control loop

由图2得电流环的开环传递函数：

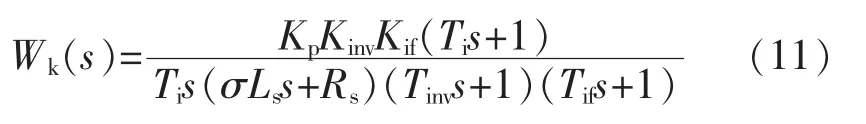
式中：Kp为PI 调节器的比例常数；Ti为PI 调节器的积分时间常数；Kinv为逆变器的实际电压和给定电压的比值，通常认为逆变器的实际电压近似等于给定电压，Kinv≈1；Tinv为逆变器的滞后时间；Kif为电流检测环节的反馈电流与检测电流的比值，Kif≈1；Tif为电流检测环节的滞后时间。

根据工程设计方法中小惯性环节的近似处理方法，令Tsf=Tif+Tinv，其中Tinv为SVPWM 算法的周期，Tif与硬件滤波电路或者软件滤波算法有关；根据零极点对消原则，设Ti=σLs/Rs，式（11）简化为

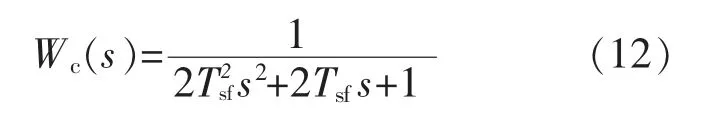
根据典型系统的工程设计方法可得：KpTsf/（σLs）=0.5 即Kp=σLs/（2Tsf）。

3 速度调节器的参数整定

在速度调节器的设计中，将电流环作为速度环的内环，需要对电流环的闭环传递函数进行进一步的化简。 整个电流环用一个时间常数为电流环等效时间常数Teq=2Tsf的小惯性环节来代替；对于速度检测环节，可以用常数为Td的一阶惯性环节表示：

这样的系统也能满足动态抗扰性能好的要求，速度环的控制结构框图如图3所示。 图3中，Kp为PI 调节器的比例常数，Ti为PI 调节器的积分时间常数。

图3 速度环控制结构框图Fig.3 Structure diagram of speed control loop

由图3得到速度环开环传递函数：

令Tn=Td+2Tsf，开环传递函数简化为

按照典型Ⅱ型系统参数关系，可以得到PI 调节器的参数为

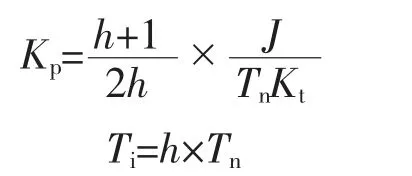
式中：h 为中频带宽，由系统的动态性能指标决定，一般选择h=5。

4 磁链调节器的参数整定

在磁链调节器的设计中，同样将电流环作为磁链环的内环，则由式（12）可得电流环闭环传递函数为

在三相异步电动机的矢量控制系统中，φrd=Lm/（1+Trp）isd，由于Tr≫Tsf，所以可将大惯性环节等效成积分环节φrd=（Lm/Tr）isd，这样，可得到磁链闭环控制结构框图如图4所示。

图4 磁链环控制结构框图Fig.4 Structure diagram of flux control loop

由图4得到磁链环的开环传递函数为

按照典型Ⅱ型系统参数关系，可以得到PI 调节器的参数为

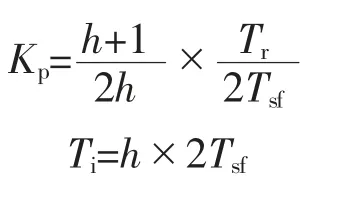
式中：h=5。

5 实验研究

搭建了如图5所示的三电平NPC 逆变器的实验平台。通过调压器可以调节三电平NPC 逆变器的直流母线电压，直流电机作为异步电机的负载电机，异步电机参数如下：额定功率为2.2 kW；额定转速为1 410 r/min；额定电压为380/660 V；额定电流为5.05/2.92 A；功率因数为0.82。 直流电机的参数：额定功率为2.2 kW；额定转速为1 500 r/min；电枢电压为220 V；电枢电流为12.5 A；励磁电压为220 V；励磁电流为0.61 A。 控制系统采用TMS320F28335DSP 芯片，SVPWM 周期Ts=0.000 5 s，直流母线电压Vdc=600 V。

图5 实验平台的结构框图Fig.5 Structure diagram of experimental platform

图6是空载启动时的电流波形； 图7和图8为电机空载稳定运行时电压和电流波形图； 图7为当电机空载运行在30 Hz 时，逆变器输出的线电压为三电平，这主要是因为控制系统输出的电压给定值U*d，U*q比较小。而如图8中，当电机空载运行在35 Hz 时输出的线电压波形为5 电平。 图9为带负载稳定运行时，突加15 N·m 的负载转矩和突减15 N·m 的负载转矩时线电压和相电流波形。

图6 空载启动过程中的电流波形Fig.6 Waveform of the current on the no-load starting

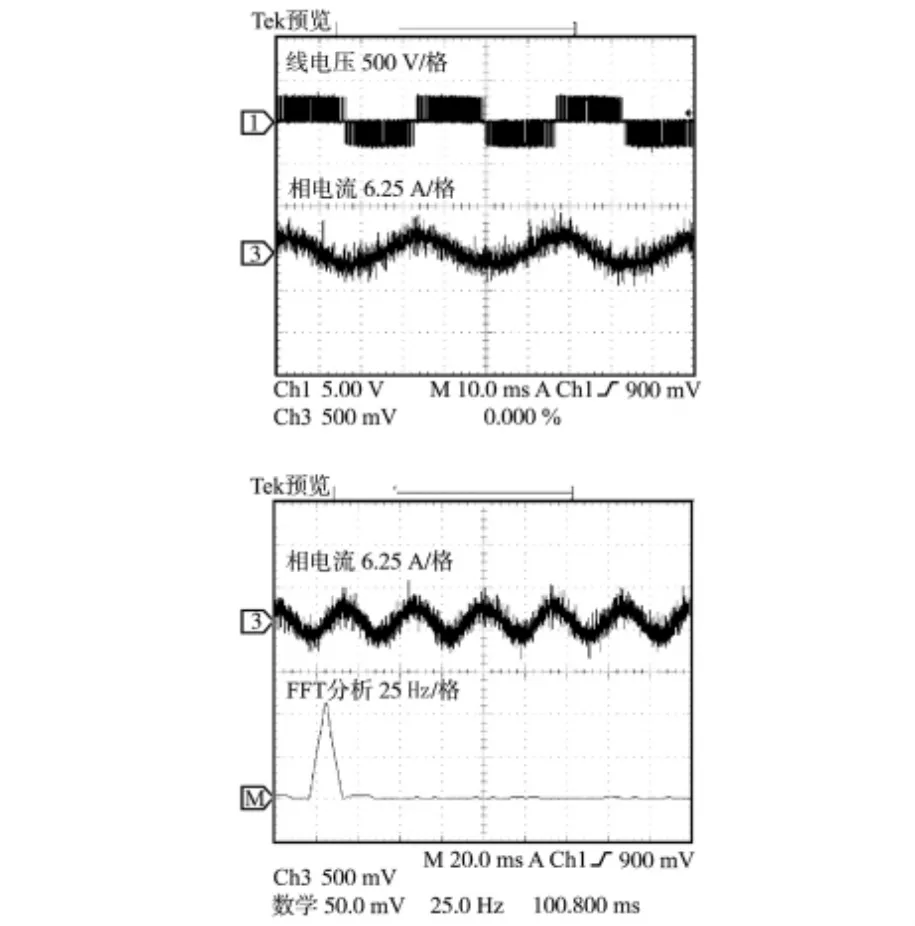
图7 30 Hz 时的电压和电流波形Fig.7 Waveforms of voltage and current on 30 Hz

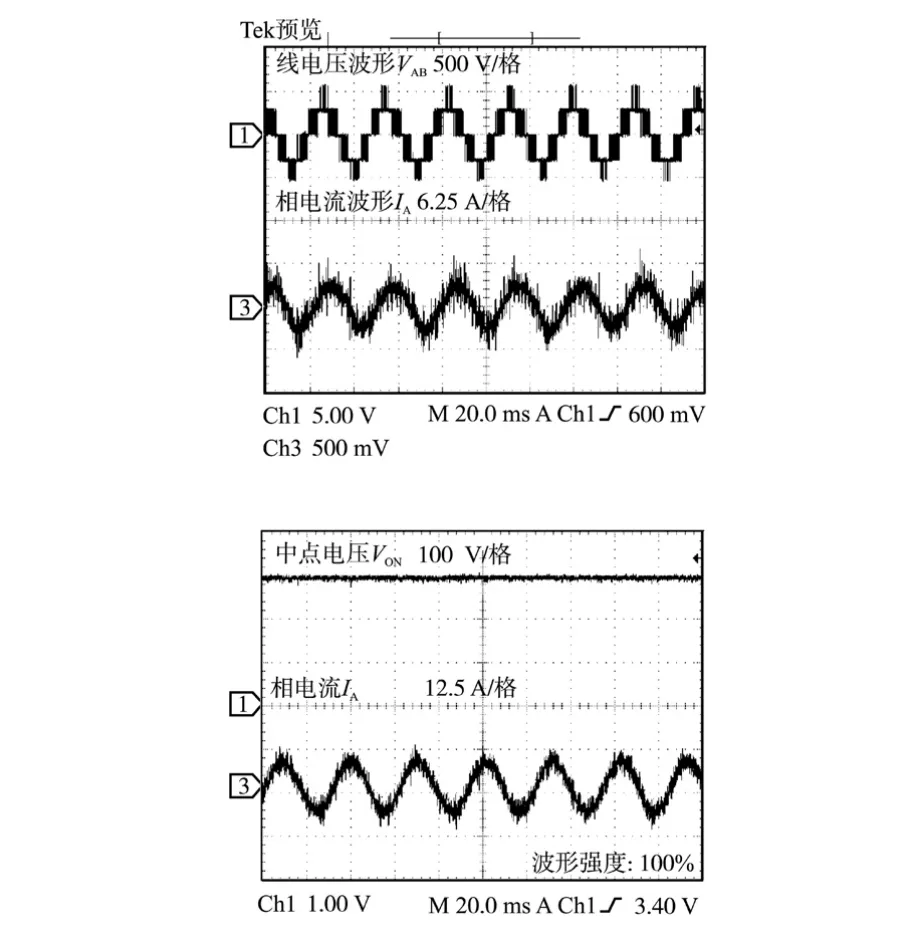
图8 35 Hz 时的电压和电流波形Fig.8 Waveforms of voltage and current on 35 Hz

图9 突加、突减负载时的电压和电流波形Fig.9 Waveforms of voltage and current when sudden increase and reduce load

6 结论

1）在分析矢量控制系统中电机模型的基础上，对电流调节器进行解耦，使解耦后的系统线性化，简化参数的整定。

2）设计电流调节器为内环和速度、磁链分别为外环的双闭环控制系统，总结了一套电流调节器、 速度调节器和磁链调节器的PI 参数整定方法，对于实验中参数调节具有重要指导作用。

3）在建立的三电平NPC 逆变器实验平台进行了空载启动、空载稳定运行、突加负载和突减负载实验，实验结果表明，基于这套参数建立的实验系统具有良好的动、静态特性。

[1] 杜永红，李哲峰，刘志刚．异步电动机间接磁场定向控制双闭环系统[J]． 电工技术学报，2009，24（5）：24－28．

[2] 马小亮．矢量控制系统的解耦与调节器设计[J]．电气传动，2009，39（1）：3－10．

[3] 祝小辉，李颖晖，付明明．永磁同步电机电流调节器动态特性及改进设计[J]． 电工电能新技术，2007，26（4）：26－30．

[4] Yoshitaka Kawabata，Tomoyuki Kamakami，Yoshiki Sasakura，et al． New Design Method of Decoupling Control System for Vector Controlled Induction Motor[J]． IEEE Trans.on Power Electronic，2004，19（1）：1－9．

[5] 李武君，阮毅，顾海强．矢量控制系统的电流解耦及其调节器设计[J]． 电机与控制应用，2008，35（12）：18－22．

[6] 陈伯时．电机拖动自动控制系统[M]．北京：机械工业出版社，2005．

[7] 周志刚.一种感应电机的解耦控制方法[J]．中国电机工程学报，2003，23（2）：121－125.

[8] Highfill G S，Halverson L A．Lowering Total Cost of Ownership with Breakthrough Magnetic Torque Transfer Technology[C]//2006 IEEE Cement Industry Technical Conference Record，Phoenix，2006：217－231．