电机控制系统低速区测速方法分析与改进

许青松 ，肖曦，王雅婷，胡丹

（1.长园深瑞继保自动化有限公司，广东 深圳518057； 2.清华大学 电机工程与应用电子技术系，北京100084； 3.三峡大学 电气与新能源学院，湖北 宜昌443000）

1 引言

现代电动伺服系统发展突飞猛进，尤其是在机械制造行业中发挥着不可替代的作用，各种机床运动部分的速度控制、 运动轨迹控制、位置控制等，大量采用了电动伺服系统[1]。在伺服等高性能电机控制系统中，速度检测环节至关重要，速度检测的快速性和精确度直接决定了整个控制系统性能[2]。 而测量转速的常用传感器一般是码盘，码盘的成本和其线数成正比，如何用低线数的码盘更快更准地测量出电机当前的转速一直是伺服测量的一个热点和难点。 利用码盘作为测量元件计算电机速度的4种方法主要有M 法、T 法、M／T 法以及变M／T法[3]。 这几种方法都是基于码盘的脉冲计时和计数进行转速计算，各有其适应的测速范围和特点。 本文首先对码盘的脉冲信号进行了仿真模拟，可以生成任意线数的编码器脉冲信号，对常规数字测速方法进行了理论分析和仿真研究，结果表明，电机处于低速情况下，上述数字测速方法难以同时满足速度的精度和动态响应，在电机处于超低速时，电机很长一段时间内检测不到编码器的脉冲信号。

为了在所有速度下（包括零速）都能获得精确的转子位置信息，一些学者提出了转子凸极追踪法[4－5]。 这种方法都是基于电机的数学模型，虽然减少了码盘的成本，但是这种方法要在同步电机定子绕组注入旋转的高频信号或者是脉动的高频信号，在伺服电机系统的应用中是不适用的。 同时另一些学者提出了速度观测器的模型，但是相比较于有码盘的测速精度，速度观测器得到的转速精度低得多。 为此，本文中将码盘信号和电机的数学模型相结合，采取插值估算的方法对电机的转速进行实时估算可以提高系统的动态响应和转速精度，同时在每次估算的基础上对电机的转速进行修正，对改进的算法进行了仿真和实验，结果表明改进算法明显提高了系统的测量精度，加快了测速的动态响应。

2 基于码盘测速方法分析对比

M 法、T 法、M/T 法以及变M/T 法测速都是基于码盘信号的处理，而码盘的线数决定码盘的价格，在实验和工程设计过程中，根据不同的电机控制系统如果要选用码盘测量转速数据可能会选择不同的码盘，高线数码盘价格昂贵，而低线数码盘无法满足精度，所以码盘线数的选择给实物电机码盘的购买和安装带来一定麻烦，本文基于Matlab 中的Simulink 模块模拟了码盘的脉冲信号，码盘信号处理流程图如图1所示，从电机系统的转速信号输入到信号的离散化，这时的离散量由电机的线数决定，然后由离散的脉冲进行正负脉冲计数后数据处理输出正交的脉冲信号，方便后面基于码盘信号处理算法的实现。

图1 码盘信号处理流程图Fig.1 Flow chart of encoder signal processing

仿真过程中，实际转速见图2a，生成的码盘信号见图2b，当电机转速为负方向时，码盘信号的B 相脉冲领先于A 相脉冲，并且相差90°，当电机转速为正方向时，码盘信号的A 相脉冲领先于B 相脉冲，并且相差90°，很好地实现了AB 脉冲信号的正交，同时可以实时修改码盘的线数，仿真操作简单，为真实的码盘测速提供了理论指导。

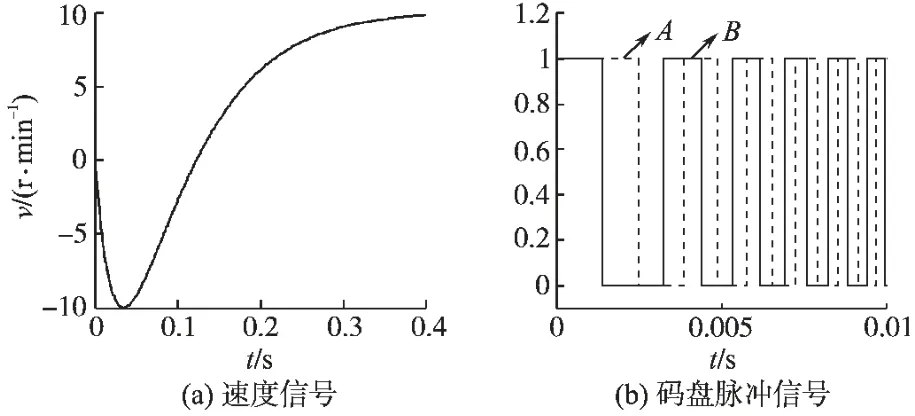
图2 速度信号和码盘信号Fig.2 Speed signal and encoder pulse signal

M 法测速分辨率与转速无关，只与码盘的线数值和检测时间有关。 欲提高M 法测速分辨率，就需要改用较大线数值的光电编码器或增加检测时间。 M 法仿真见图3a 所示，仿真速度与实际速度的误差见图3b。 从图3b 可以看出电机转速接近零时转速误差最大，误差随着转速的升高而减小，这是由于在一段时间内测量到的脉冲信号极可能不是一个整数，这时系统的测量误差就是±1 个脉冲，而在低速时测量的脉冲比高速时少，故这±1 个脉冲在低速时计算出的误差更大，理论分析和仿真分析说明M 法适合电机的高速测量，在电机处于低速时无法满足测速精度的要求。

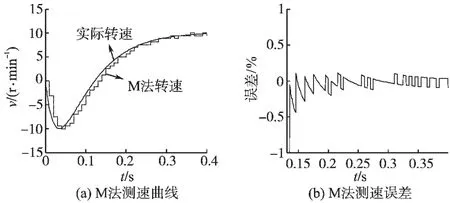
图3 M 法测速Fig.3 Speed measurement of M method

T 法仿真见图4a 所示，其与实际速度的误差见图4b，电机转速接近零时转速误差最小，虽然误差随着转速的升高而增大，但在零速附近转速的动态响应最慢，这是由于在相邻2 个脉冲信号之间的时间脉冲个数可能不是一个整数，这时系统的测量误差就是±1 个时间脉冲，而在低速时测量的脉冲比高速时多，故这±1 个脉冲在低速时计算出的误差更小，但是相邻2 个脉冲之间需要更多的时间导致系统的动态响应更慢，理论和仿真说明T 法适合电机的低速测量，但是T 法过长的延时滞后是系统不能容忍的。

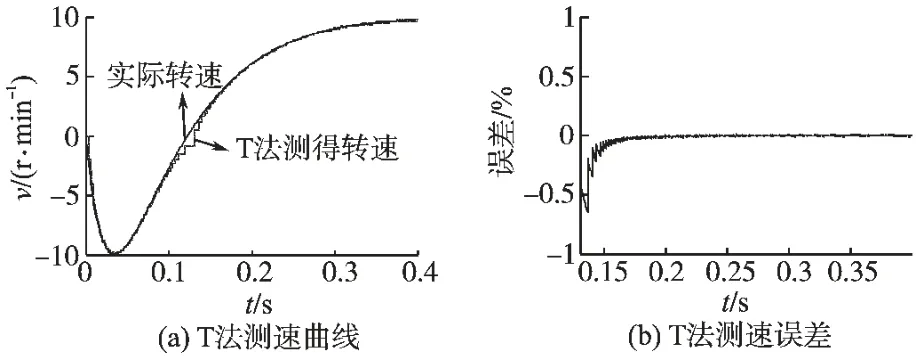
图4 T 法测速Fig.4 Speed measurement of T method

M/T 法的测速波形见图5a，M/T 法兼有M法和T 法的优点，在高速和低速段均可获得较高的精度，但是M/T 法的检测时间不能过长，否则容易引起系统的滞后。

图5 M/T 法测速和变M/T 法测速曲线Fig.5 Speed curves of M/T method and new M/T method

变M/T 法的仿真是当电机处于低速时采用T 法，即测量一个脉冲的时间来计算速度，而电机处于高速时取多个脉冲来计算，其优点是不必象M／T 法那样费力地测取△T。变M/T 法的测速波形见图5b，无论在高速或低速，其检测性能都等于或超过M 法或T 法。从图5中还可以看出，电机处于低速时电机的动态响应太慢。

4 种测速方法的仿真对比分析表明，对分辨率而言，T 法测低速时较高，随着速度的增大，分辨率变差；M 法则相反，高速时较高，随着速度的降低，分辨率变差；M/T 法的测速分辨率是常数，与速度无关，因此M/T 法比前面两种方法都好。 从测速精度上看，也以M/T 法为佳。至于检测时间，在标准的M 法中，检测时间与速度无关；在T 法中，因为取光电脉冲的间隔时间作为检测时间，因而，随着速度的增大而减小；M/T 法检测时间相对前两种方法是较长的，但是若稍微牺牲一点分辨率，可使检测时间几乎与M 法相同。 通过上面的说明，可知M/T 法在3 种测速方法中的测速精度和测速分辨率是最好的，而变M/T 法是M/T 法的改进。在电机处于高速时，变M/T 法的极限测速方法实际等效于M 法测速，在电机处于低速时，变M/T 法的极限测速方法实际等效于T 法测速，故电机处于低速时最好的测速方法其实还是T法测速，但是T 法测速的动态响应太慢，是高精度电机控制系统无法容忍的。

3 低速区测速方法的改进

当电机处于低速状态，那么从码盘信号检测到的脉冲信号时间间隔就会很长，而电机在这个脉冲间隔之间就不能获得有效的速度信息，从而使这段间隔成为反馈的盲区，电机便处于失控状态[6－8]，这在低速的高性能电机控制系统是不允许的。 为了解决这个问题，可以通过在相邻2 个脉冲信号间隔之间，隔一定的时间插入估算的速度，同时在脉冲信号到来时对估算的速度值进行修正，以提高测速系统的性能，如图6所示。

图6 改进的插值算法Fig.6 Improved interpolation algorithm

本文以永磁同步电机（PMSM）为例，其他的电机控制系统与此类似，只是电机的数学模型不同，PMSM 的机械方程如下[9－10]：

对公式进行进一步推导：

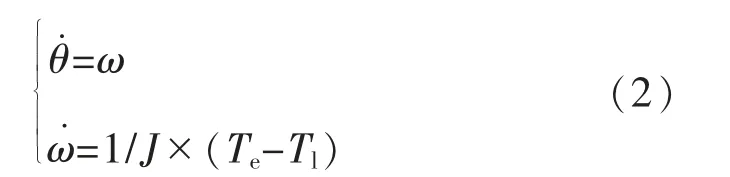
对式（2）进行离散化处理如下：

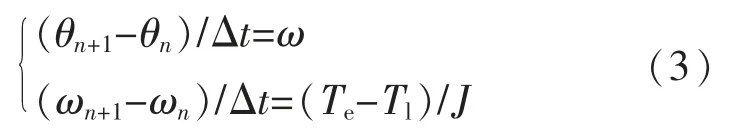
对上式进行进一步推导：

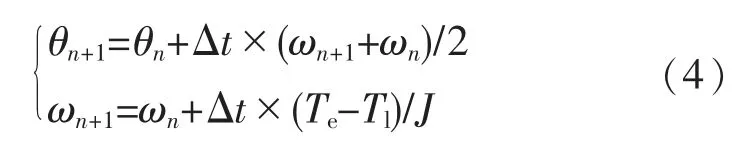
电机磁链方程如下：

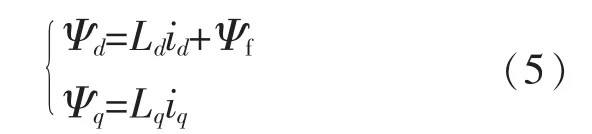
电机转矩方程：

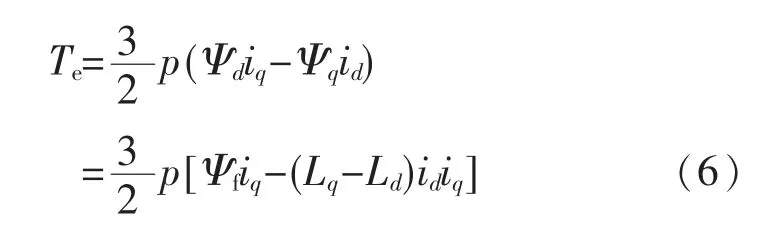
根据式（4）可以实时地插入估算的速度值，其他的变量可以实时测量得出。

这种以码盘信号和估算速度相结合的方法可以克服低速时的脉冲盲区，同时也加快了系统的动态响应，对电机的速度稳态和动态指标都有了明显的改善。

如图7a 所示，假设在新的码盘信号到来时，如果前一段时间内得估计速度有一定的偏差，那么一定会反映在估计的位置信号上。

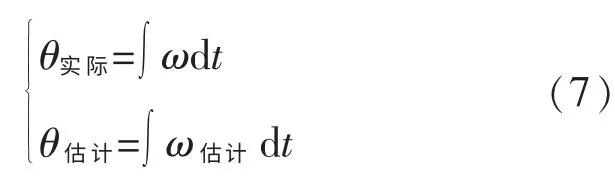
假设在很短时间内，电机的加速状态稳定，即

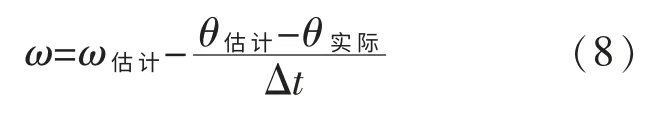
假设在上一次修正结果和实际值已经有一定的偏差，见图7b，则式（8）可以进一步修正如下式：

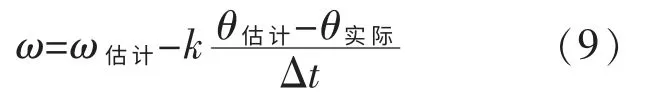
其中，k 是一个参数，它来自图中上下底的和与下底的比值，故是一个介于1 和2 之间的参数，可在实验中进行调试，其中k 与后面的乘积就是速度的修正值。

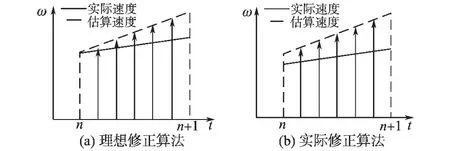
图7 修正算法Fig.7 The correction algorithm

4 仿真与实验分析

4.1 仿真验证及分析

转速仿真框图见图8，从电机输出的转速信号首先进行码盘信号处理，码盘信号处理流程图见图1，然后从这个模块输出的脉冲信号输入到转速计算，转速计算模块需要检测到电流值和电压值作为参数输入来实时进行插值，本文仿真和实验中取修正参数k=1.2。

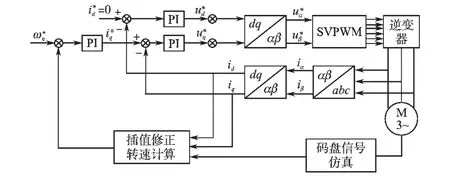
图8 系统仿真框图Fig.8 Block diagram of system simulation

图9是电机的插值估算速度测量仿真曲线和T 法的测速曲线对比，在电机处于低速时，尤其在零速附近时，T 法的动态响应慢，其原因是因为在很长一段时间内检测不到码盘的脉冲，而此时插值估算法在脉冲之间对电机的转速进行了插值，提高了测速系统的动态响应，并且插入的计算值比较接近真实的速度值，对变T 法在低速情况下的速度测量有一定的改进。

图9 插值测速曲线图Fig.9 Speed curves of interpolation method

如图10a 是插值修正测速仿真曲线，可以看出在k 取1.2 不变的情况下插值修正法很接近真实的曲线，几乎和实际转速重合，它可以在系统的每个周期进行插值和修正，比起插值估算测速法对转速性能的测量有了进一步的提升。从图10b 的误差曲线也可以看出比没有改进的误差小得多，而且在系统的每个周期都比较小，不会存在低速时检测不到脉冲的盲区。

图10 修正法测速曲线Fig.10 Speed curves of interpolation correct method

4.2 实验验证及分析

在基于TMS320F28335 DSP 的全数字化永磁同步电机伺服控制系统上，对本文提出的测速算法进行实验研究。 用于实验的永磁同步电机参数如下：额定功率=550 W，额定电流=2 066 A，最大转速=1 200 r/min，定子电阻=9.79 Ω，定子q 轴电感=36.36 mH，额定转矩=5.25 N·m，额定转速=1 000 r/min，极对数=4，定子d 轴电感=36.36 mH，转动惯量=0.000 92 kg·m2。

在给定转速为30 rad/s 的空载情况下，实验波形如图11所示，在电机空载实验时不能忽略摩擦因子带来的影响，转矩应取考虑摩擦因子的转矩数据。

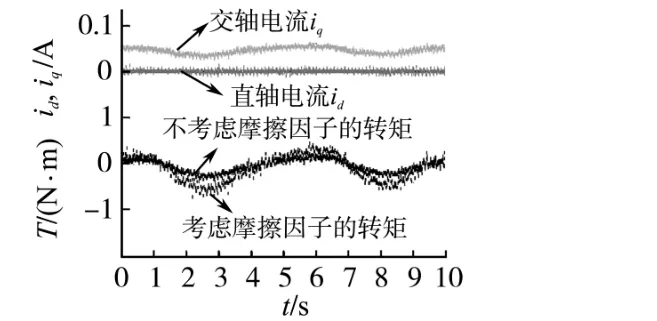
图11 id，iq，T 的实验波形Fig.11 Experimental wavaforms of id，iq，T

如图12带独立修正的波形明显比T 法测得的波形更加平滑，也更加接近真实值，尤其是在低速情况下，T 法的动态响应较慢，所以此时的转速完全是平均速度，而插值修正可以在更短的周期内插入估算的真实值，对转速的测量已经有较好的改善。

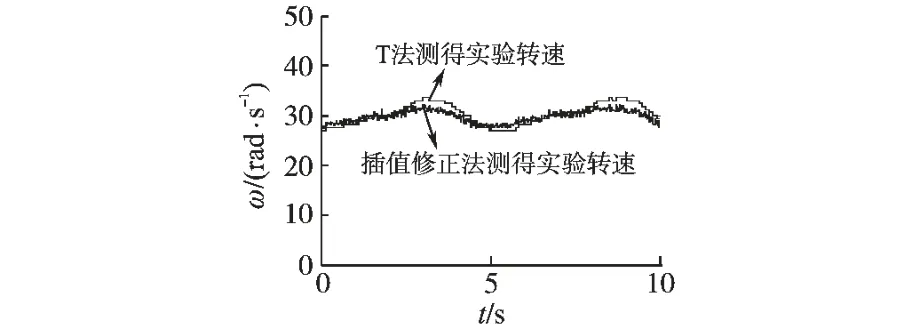
图12 实验转速波形Fig.12 Exiperimental speed wavaforms

5 结论

本文对基于码盘的4 种数字测速方法进行了系统的比较和评估，其中M 法适合高速测速，T 法适合低速测速，M/T 法和变M/T 法虽然都能满足高速和低速场合，但是在超高速场合M 法的精度最高，低速场合T 法的精度最高，然而T 法在进行超低速测速时的动态响应太慢是系统不能容忍的。 结果表明上述数字测速方法，难以同时满足电机处于低速情况下速度测量的精度和动态响应。 为此提出了基于T 法的插值估算速度测量方法，从仿真和实验可以看出，基于T 法的插值估算法对电机处于低速时的动态响应有了明显的提升，同时实时的插入瞬时值也比T 法测量的平均速度在精度上有了改善。 插值修正法可进一步提高转速测量的精度和动态响应。

[1] 张涛，杨振强，王晓旭.应用eQEP 及编码器测量电机位置与速度的方法[J].电气传动，2011，41（4）：48－51.

[2] 杨兴华，姜建国.永磁同步电机精确瞬时速度检测[J].电工技术学报，2011，26（4）：71－76.

[3] 秦晓飞，王云宽，郑军，等.交流伺服系统振动鲁棒M／T测速算法[J].电机与控制学报，2010，14（5）：97－103.

[4] 万山明，吴芳，黄声华.永磁同步电机超低速下的转速检测及控制[J].微电机，2007，40（8）：65－67，71.

[5] 钟黎萍，巩宪锋，王长松，等.零速和低速下永磁同步电机转子位置估测方法[J].电机与控制应用，2006，33（5）：33－36.

[6] Zheng Liping，Gong Xiaofeng，Wang Changsong.Rotor Position Estimation of Permanent Magnet Syachronous Motor at Zero - speed and Low - speed [J].Electric Machines and Control Application，2006，33（5）：33－36.

[7] Lee Se-Han，Ty A Lasky.Improved Velocity Estimation for Low-speed and Transient Regimes Using Low-resolution Encoders[J].IEEE／ASME Trasactions on Mechatronics，2004，9（3）:657－658.

[8] Lilit Kovudhikulrungsri.Precise Speed Estimation From a Low-resolution Encoder by Dual Sampling Rate Observer[J].IEEE／ASME Trasactions on Mechatronics，2006，11（6）：661－670.

[9] Wang Gaolin，Xu Dianguo，Yu Yong.Low Speed Control of Permanent Magnet Synchronous Motor Based on Ins -tantaneous Speed Estimation [C]∥Proceedings of the 6th World Congress on Intelligent Controland Automation，2006:8033－8036.

[10] 张绍，周波，葛红娟.于双空间矢量调制的矩阵变换器-永磁同步电机矢量控制系统[J].电工技术学报，2007，22（4）：47－52.

[11] 吴国荣，肖曦.基于自校正的伺服系统速度控制器[J].电气传动，2009，39（10）：47－50.